
 |
Heat transfer within Porous Media
Is that possible to accout for both flow and heat transfer in porous media? I have checked the ANSYS CFX manual and found that the energy equation only take the consideration of fluid (section: ANSYS CFX-Solver, Release 10.0: Theory | Basic Solver Capability Theory | Flow in Porous Media | ). I wonder how can I add the heat transfer from solid framework to fluid flow under the assumption of either thermal equilibrium or non thermal equilibrium.
|
Re: Heat transfer within Porous Media
Dear Twiti,
If you want to do the thermal equilibrium approximation, that is T_solid = T_fluid, you can "fake" the thermal conductivity within the porous domain as K = (K_fluid * Volume Porosity + K_solid * (1-Volume Porosity)) / Volume Porosity.. That should work.. For the non-thermal equilibrium, the workaround is more elaborate (via additional variables), and you should contact your CFX help desk for details.. Good luck, Opaque.. |
Re: Heat transfer within Porous Media
Yes, this is problem of CFX. I ask my frend in Moskow, and they reply to my -"It is impossible, becouse no contact access to nodal value of function". In STAR-CD this is possible.
Sorry for my english Russia, Syberia, Krasnoyarsk |
Re: Heat transfer within Porous Media
Dear Eugeny,
If your friend is interested in solving a similar problem as Twiti, and has ANSYS CFX 10.0 already, sugggest to contact the CFX help desk.. Help desk can give them a note describing how to solve this issue using Additional Variables.. Requires a bit of a variable substitution for the equations to introduce the solid properties in a fluid equation.. It has been done for steady and transient problems.. You just need to know what the ANSYS CFX solver is doing, to workaround the current limitations.. There is no need to access internal data.. Good luck, Opaque |
Re: Heat transfer within Porous Media
the solution is "Diffusive Transport Model" This equation does not compute the convective part. So the quantity is only transported by diffusion and will stay in place.
that's the way I've done: Add some additional variable(unspecified): cpSolid rhoSolid VSolid ASolid mSolid TSolid kSolid and AV specific: HSolid In Fluid Model you can define the values for individual AV eg. (all algrebaic eq): cpSolid=500[W/(m^2*K)] rhoSolid=200[kg/m^3] VSolid=0.1*Volume of Finite Volumes ASolid=200[m^2/m^3]*Volume of Finite Volumes mSolid=VSolid*rhoSolid TSolid=HSolid/(mSolid*cpSolid) cpSolid=1000[J/(kg*K)] and HSolid as Transport Equation. Kinematic Diffusity is the thermal diffusivity. But as you just want to have it in your subdomain you should define: 2e-4[m^2/s]*Subdomain, so outside the subdomain it is 0.0. You can't define Diffusive Transport in Pre, so define normal transport and edit the def-file later. the sources in your subdomain are: for the fluid kSolid*ASolid*(TSolid-Temperature)/Volume of Finite Volumes for the solid kSolid*ASolid*(Temperature-TSolid)* Density If you expect great gradients it is good to define source coefficients. that's it. bye martin |
Re: Heat transfer within Porous Media
Dear Martin,
Thanks for the hints, but this applies to the porous domain approximation via Fluid Domain plus a SubDomain.. I think that Twiti wants to use the Porous Domain as in 10.0 (this is a new feature).. Your approximation does not account for the fact that the solid matrix has a different volume than the fluid part.. Here , the solid and fluid are within the same porous domain. However, the idea is very similar but you must include the Volume Porosity in your terms.. Twiti, you can also pick it up from here.. Good luck, Opaque |
dear all.. i am facing same problem. can u please tell me how to simulate convection effect of fluid in porous media
|
Quote:
Maybe there could be a mistake in Opaque's equation. According to https://www.comsol.com/blogs/thermal...-porous-media/, the equation should read as follows: 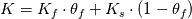 where where 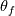 is the Volume Porosity is the Volume PorosityFurther division by 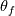 may be wrong and lead to too high equivalent thermal conductivity. may be wrong and lead to too high equivalent thermal conductivity.Edit: Please read further discussion carefully. Obviously, CFD programs differ in the way they modeling the equivalent thermal conductivity. |
I advise you to read the ANSYS CFX documentation in detail, read the statement carefully of what "fake" means, and compare the equations.
Comparing Comsol documentation vs another code w/o reading its documentation may lead you to wrong conclusions. I can still be mistaken, but I welcome you to show me where the mistake is |
Hey Opaque,
I've read through the documentations as you recommended and here is what I've found out so far: Comsol: 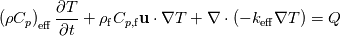 with the effective volumetric heat capacity 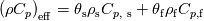 and effective thermal conductivity 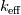 1. Volume average, which symbolically represents solid and fluid stripes in parallel to the heat flux: 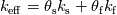 2. Reciprocal average, for solid and fluid stripes perpendicular to the heat flux: 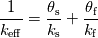 3. Power law, for a random geometry with similar thermal conductivities for the solid and fluid: 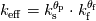 with the solid volume fraction 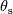 and the fluid volume fraction and the fluid volume fraction 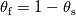 Source: https://www.comsol.com/blogs/thermal...-porous-media/ Ansys CFX: 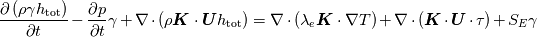 where 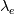 is an effective thermal conductivity and is an effective thermal conductivity and 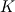 is a symmetric second rank tensor, called the area porosity tensor. is a symmetric second rank tensor, called the area porosity tensor.Ansys Fluent: ![\begin{aligned}
\frac{\partial}{\partial t}\left(\gamma \rho_{\mathrm{f}} E_{\mathrm{f}}+(1-\gamma) \rho_{\mathrm{s}} E_{\mathrm{s}}\right) &+\nabla \cdot\left(\vec{v}\left(\rho_{\mathrm{f}} E_{\mathrm{f}}+p\right)\right) \\
&=S_{\mathrm{f}}^{h}+\nabla \cdot\left[k_{\mathrm{eff}} \nabla T-\left(\sum_{i} h_{i} J_{i}\right)+(\bar{\tau} \cdot \vec{v})\right]
\end{aligned} \begin{aligned}
\frac{\partial}{\partial t}\left(\gamma \rho_{\mathrm{f}} E_{\mathrm{f}}+(1-\gamma) \rho_{\mathrm{s}} E_{\mathrm{s}}\right) &+\nabla \cdot\left(\vec{v}\left(\rho_{\mathrm{f}} E_{\mathrm{f}}+p\right)\right) \\
&=S_{\mathrm{f}}^{h}+\nabla \cdot\left[k_{\mathrm{eff}} \nabla T-\left(\sum_{i} h_{i} J_{i}\right)+(\bar{\tau} \cdot \vec{v})\right]
\end{aligned}](/Forums/vbLatex/img/7231e4e02593668a3bcee407b5004504-1.gif) The effective thermal conductivity in the porous medium, 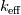 , is computed by ANSYS Fluent as the volume average of the fluid conductivity and the solid conductivity: , is computed by ANSYS Fluent as the volume average of the fluid conductivity and the solid conductivity: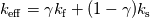 where 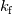 = fluid phase thermal conductivity (including the turbulent contribution, = fluid phase thermal conductivity (including the turbulent contribution, 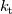 ) )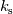 = solid medium thermal conductivity = solid medium thermal conductivitySo, if in Ansys CFX, 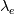 is only the sum of the molecular and the turbulent thermal conductivity of the fluid, then you might be right and introducing your "fake" thermal conductivity would lead to canceling of the porosity in the demoniator and in is only the sum of the molecular and the turbulent thermal conductivity of the fluid, then you might be right and introducing your "fake" thermal conductivity would lead to canceling of the porosity in the demoniator and in 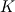 . Do you have this approach from the Ansys Help Desk? Unfortunately, there are no further information in the CFX Theory Guide than the ones I posted above. . Do you have this approach from the Ansys Help Desk? Unfortunately, there are no further information in the CFX Theory Guide than the ones I posted above. |
You got it.
For isotropic porosity (default setting), the porosity tensor is diagonal and equal to the volume porosity, Porosity * [I] No need for the help desk to confirm that. As you showed the 3 codes are using the same formulation for the diffusion term. |
| All times are GMT -4. The time now is 19:26. |