 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Lance
Join Date: Mar 2009
Posts: 669
Rep Power: 22  |
Hi,
I've read a couple of papers where people have computed the eddy-viscosity ratio and used it to motivate the use of LES in their low-Re models. For example, if the eddy-viscosity ratio becomes 0.30, some authors claim that the subgrid scale dissipates 30% of the energy of the flow, which justifies their use of LES compared to a laminar solution. Is this really true? And what happens when the eddy viscosity ratio becomes more than 1? Does that mean that the subgrid scale dissipate more energy than there is in the flow? edit: on second thought, energy is also created in the subgrid scale. Is that why the ratio can become more than 1? Last edited by Lance; September 2, 2011 at 04:36. |
|
|
|

|
|
|
|
|
#2 | ||
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
The sub grid model is not limited (in my knowledge anyway) to a ratio of 0.3. These low ratioes of dissipation simply mean the turbulence dissipation is small relative to the viscous dissipation.
I think a better way of validating an LES model is by showing that you are in the right length and time scales, or by showing that the turbulence spectrum is correct. Quote:
Quote:
By the way, for the mathematically picky - It has not been proven mathematically that the Navier Stokes equations are dissipative (ie that flow always dies out in time and does not perpetually flow). This is such a physically obvious thing but diabolical to prove formally that it has been made a millenium problem (http://www.claymath.org/millennium/N...kes_Equations/) and anybody who can prove it will be award $1 million. |
|||
|
|

|
|||
|
|
|
#3 | |
|
Senior Member
Lance
Join Date: Mar 2009
Posts: 669
Rep Power: 22  |
Quote:
I totally agree, a scale study or a turbulence spectrum would be a good way to validate the use of the LES model. That's why Im a bit confused about statements like "the eddy-viscosity ratio is 0.3, which means that the sub-grid scale dissipates 30% of the energy in the flow, which justifies the use of LES". Without a turbulence spectrum plot, is the eddy-viscosity ratio enough to motivate a (low-Re) LES simulation ? |
||
|
|

|
||
|
|
|
#4 | |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
Quote:
|
||
|
|

|
||
|
|
|
#5 |
|
Member
Mark
Join Date: Feb 2013
Location: London
Posts: 33
Rep Power: 13  |
Dear All
I have been reading very similar papers I suspect, one of them suggests that a simple grid size estimator for an LES grid would be the SGS viscosity/ molecular viscosity, you would be looking to achieve approx 20 for a high Re flow. Could this be applied to an SAS-SST model? Such as obtaining the eddy/turbulent viscosity in the fine near wall region where the SST model would have resolved the value? I can't see a way of extracting an SST specific term from Ansys CFX. I have played with extracting the kolmogorov length scale from a previous SST simulation and using that as a measure for the required transient grid length but I'm not convinced by the results although it is early days Mark |
|
|
|

|
|
|
|
|
#6 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
The Kolmogorov length scale has little relevance to a LES simulation.
The Taylor length scale is a useful starting point for working out the mesh size required for LES: http://en.wikipedia.org/wiki/Taylor_microscale |
|
|
|

|
|
|
|
|
#7 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
Energy is not created in the subgrid scale. In a turbulence model the turbulence just increases viscosity, so this is dissipative and cannot create energy -at least not in this universe, but if you can prove this you will win the $1 million Millenium prize (http://planetmath.org/millenniumproblems see number 3).
Energy can move about on the turbulence frequency spectrum, but not be generated. As I said previously the ratio being less than 1 simply means there is more viscous dissipation than turbulent dissipation. This is true for all laminar flows and turbulent flows at low Re number. There is nothing special about it. |
|
|
|

|
|
|
|
|
#8 |
|
Member
Mark
Join Date: Feb 2013
Location: London
Posts: 33
Rep Power: 13  |
Just goes to prove you shouldn't believe everything you read even if it is a journal! Hehe
Will look into the Taylor length scale Many Thanks |
|
|
|

|
|
|
|
|
#9 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
I am not saying the journal is wrong - you suggest it was saying you can estimate LES mesh size by when the viscous to turbulent dissipation ratio is one. This also sounds like a reasonable starting point for a LES mesh size. In most flows the turbulent dissipation is much bigger than the viscous, so if the ratio is 1 it means the mesh size has been reduced to the size where viscous dissipation is becoming important.
This is another independant way of estimating mesh size for LES. This is one of the really tricky things about LES. The results are dependant on mesh size and the mesh size you can use depends on the SGS model you are using. |
|
|
|

|
|
|
|
|
#10 |
|
Member
Mark
Join Date: Feb 2013
Location: London
Posts: 33
Rep Power: 13  |
Hello
Sorry for taking so long to thank you I have been chasing a bug in some simulations and hadn't got round to having a think. It had struck me that as the Kolmogorov length scale relates to the smallest features it was going in the direction of a DNS simulation hence my initial post. The results look really good, more inline with the experimental data, can i ask despite it being a slightly different subject - is there a way of exporting location settings from CFX post? I have 60 odd points/lines in a post file and I want to use them in another one, typing it in would be very dull. I export pre settings a lot as CCL files but I've never needed to do this before. Thank you again Mark |
|
|
|

|
|
|
|
|
#11 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
If you intend to do DNS style simulations you need to consider things like numerical dissipation and related issues. It is critical that the mesh defines the dissipation, not the numerics.
You can both import and export CCL in CFX-Pre and when you run the solver on the command line. In CFX-Pre you can also edit the CCL of individual objects in the tree (right click on the tree item). |
|
|
|

|
|
|
|
|
#12 | ||||
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Some interesting discussion going on here. Not an expert in this area, but would like to venture some thoughts...
Quote:
Quote:
Quote:
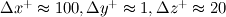 , x being streamwise direction (Ugo Piomelli, 2002). , x being streamwise direction (Ugo Piomelli, 2002).Quote:
OJ Last edited by oj.bulmer; April 17, 2013 at 00:59. Reason: Typo corrected |
|||||
|
|

|
|||||
|
|
|
#13 |
|
Member
Mark
Join Date: Feb 2013
Location: London
Posts: 33
Rep Power: 13  |
Hi OJ
Yes my venturing into the realms of Kolmogorov length scale produced some rather interesting meshes and were essentially beyond the practical computational power I had available for any reasonable time step. I'm currently attempting to emulate some experimental results for a back-step and I got some quite interesting results using the Taylor micro-scale which I calculated based on some semi-empirical formulas based on the RANS SST simulation I was using the trigger the transient simulation. The result do not however show any Brown-Roshko structures in the shear layer region between the recirculating fluid and the main flow which I was expecting to see at the Reynolds number I was considering. Clearly a bit more fiddling is need on my part! Does anyone have an opinion on what type of plot would show these structures most effectively, I was using contour plots but unsurprisingly they have a rather defined contoured nature to them which I don't think is helping. Many thanks |
|
|
|

|
|
|
|
|
#14 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
First of all, is your model sufficiently accurate that you will get the structures you expect? You will need a low dissipation numerical scheme - use the LES settings with a central differencing advection scheme. You will also need second order time stepping. Are you using these?
There are some vortex visualisation tools in CFD-Post. Have a look at the additional variables available under the puzzlingly labelled "..." button. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| LES Convergence | canopus | Main CFD Forum | 2 | December 28, 2010 07:09 |
| LES of near-laminar flows | Henrik | Main CFD Forum | 1 | June 21, 2008 18:45 |
| Laminar solver? LES? or DNS? | Ray | Main CFD Forum | 5 | March 19, 2003 10:19 |
| Turbulent viscosity | Christian Holm | Main CFD Forum | 4 | June 23, 2001 22:04 |
| ratio grid resolution (near wall/center) of dispersed bubbly flow columns using LES | Ridwan Setiadi Arrizar | Main CFD Forum | 1 | January 30, 1999 17:43 |