CFD Online Discussion Forums - modelling Differential equations in a udf

Hi!

I'm working on a CFD-model as part of my master thesis. I'm pretty alone in using CFD in my research group so i have to figure out how to do most things myself. I have good knowledge of the Ansys fluent software but I have never programmed a UDF file before and that is why I seek help here. I have articles describing all the governing equations and what methods to use but I have trouble figuring out how to translate this into a working C code.

Basically I have to implement the DQMOM-IEM model for a competitive reaction that have the following form:

$(1) A+B \rightarrow P1 \hspace{26 mm} K = 10^8 m^3/ mol s$

$(2) A + D \rightarrow A + P1 + P2 \hspace{7 mm} K = 0.67 m^3/ mol s$

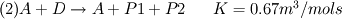
B and D are added in one inlet and A in the other. The DQMOM-IEM model will use two environments two describe the mixing of the two flows. The first reaction is treated as instantaneous and only the second have a chemical source term. The k-[math\epsilon[/math] model will be used to calculate the turbulent dissipation

I need five conserved scalars which will be implemented as user defined scalars $p_1, p_1\xi_1, p_2\xi_2, p_1Y_{21}, p_2Y_{22}$ .

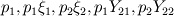
I also have five transport equations describing the mixing and reaction

Transport equation for volume fraction of environment 1

:

$\frac{\delta \rho p_1}{\delta t} + \nabla \times \rho \langle\textbf{U} \rangle p_1 = \nabla \times (\rho \varGamma_T \nabla p_1) (1)$

$\varGamma_T = \frac{C_\mu k^2}{Sc_T \epsilon} (2)$

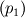
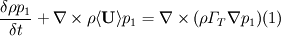
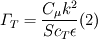
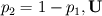
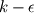
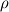
$p_2 = 1-p_1, \textbf{U}$ is the mean velocity which is together with k and $\epsilon$ given by the $k-\epsilon$ model and $\rho$ is the mean density, which is known.

The transport equations for the mixture fraction in the two environments are.

For the first environment
$\frac{\delta p_1 \xi_1}{\delta t} + \nabla \times (\langle\textbf{U} \rangle p_1 \xi_1) = \nabla \times (\varGamma_T \nabla (p_1 \xi_1)) + \gamma p_1 p_2 (\xi_2-\xi_1)$
$+ \frac{\varGamma_T}{\xi_1 - \xi_2} (p_1 |\nabla \xi_1|^2 + p_2 |\nabla \xi_2|^2) (3)$

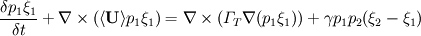
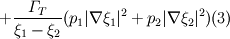
The second is very similar
$\frac{\delta p_2 \xi_2}{\delta t} + \nabla \times ( \langle\textbf{U} \rangle p_2 \xi_2) = \nabla \times ( \varGamma_T \nabla (p_2 \xi_2)) + \gamma p_1 p_2 (\xi_1-\xi_2)$
$+ \frac{ \varGamma_T}{\xi_2 - \xi_1} (p_1 |\nabla \xi_1|^2 + p_2 |\nabla \xi_2|^2) (4)$

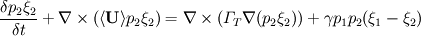
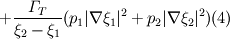
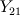
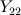
The last two equations are for the reaction transport variables, $Y_{21}$ and $Y_{22}$ . They both consider only reaction two since one is considered instantaneous.

$\frac{\delta p_1 Y_{21}}{\delta t} + \nabla \times ( \langle\textbf{U} \rangle p_1 Y_{21}) = \nabla \times ( \varGamma_T \nabla (p_1 Y_{21})) + \gamma p_1 p_2 (Y_{22}-Y_{21})$
$+ \frac{ \varGamma_T}{Y_{21}} - Y_{22} (p_1 |\nabla Y_{21}|^2 + p_2 |\nabla Y_{22}|^2) + p_1 S_{2\infty}(\xi_1, Y_{21}) (5)$

$\frac{\delta p_2 Y_{22}}{\delta t} + \nabla \times ( \langle\textbf{U} \rangle p_2 Y_{22}) = \nabla \times ( \varGamma_T \nabla (p_2 Y_{22})) + \gamma p_1 p_2 (Y_{21}-Y_{22})$
$+ \frac{\varGamma_T}{Y_{22} - Y_{21}} (p_1 |\nabla Y_{21}|^2 + p_2 |\nabla Y_{22}|^2) + p_2 S_{2\infty}(\xi_2, Y_{22}) (6)$

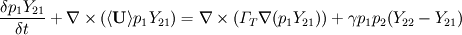
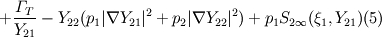
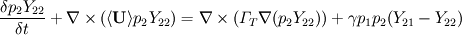
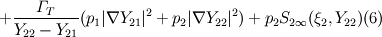
The chemical reaction source term have the following equation:

$S_{2\infty}(\xi,Y_2) = C_{B0} \xi_{s1} k_2 \times \left(\frac{1-\xi}{1-\xi_{s1}} - Y_{1 \infty}\right)\left(\frac{\xi}{\xi_{s2}} - Y_2\right) (7)$

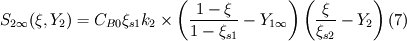
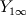
Since the first reaction is treated as instantaneous $Y_{1\infty}$ can be determined by the following formula.

$Y_{1\infty} = min\left(\frac{\xi}{\xi_{s1}},\frac{1-\xi}{1-\xi_{s1}}\right) (8)$

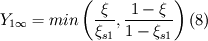
The last parts of the equations follow. This is all I should need to implement the DQMOM-IEM method in my model

$\xi_{s1} = \frac{C_{A0}}{C_{A0} + C_{B0}}, \hspace{5 mm} \xi_{S2} = \frac{C_{A0}}{C_{A0} + C_{D0}} (9)$

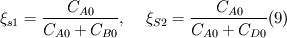
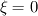
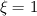
$\xi = 0$ in the stream that contains A and $\xi = 1$ . Finally the concentration on the different species in each environment (n) can be written.

$C_{An} = C_{A0}(1 - \xi_n - (1-\xi_{s1}Y_{1n})) (10)$
$C_{Bn} = C_{B0}(\xi_n - \xi_{s1}Y_{n1}) (11)$
$C_{Dn} = C_{D0}(\xi_n - \xi_{s2}Y_{2n}) (12)$

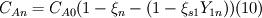
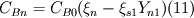
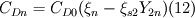
These are all the equations. It might seam much but they are all very similar to each other. According to the article i got this from the solution can be divided into three steps

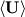
(1) Solving the turbulence model for $\langle \textbf{U}\rangle$ , k and $\epsilon$
(2) Solving the nonreactiong DQMOM-IEM model (in effect equations 2, 3 and 4) to find

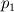
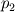
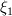
, $\xi_1$ and $\xi_2$
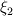
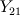
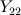
(3) Solve the reaction equations (5 and 6) to get $Y_{21}$ and $Y_{22}$ and then concentrations can be calculated with equations 10-12.

Now on to my question. I want to program these equation into a UDF-file. I know the basics behind the programming like how to import the velocity and how to extract the variables in the end. But i don't know how to go about solving these differential equations.

Should i solve them by hand and then implement the solutions into the UDF or is it possible to program a coupled UDF-solver in C, which of course would be the best option? I'm pretty sure i will experience more problem on the way but this is what i need to know before i start the programming. If anyone would be interested in coaching me a little on this problem it would be greatly appreciated, and not that it might matter that much but you would get your name on the thank you list of my master's thesis:)

I also don't know how to distinguish between the to different environments. I think i should use domains, threads and cells but if anyone have a example code used for similar cicrumstances that i could look at.

I hope i haven't forgotten any important information and that the equations are readable.
I Once again sincerely thank anyone who has any input on this problem.
Rikard Meyer Norén
Studying at ECUST, Shanghai originally from Chalmers University of Technology, Gothenburg.