 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
Hi all,
i've setup a very simple simulation: a flat terrain, with a given inlet velocity and turbulence kinetic energy profile (find it on a paper). To create these profiles, i've setup a UDF. Link to the simulation I was expecting the velocity profile to mantein along the domain length, as it was written in the paper. Instead i've found these velocity profiles (picture in the attachment: line-0 = inlet; line-1650 = outlet, ie 1.65m; line-825 = mid section, ie 0.825m). If i remove the turbulence kinetic energy profile, and set it to value 1 m^2/s^2, the velocity profiles are way better... Question is: why the turbulence kinetic energy profile is giving me those strange results? |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
Which turbulence model did you use in your simulation?
Which kind of wall function? How about Yplus values? |
|
|
|

|
|
|
|
|
#3 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
k-epsilon with enhanced wall treatment, because y+ < 1 (in this case it starts at 0.9 at inlet, and drop to 0.4 at outlet).
|
|
|
|

|
|
|
|
|
#4 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
A quick estimate of the Reynolds number yields ~1600 (assuming the kinematic viscosity of air).
Are you sure that this is correct? If so, the standard k-epsilon model is not the best choice because of the relatively low Reynolds number. Did you try other turbulence models? |
|
|
|

|
|
|
|
|
#5 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
all the data used in the simulation are taken from the paper, and i'm pretty sure to have them extracted correctly.
i know k-epsilon is not the best choice for low Reynolds number. Still i'm using it because it gives me the best result. The paper i'm following is: "Near wall characterization of the flow over a two-dimensional steep smooth hill" by J. B. R. Loureiro, F. T. Pinho, A. P. Silva Freire. It discuss about the experimental data of a flow over a hill. I have setup the hill simulation, with the same inlet profiles (extracted from the paper). The results of the hill simulation were not satisfactory, as you can see from the following pictures (i can't use the attachment because the quality of the pic would be too low...): Velocity Profiles; Turbulent Kinetic Energy Profiles; Domain of the simulation; y+ plot Where: H=60mm (height of the hill); u_delta=0.0482 m/s (external velocity/free stream velocity). As you can see from the velocity profiles image, even at x/H=-5 (at the base of the uphill) there are significant variation from the simulation data and the experimental data. Besides, you can see the k-epsilon method with Enhanced Wall Treatment is working better in the recirculation region. I've decided to use this method because, given the low free stream velocity (just 0.0482 m/s), it is impossible to have y+>30. So i've setup the flat terrain simulation, with the same inlet profiles, to investigate what are the reasons of this behavior. It seems like the flow is not in fully developed state. Do you have any ideas about what can i do to improve the result? |
|
|
|

|
|
|
|
|
#6 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
What is your boundary condition for the dissipation of the tke at the inlet?
This could cause the discrepancy between the simulation and the experiment. |
|
|
|

|
|
|
|
|
#7 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
for the turbulent dissipation rate, i'm using the default value of 1m^2/s^3; the paper doesn't provide a dissipation profile.
What value should i try? |
|
|
|

|
|
|
|
|
#8 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
This seems to be too much, which would also explain why the tke in your simulations decays too fast.
Since the flow is considered fully developed, you could run a simulation with a periodic channel and take the dissipation profile from this one. Or you simply decrease it a few times by an order of magnitide until your results look better. |
|
|
|

|
|
|
|
|
#9 | ||
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
Quote:
Quote:
I was reading Fluent user guide, where i noticed the following: "The relationship between the turbulent kinetic energy, k, and turbulence intensity, I, is: k = 3/2 * (u_avg * I)^2 where u_avg: mean flow velocity. In the paper there was a chart of the longitudinal Reynolds stress profile, normalized in respect to u_delta^2 (u_delta: free stream velocity). To calculate the turbulent kinetic energy i have used: k = 3/2 * (u'^2/u_delta^2) * u_delta^2. The error i've committed, could it be neglectable? |
|||
|
|

|
|||
|
|
|
#10 | |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
Let me start from the beginning.
The turbulent kinetic energy k is the trace of the Reynolds stress tensor ![k=\frac{1}{2} \left[ \overline{u'u'}+\overline{v'v'}+\overline{w'w'} \right] k=\frac{1}{2} \left[ \overline{u'u'}+\overline{v'v'}+\overline{w'w'} \right]](/Forums/vbLatex/img/848eeaca457d78d4e1ab66af11c917d7-1.gif) . .So if the velocity profiles are normalized by 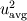 , you can recover the tke via , you can recover the tke via![k= \frac{1}{2} u^2_\text{avg} \left[ \overline{u'u'}_\text{norm}+\overline{v'v'}_\text{norm}+\overline{w'w'}_\text{norm} \right] k= \frac{1}{2} u^2_\text{avg} \left[ \overline{u'u'}_\text{norm}+\overline{v'v'}_\text{norm}+\overline{w'w'}_\text{norm} \right]](/Forums/vbLatex/img/c8a0bb9ecf69ea98237a503e0db4725a-1.gif) . .Now the way I see it, when you use 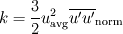 you assume that all normal Reynolds stresses are equal ( 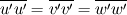 ), which is not the case for near wall turbulence. ), which is not the case for near wall turbulence.So yes, with this assumption you introduce an error which is not negligible. If the other components of the Reynolds stress tensor are given, you could use them to reconstruct the "correct" turbulent kinetic energy from the second equation. Nevertheless, if you know the individual components of the Reynolds stress tensor from the experiment, you should consider using a Reynolds stress turbulence model. Quote:
In streamwise direction between inlet and outlet, you set up a periodic boundary condition and impose a mass flow rate (with the mass flow option of the periodic boundary) that recovers the correct average velocity. This way, a profile of the dissipation of the tke develops which is in balance with the tke. You can impose it at the inlet of the actual simulation. |
||
|
|

|
||
|
|
|
#11 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
Alex, thank you for your response!
I have to take a look at Reynold Stress Model! In the meantime, i have extracted all the reynolds profiles from the paper. Just to be sure, i want to ask you this: in the attachment you can see these profiles (the circles) and the interpolations of my UDF (the green lines). My simulation is a 2D case; to calculate the turbulent kinetic energy i have used: ![k=\frac{1}{2} [ \overline{u'u'}+\overline{v'v'}] k=\frac{1}{2} [ \overline{u'u'}+\overline{v'v'}]](/Forums/vbLatex/img/cbf32d36543820e6942a3a70e5006a93-1.gif) Because the paper do not report all the values, i've done two assumptions:
As you can see from the plot, the paper reports the Reynolds shear stress profile -u'v'; fluent requires u'v'. Should i use the opposite sign profile? |
|
|
|

|
|
|
|
|
#12 | ||
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
Although your simulation is run on a 2-dimensional domain, the physics are still 3-dimensional. While the time-averaged velocity in w-direction is zero (thats why a 2-dimensional simulation with a RANS turbulence model is justified) there are fluctuations of the velocity in w-direction. Accordingly, the tke should contain all three components including 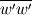 . .Edit: The sentence here made no sense at all... Quote:
Both assumptions are perfectly justified. Quote:
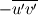 just to have less minus signs in the table, to have the plots all in the same sector of the coordinate system and to cause additional confusion just to have less minus signs in the table, to have the plots all in the same sector of the coordinate system and to cause additional confusion There is no physical difference between 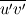 and and 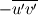 . .
Last edited by flotus1; August 12, 2013 at 08:06. |
|||
|
|

|
|||
|
|
|
#13 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
A correction to my last post. I put it in a new post so I hope you see it.
I claimed that the third component of the normal Reynolds stresses 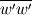 was comparatively small... Well that was complete nonsense and my only excuse is that it was late on a sunday evening. was comparatively small... Well that was complete nonsense and my only excuse is that it was late on a sunday evening.In fact, it is of similar magnitude than the second component as we can see for example from the reproduction of DNS results in Popes book (pages 13 and 14 in this document): http://pope.mae.cornell.edu/Turbulen...er7Figures.pdf If you have no data for the third component, you could estimate its magnitude from a similar figure or from a periodic channel run with a Reynolds stress turbulence model. |
|
|
|

|
|
|
|
|
#14 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
Seems like i'm having trouble to setup the periodic conditions.
I've been following fluent guide: mesh/modify-zones/make-periodic Code:
mesh/modify-zones/make-periodic
Periodic zone [()] inlet
Shadow zone [()] outlet
Rotational periodic? (if no, translational) [yes] no
Create periodic zones? [yes] yes
Auto detect translation vector? [yes] yes
|
|
|
|

|
|
|
|
|
#15 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
That is what should happen. Dont worry, you are on the right path...
With a periodic boundary condition between inlet and outlet, you cannot specify any profiles for velocity or tke in the same way you did it with the inlet boundary condition. The basic idea behind the periodic boundary conditions is to impose a mass flow rate that corresponds to the average velocity of your actual simulation. The profiles for velocity and tke (and the epsilon profile we were searching for) develop as a result of the simulation. Of course the profiles for velocity and tke wont match the profiles from the paper exactly. But it is the best estimate we have to get the profile for the dissipation of the tke (and way better than assuming a value of 1  ) )
|
|
|
|

|
|
|
|
|
#16 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
I have done some tests:
k-epsilon (standard wall function, enhanced wall treatment), k-omega, SST aren't able to converge. Reynolds Stress with enhanced wall treatment is not able to converge. Reynolds Stress with standard wall function converge. This are the results. A couple of questions: 1 - why the value of k, u'u', v'v', w'w', u'v', epsilon at z=0 is different from zero? 2 - What can be said about these profiles, in respect to the experimental data? |
|
|
|

|
|
|
|
|
#17 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
I have to make a correction to my previus post:
The result of the simulation with periodic boundary condition is shown in this image: Link 1 This results where obtained with Reynolds Stress Model with Standard wall function (I've tryed to use Enhanced wall treatment, but the simulation does not converge). I've modified the profiles of that simulation in this way: Link 2; i've used these profiles in the same flat terrain simulation, with classic boundary condition (inlet := velocity inlet, outlet := pressure-outlet). Results:
|
|
|
|

|
|
|
|
|
#18 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
I hardly believe that you cannot get a converged solution with periodic boundary conditions for the flow over a flat plate.
These cases have to converge to floating point accuracy. It may take lots of iterations though. Since you get streamwise velocity profiles of a laminar flow, the profiles for the turbulent quantities are useless too. This may happen if you initialize the periodic case with zero k, epsilon and velocity values an when the Reynolds number is low. Or when the solution is not really converged. If you tell me the Reynolds number of your case (based on the extent in wall-normal direction and the bulk velocity) I can check what is needed to obtain a suitable solution. |
|
|
|

|
|
|
|
|
#19 |
|
Member
Davide
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
Bulk velocity = 0.045920161602589 [m/s]
according to the paper: Boundary layer thickness d = 100 [mm] External velocity ud = 0.0482 [m/s] Reynolds number Rd = 4,772 Friction velocity u* = 0.0028 [m/s] Simulation with periodic boundary condition: link 1 Simulation with profiles obtained from the previus: link 2 |
|
|
|

|
|
|
|
|
#20 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,398
Rep Power: 46   |
So...
Here are the settings that definitely allow for a converged solution
The mesh consists of 50x5 quad elements with y+ around 0.7. Took around 10k iterations for the k-epsilon model to converge and 100k for the RSM model... there might be better setting to improve on this but the calculation times are low because of the small mesh. The results: velocity.pngstresses.pngdissipation.png |
|
|
|

|
|
 |
| Tags |
| turbulence kinetic energy |
| Thread Tools | Search this Thread |
| Display Modes | |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How to exclude UDFs and turbulence kinetic energy source terms? | bryanwly | Fluent UDF and Scheme Programming | 0 | May 22, 2011 13:01 |
| Mean Kinetic Energy | alastormoody11 | STAR-CCM+ | 1 | January 19, 2011 09:48 |
| LES of periodic pipe centerline turbulent kinetic energy | smehdi609 | OpenFOAM | 0 | November 30, 2010 23:59 |
| Maths problem when deriving conservation of energy equations. | Demonwolf | Main CFD Forum | 1 | June 15, 2009 14:21 |
| what's the macro of SGS turbulent kinetic energy? | lcw | FLUENT | 1 | June 13, 2006 03:08 |