CFD Online Discussion Forums - Mach-number-independence Oswatitsch

Hello,
for my studies, I've to develop a solution method for the mach-number-independence principle which is valid for very high mach-numbers. In my case I assume
- ideal gas,
- inviscid flow,
- flow over a blunt body,
- 2D flow,
- steady flow (at the end of the iteration),
- shock fitting.

In nondimensional form the systems consists of Crocco's theorem (a combination of the momentum equation and the first and second law of thermodynamics) with two equations for 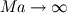${Ma\rightarrow\infty}$

${\left( {\begin{array}{*{20}{c}}u\\v\end{array}} \right)_t} = \dfrac{{1}}{{2\kappa }}\left( {1 - V^2} \right)\left( {\begin{array}{*{20}{c}}{s{_x}}\\{s{_y}}\end{array}} \right) + ({v_x} - {u_y})\left( {\begin{array}{*{20}{c}}v\\{ - u}\end{array}} \right)$

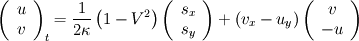
and the gas dynamic equation which is a combination of the momentum and the coninuity equation and yields for

$\begin{split} (u u_t + v v_t - \frac{1}{\rho}\frac{\kappa-1}{2}(1-V^2) \rho_t)&+ (u^2 - \frac{\kappa - 1}{2}(1-V^2))u_x + \\ (v^2 - \frac{\kappa - 1}{2}(1-V^2))v_y &+ u v (u_y + v_x) = 0 \end{split}$

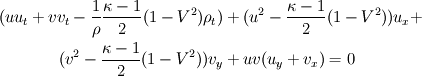
with entropy

, x-component of velocity

, y-component of velocity

, density $\rho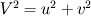$ and

with its spatial

and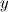

and time derivatives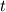

. I complement the sytems with the equation of state and the entropy equation which can be calculated in a seperate way.

I know that the system is elliptic and hyperbolic in space depending on the local velocity. So a time-dependent method must be applied. I already used MacCormack (without artificial viscosity) for a very simple case which was a 1-D streamline but the system didn't converged and became unstable. :(

Can anybody help me to find the mistake or has anybody even already implemented these equations??? :confused: