CFD Online Discussion Forums - how to calculate the viscous dissipation rate for a turbulent pipe flow

The transport equation for the mean kinetic energy reads as follows:

$0 = -\frac{\bar{u_x}}{\rho} \frac{\partial \bar{p}}{\partial x} - \frac{1}{r} \frac{\partial}{\partial r}(r \bar{u_x}\bar{u_x^\prime u_r^\prime }) + \bar{u_x^\prime u_r^\prime} \frac{\partial \bar{u_x}}{\partial r}$

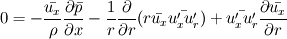
if we apply Boussinesq hypothesis, the equation can be rewritten as:

$0 = -\frac{\bar{u_x}}{\rho} \frac{\partial \bar{p}}{\partial x} + \frac{\mu_t}{r}\frac{\partial}{\partial r}(r \frac{\partial (\frac{\bar{u_x}^2}{2})}{\partial r}) - \mu_t (\frac{\partial \bar{u_x}}{\partial r})^2$

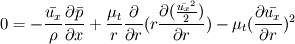
and for a turbulent pipe flow, the dissipation rate can be defined as:

$\epsilon_b = \int^{D/2}_{0}2 \pi r \epsilon(r) dr /(\pi D^2/4)$

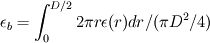
In which D is the diameter of the pipe, $\rho$ is the density of water, these parameter are known. My question is 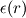$\epsilon(r)$ equals to which term in the equation, is it the last term?

and how can we compute it ?

thank you in advance,

Haoran