
 |
Quote:
what you have written corresponds to have a second derivative in time equated to zero at tn ... I don't see why to do that, you have a simply linear algebraic system to solve with a Thomas algorithm... |
Quote:
Let me put down the full equation: 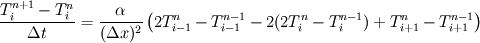 The above discretization works, but it is not any better than standard explicit discretization with regard to the time-step. |
Quote:
if you force the second derivative in time to be zero, you are supposing simply a linear behavior of T between time step tn-1 and tn+1. That means the first derivative is approximated as a constant function (first order accurate). To get higher accuracy you have to use more accurate explicit schemes... |
Quote:
When I look at the resulting difference equation it seems that for small time-steps it should correspond to standard explicit differencing, forward time centered space. |
Quote:
I am not sure to understand what you are looking for... Consider the differenzial equation: dT/dt = alpha*d^2T/dx^2 that can be integrated in time as Tn+1 - Tn = alpha* Int [tn, tn+1] d^2T/dx^2 dt The LHS can be written by means of Taylor expansion as Tn+1 - Tn = dt*|dT/dt|n + dt^2/2 * |d^2T/dt^2|n + ... Then Tn+1 - Tn = dt*alpha*|d^2T/dx^2|n + dt^2/2 * |d^2T/dt^2|n + ... Now, you can use a Lax-Wendroff type procedure: d^2T/dt^2 = d/dt (alpha*d^2T/dx^2)= alpha^2*d^4T/dx^4 This leads to a single-step second order accurate time-discretization that is explicit. Your procedure (Tn+1=2*Tn-Tn-1) is equivalent to say that (Tn+1 -2*Tn +Tn-1)/dt^2 = d^2T/dt^2 + O(dt^2) = 0 Therefore, you force that d^2T/dt^2 = O(dt^2) |
Quote:
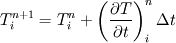 (1) (1)then approximate the 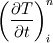 term as term as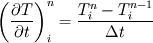 (2) (2)I don't know if this is a valid operation since we could just as well state from (1) that 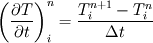 (3) (3)Anyways, (2) in (1) leads to 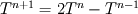 I assume that the derivatives can be written using higher order approximations as you state. |
When you start writing those finite difference equations using \approx or using \equal but including the H.O.T. you'll find the subtle difference.
Quote:
|
Quote:
Thank you. |
Quote:
I think he said that Eq.s (2) and (3) have to be written as approximation. If you use "equal to" then you have to explicitate the local truncation error, this way you will see what you are disregarding |
Quote:
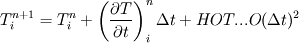 (1) (1)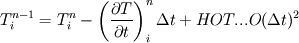 (2) (2)from (2) we get an expression 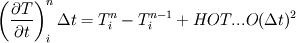 (3) (3)(3) is inserted in (1) 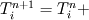 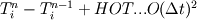 What am I supposed to see? |
|
Quote:
However, being semi-smart I realize that after three people here trying to explain the phenomena I should have got it by now. I think that I will try tomorrow when the beer from the fantastic game between Germany and Sweden wears off (guess my nationality). Also, I do get some angry comments from the beautiful woman in the next room. Why does she not understand the fun of CFD? :) |
I think I get your points now. Thank you.
For instance if I would have put 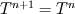 that would correspond to setting the first derivative to zero. So, is it possible to express 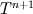 in terms of known values? in terms of known values?Edit: One more thing; It is not uncommon to extrapolate values around boundaries using mean value over the boundary (same as above essentially). 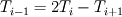 So this also forces the second (space) derivative to be zero at the boundary, correct? |
Hi, you could try a higher order discretization of your time derivative if you wish to increase time accuracy. Instead of discretizing the time derivative as:
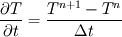 you could try 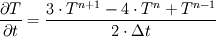 This expression is second order in time. The RHS of your equation is left untouched (fully implicit). Cheers, Michujo. P.S: I took this scheme from Versteeg&Malalasekera, 2nd Edition, page 264. |
Quote:
|
Quote:
I would rather use the above condition if the variables are given on the boundary and the computational nodes do not coincide with the boundary. Anyways, could you explain why forcing the second derivative to be zero is a bad thing in my case? Since I am not concerned with accuracy and I truncate the second derivative term, it could be "over 9000" as far as I am concerned ;) Edit: Perhaps you were referring to the zero gradient (1st order) 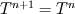 while my comment was about 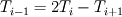 |
Hi, I did a stability analysis of your scheme (with the substitution of all the T^n+1 terms on the RHS by 2*T^n-T^n-1).
After a very long calculation I came up with the condition: 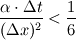 The scheme seems to be conditionally stable (as is the explicit scheme). However, the stability domain is reduced from 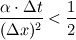 to to 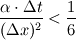 You could check this behaviour in your code. I might have made some mistakes on the way, the calculation was a bit cumbersome. In short: the trick you made does not help in the stability of the scheme, but rather it leads to a worse situation... Did it help? Cheers, Michujo. |
Quote:
Thank you this is in accordance with my own simulations (as stated in my original post). So as usual, there are no shortcuts :) |
| All times are GMT -4. The time now is 02:23. |