 |
|
|
[Sponsors] | |||||
Discretization of advection-diffusion equation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Thomas Hoffmann
Join Date: Oct 2012
Posts: 67
Rep Power: 13  |
Hi All.
My supervisor told me to write the advection-diffusion equation in discrete form. I have found it carried out in Suhas Patankars Book 'Numerical heat transfer and fluid flow', and I have attached the pages here. But I can't figure out how he integrated over the control volume and found equation (5.50). Can one of you guys show me how the terms Je, Jw, Jn and Js looks? Thanks Thomas |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi, performing the integration of the flux terms over the control volume you get:
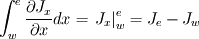 . .You just have to evaluate the flux terms at the boundaries of your control volume. So pick up expressions 5.49 (a) and (b) and evaluate them at the west. east, north and south boundaries of your cell. Does it help? Cheers. |
|
|
|

|
|
|
|
|
#3 |
|
Member
Thomas Hoffmann
Join Date: Oct 2012
Posts: 67
Rep Power: 13  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi, regarding the convective terms they are correctly formulated. For a staggered grid you have velocity directly available at the cell faces so you already know Ue and Uw. For the value of phi at the cell faces you'll have to use a discretization scheme. For instance if you use and upwind approximation phi_e will be the value of phi at the cell located left to the control cell (for positive Ue) and the value of phi at the control cell (for negative value of Ue, so flow going to the left).
The diffusive terms you wrote are wrong. You have to calculate the gradient at the cell (for example by using a centered scheme based on finite differences). The way you wrote it suggests that diffusive transport is proportional to the value of phi, whereas you know the diffusive flux is proportional to the gradient at that location, right? Also you can choose to discretize both convective and diffusive terms at once, making use of an analytical expression, by using the exponential, power law or hybrid schemes (remember this is only strictly valid for 1D problems without source terms). Anyway, all this is thoroughly described in Patankar's so you just have to look it up. Cheers. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Chris DeGroot
Join Date: Nov 2011
Location: Canada
Posts: 414
Rep Power: 17  |
||
|
|

|
|
|
|
|
#6 |
|
Member
Thomas Hoffmann
Join Date: Oct 2012
Posts: 67
Rep Power: 13  |
Thanks guys.

|
|
|
|

|
|
|
|
|
#7 |
|
New Member
tgb
Join Date: Feb 2013
Posts: 1
Rep Power: 0  |
Hi all,
I wrote code in Matlab but my advection term doesn't work. I used FDM method, could u please help me. It is said "Attempted to access q(37.95); index must be a positive integer or logical." Probably, it is a parenthesis mistake, but i can't figure out, I am stuck here. Could u please send me the original advection term for FDM? In the class, we used adv as d(uu)/dx+d(uv)/dy in the x-dir and d(vu)/dx+d(vv)/dy in y-dir. Please help!!!!!! ad(iu(i,j))=((0.5.*(q(iu(i+1,j))+q(iu(i,j))))^2-(0.5.*(q(iu(i,j))+q(iu(i-1,j))))^2)/dx ... +(0.25.*(q(iu(i,j+1))+q(iu(i,j))).*(q(iv(i,j+1)) + q(iv(i-1,j+1))) ... -0.25.*(q(iu(i,j)+q(iu(i,j-1))).*(q(iv(i,j))+q(iv(i-1,j)))))/dy; |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Chris DeGroot
Join Date: Nov 2011
Location: Canada
Posts: 414
Rep Power: 17  |
Quote:
|
||
|
|

|
||
|
|
|
#9 |
|
Senior Member
andy
Join Date: May 2009
Posts: 270
Rep Power: 17  |
Not sure if this thread is still alive but in response to the OP it is conventional to subtract phi_p * Continuity from the RHS in order for the coefficients to be in a more convenient form. Continuity of course should be zero. (Apologies if it says this in attached figure but it is too small for me to read.)
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 05:21 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 06:27 |
| Spectral Element DG and the Convection Diffusion Equation | sspatelccny | Main CFD Forum | 0 | June 30, 2012 17:35 |
| WENO Code (1D Advection Equation) | Carolyn | Main CFD Forum | 6 | March 11, 2007 13:21 |
| transport (advection) equation | DJ | Main CFD Forum | 0 | February 21, 2005 11:18 |