
 |
Roe matrix for Finite volume scheme.
Hello
From J.Blazek's, intercell flux for roe is expressed as a production of roe matrix and difference of conservation variables between left & right So, I'm trying to derive eigenvalues, eigenvectors, wave strength from roe matrix written for 2D Euler Finite volume scheme. But I confused whether I'm doing right. Many references explain the conservation lows and roe flux in serperated coordinates. From Toro, there is a method to express these flux terms as one augmented 1D flux. Where can I find a whole process to derive roe matrix for the augmented 1D flux!? Any kind of advice will be a help. Thank you in advance. |
Try to find Weiss and Smith paper "Preconditioning Applied to Variable and Constant Density Time-Accurate Flows on Unstructured Meshes".
May by it can be useful for you. |
Quote:
To find more details about Roe scheme, the chapter 11 from "Riemann Solvers and Numerical Methods for Fluid Dynamics A Practical Introduction" by Toro, E. F. will be very helpful! |
Quote:
It seems that you are trying to derive Roe matrix 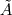 , and calculate the flux at the cell surfaces. , and calculate the flux at the cell surfaces. I did not know the details of derivation of Roe matrix 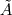 , I just used it. , I just used it. And 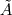 is exact the same as the original convective Jacobian A in 2D Euler equation, except that the flow variables are replaced with the Roe averaged variables (see J.Blazek's book, p108). is exact the same as the original convective Jacobian A in 2D Euler equation, except that the flow variables are replaced with the Roe averaged variables (see J.Blazek's book, p108). And the flux at the cell surface can be calculate by: 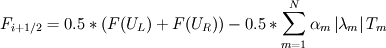 The 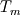 is the mth right eigenvector based on the Roe averaged matrix is the mth right eigenvector based on the Roe averaged matrix 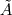 , , 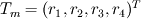 The 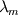 is the mth eigenvalue also based on the is the mth eigenvalue also based on the 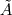 The wave strength 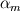 is defined by: is defined by: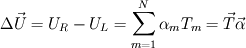 so the wave strength 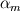 can be calculated by: can be calculated by: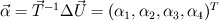 and 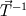 is the left eigenvector based on the is the left eigenvector based on the 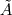 The left and right eigenvector can be find in J.Blazek's book A.11 In addition, if you just want to use Roe scheme, the Eq. 4.91-4.95 in J.Blazek's book can be used directly. I used that equations and they worked good. That is all I can do, hope that would help!:) |
inconsistent units in eigenvector matrix by Blazek or Hirsch
You mentioned the Matrix T of the right eigenvectors and the book of Blazek.
There's a big question that bothers me for years: Did somebody realize that in some components of the Matrix T in Blazek's book (formula A. 66, p. 426, 1st ed. 2001) the units are non consistent? I mean in the first three columns, rows 2 to 4, there are matrix-entries like 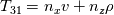 How can a quantity of units [velocity] be added to a quantity of units [density]? The same question applies to the book of Hirsch (vol. 2, formula (16.5.22), p. 181), which shows basically the same T-matrix (it's called P there and scaled by factor 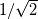 ). By the way, Hirsch is the only source where substeps for the derivation are given in addition to the resulting eigenvector matrices. Does anybody know another place where the derivation of the eigenvectors is explained step by step? ). By the way, Hirsch is the only source where substeps for the derivation are given in addition to the resulting eigenvector matrices. Does anybody know another place where the derivation of the eigenvectors is explained step by step? |
The very point on eigenvectors is that they are not uniquely determined, so different results can be obtained. The one I like more is:
Balasubramanian, Chen: Preconditioned Algorithms with a General Equation of State for Rotating Machinery Flows, AIAA 2010-4862. EDIT: I don't have confidence with those formulations showing inconsistencies, so I cannot give help on that. |
| All times are GMT -4. The time now is 18:31. |