CFD Online Discussion Forums - SPH - Finding Pressure Gradient Anywhere

Hi,

I am in need of a way to use SPH (smoothed particle hydrodynamics) to determine the pressure gradient anywhere in the fluid. That is, most of the time, you would find the pressure gradient at the center of each particle using

$\nabla P_i=-\displaystyle\sum\limits_{j=1}^{N}\frac{m_j}{\rho_j}P_j\nabla W(\mathbf{r}_i-\mathbf{r}_j,h),$

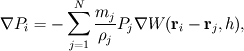
or similar, where W is typically the cubic spline kernel function. However, if you use this formula at any place outside the center of a particle, ie the space between particles, it can easily explode with very large inaccuracies unless h is very, very big, or there is a huge number of particles. I can find the density with high accuracy at any point using this technique, but not the pressure gradient.

If I knew what the pressure gradient was at each particle, I could of course do an interpolation to find the pressure gradient at locations in the spaces between the particles. But, for my current application, assume that I do not know them.

Hopefully this makes sense. Does anyone know of a way to get around this problem? Perhaps a different, more stable weighting function that would behave better?

Thanks!