 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Karthik
Join Date: May 2013
Posts: 1
Rep Power: 0  |
Hi,
I just started reading a textbook on cfd and found this statement- The computational cost for a DNS increases as the cube of the Reynold number. Can someone please explain how this order of magnitude estimate was arrived at. Thanks |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi. Imagine you want to compute the turbulent flow over a body of characteristic length
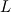 . .Suppose your mesh is uniform. Turbulence is unsteady so you will need to perform a computation over one characteristic time of the largest turbulence scale 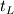 at least. Also, turbulence is 3D so the dimensions of your domain are, at least, at least. Also, turbulence is 3D so the dimensions of your domain are, at least, 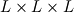 . .The minimum number of operations are the result of multiplying the number of cells by the number of time steps: 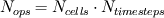 . .The Kolmogorov scale characteristic length and turnover time scale with those of the largest scale as: 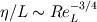 . .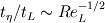 . .In a DNS you have to resolve all the turbulence scales, both in space and time. Therefore, the cell size and time step in your simulation must be 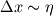 and and 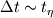 (length scale and characteristic turnover time of the smallest, i.e. Kolmogorov, scale). (length scale and characteristic turnover time of the smallest, i.e. Kolmogorov, scale).The total number of cells is therefore (notice that your domain is 3D) 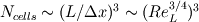 . Likewise, the number of time steps is . Likewise, the number of time steps is 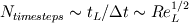 . .The total number of operations scales as 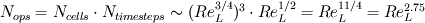 . .Notice that these are minimum requirements, so I guess you can easily reach the scaling with the third power of the Reynolds number. A detailed explanation can be found in the book of Pope. Cheers, Michujo. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
a very quick (and brutal) estimation can be done assuming that you have to work with a cell Reynolds number = O(1). Therefore, for each direction, you have
Reh = u h /ni = ReL h/L = ReL / N = O(1) |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
|
From the michujo estimate, the exact Re^3 scaling is then reached when considering an unitary Courant number (as most DNS methods rely on explicit convection schemes). As a result, the time step also scales like the grid step and the final estimate is reached.
|
|
|
|

|
|
 |
| Tags |
| dns |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Coupled solver, computational cost | Bollonga | FLUENT | 50 | July 3, 2022 10:53 |
| computational cost of ILU | Shenren_CN | Main CFD Forum | 1 | September 20, 2012 18:10 |
| URANS & SAS-SST: Computational Cost | siw | CFX | 3 | May 31, 2012 18:58 |
| Short Course: Computational Thermal Analysis | Dean S. Schrage | Main CFD Forum | 11 | September 27, 2000 17:46 |