CFD Online Discussion Forums - Boundary condition

CFD Online Discussion Forums (https://www.cfd-online.com/Forums/)

- Main CFD Forum (https://www.cfd-online.com/Forums/main/)

- - Boundary condition (https://www.cfd-online.com/Forums/main/120737-boundary-condition.html)

Boundary condition

Hi all,

I have equations to solve, which are
$\frac{\partial A}{\partial t}=\frac{\partial A}{\partial x} + \frac{\partial B}{\partial y}$
$\frac{\partial B}{\partial t} = \frac{\partial B}{\partial x}$
where

The initial conditions are zero. The boundary condition are A(x=0)=a, and B(x=0)=b. My question is do I additionally have to impose boundary condition for B(y=0)=? It seems I don't have to, is this right?

Shu

You have to set boundary conditions on all the boundaries of your domain.

Quote:

Originally Posted by shubiaohewan (Post 439532)

First, the boundary conditions must be prescribed according to the mathematical character of the system, hyperbolic and parabolic equations require BCs on open domains, only elliptic equations require to prescribe BCs on the whole frontier.

Second, I see that this is not exactly a coupled system, you can solve the second equation indipendently. Also, the equation for B does not prescribe a dependence on y.

Quote:

Originally Posted by FMDenaro (Post 439548)

Hi FMDenaro,

Thank you for your reply. I agree with your first point. I think I don't have to specify the y boundary condition for B.

The second equation will evolve by itself as you point out. But, is coupling a problem?
What about 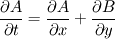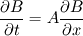$\frac{\partial A}{\partial t}=\frac{\partial A}{\partial x} + \frac{\partial B}{\partial y}$
$\frac{\partial B}{\partial t} = A\frac{\partial B}{\partial x}$

I guess I still don't have to specify the y boundary condition in B, is that? Because there is no y-direction propagation in the second equation.

Quote:

Originally Posted by shubiaohewan (Post 439749)

But this second equation is now different ...it contains A and is coupled to the first. In any case it is valid for any y...
I suggest to classify the system....

Then, at a steady state, if A <> 0 you see that B must be a function only of y, then from the first equation you have dA/dx = f(y) -> A(x,y) = f(y) (x-x0) + A0

Quote:

Originally Posted by Aeronautics El. K. (Post 439546)

You have to set boundary conditions on all the boundaries of your domain.

I would say that I agree with Aeronautics.

When you will discretize the first equation for A, you will need to know B at the boundary since you have the operator dB/dy involved in the equation. However if you use left sided FD scheme instead of central scheme you could avoid to specify B on the boundary.
Indeed you don't have y propagation of B in the B equation, but you have it on the A equation. So everything will depend on the scheme you use to discretize dB/dy in the A equation.