 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
David
Join Date: Nov 2014
Posts: 2
Rep Power: 0  |
Dear Forum members,
I recently begun to learn about basic Finite Volume method, and I am trying to apply the method to solve the following 2D continuity equation on the cartesian grid ![[0,1] [0,1]](/Forums/vbLatex/img/ccfcd347d0bf65dc77afe01a3306a96b-1.gif) x x ![[0,1] [0,1]](/Forums/vbLatex/img/ccfcd347d0bf65dc77afe01a3306a96b-1.gif) 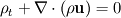 with initial condition with initial condition 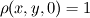 For simplicity and interest, I take 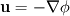 , where , where  is the distance function given by is the distance function given by 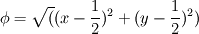 so that all the density is concentrated near the point so that all the density is concentrated near the point 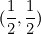 after sufficiently long enough time. after sufficiently long enough time.To solve this problem using the Finite Volume Method, I have written the matlab code (with uniform grid in x and y). Code:
% Create Grid and number of cells
a = 0;
b = 1;
N = 10;
% Define edges
x_edges = linspace(a,b,N+1);
y_edges = linspace(a,b,N+1);
%Define distance between edges
delta_x = x_edges(2) - x_edges(1);
delta_y = y_edges(2) - y_edges(1);
%Define cell centers
x_centers = a+delta_x/2 : delta_x : b;
y_centers = a+delta_y/2 : delta_y : b;
[X,Y] = meshgrid(x_centers,y_centers); % 2d arrays of x,y center values
X = X'; % transpose so that X(i,j),Y(i,j) are
Y = Y'; % (i,j) cell.
%Initialize solution array
U = zeros(N,N);
% Fill the solution array with initial data
U = X*0+1;
%define distance function
phi = sqrt((X-1/2).^2+(Y-1/2).^2);
gradphix = (X-1/2)./phi;
gradphiy = (Y-1/2)./phi;
% %reverse sign so that the gradient points inwards
v1 = -gradphix;
v2 = -gradphiy;
%Define timestep
delta_t = 0.001;
F = v1.*U;
G = v2.*U;
%Store initial data for later use
ic = U;
timesteps = 20;
for k = 1:timesteps
for j = 1:N % denote row position
%denote column position
for i = 1:N
%Top row
if (j ==N)
%Down flux
G_down = (1/delta_y)*(G(i,j)-G(i,j-1));
%Nothing is coming down from above
G_up = 0;
%Bottom row
elseif (j == 1)
%Nothing is coming in from below
G_down = 0;
%Up flux
G_up = (1/delta_y)*(G(i,j+1)-G(i,j));
%Rows in the middle
else
G_up = (1/delta_y)*(G(i,j+1)-G(i,j));
G_down = (1/delta_y)*(G(i,j)-G(i,j-1));
end
%Sideway fluxes
if i == 1
F_left = 0;
F_right = (1/delta_x)*(F(i+1,j)-F(i,j));
elseif i == N
F_left = (1/delta_x)*(F(i,j)-F(i-1,j));
F_right = 0;
else
F_right = (1/delta_x)*(F(i+1,j)-F(i,j));
F_left = (1/delta_x)*(F(i,j)-F(i-1,j));
end
Unew(i,j) = U(i,j) - (delta_t)*(F_right-F_left)-(delta_t)*(G_up - ...
G_down);
end
end
U = Unew;
surf(X,Y,Unew)
pause(0.1);
end
My code does not do its job, and I believe that there is something wrong with how I calculate my Fluxes through the four sides of my rectangular cell. ( F_right,F_left,G_up,G_down), and how I update my cell average after 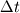 . .Could anyone give me some help? I have spent the last two weeks working on this problem, but I am still stuck and do not know how to fix it Also, is there a way to get rid of for-loops in my code? My apologies if my question is too elementary for this forum! |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Md. Intishar Rahman
Join Date: Nov 2014
Location: Bangladesh
Posts: 6
Rep Power: 11  |
Hello coagmento,
I have been working on developing a k-epsilon tubulence model in MatLab. Though my model has not been yet completed, I would like to know more more about your works. Can we talk more about this topic?  My email address is : intishar.rahman@gmail.com |
|
|
|

|
|
|
|
|
#3 |
|
New Member
mgedwards
Join Date: Aug 2015
Posts: 2
Rep Power: 0  |
% From Michael
% 1)Your main error is the flux ! see below and compare % 2) Secondly use reflection b.c.'s. % 3) The scheme below is actually FTCS which is unstable for convection % alone !!! so beware... % Let me know ! what you is your project ? % Create Grid and number of cells a = 0; b = 1; N = 40; % Define edges x_edges = linspace(a,b,N+1); y_edges = linspace(a,b,N+1); %Define distance between edges delta_x = x_edges(2) - x_edges(1); delta_y = y_edges(2) - y_edges(1); %Define cell centers x_centers = a+delta_x/2 : delta_x : b; y_centers = a+delta_y/2 : delta_y : b; [X,Y] = meshgrid(x_centers,y_centers); % 2d arrays of x,y center values X = X'; % transpose so that X(i,j),Y(i,j) are Y = Y'; % (i,j) cell. %Initialize solution array U = zeros(N,N); Unew = zeros(N,N); % Fill the solution array with initial data U = X*0+1; %define distance function phi = sqrt((X-1/2).^2+(Y-1/2).^2); gradphix = (X-1/2)./phi; gradphiy = (Y-1/2)./phi; % %reverse sign so that the gradient points inwards v1 = -gradphix; v2 = -gradphiy; %Define timestep delta_t = 0.001; F = v1.*U; G = v2.*U; %Store initial data for later use ic = U; timesteps = 20; for k = 1:timesteps for j = 1:N % denote row position %denote column position for i = 1:N %Top row if (j ==N) %Down flux G_down = (1/delta_y)*0.5*(G(i,j)+G(i,j-1)); %Nothing is coming down from above % G_up = 0; G_up = G_down; %Bottom row elseif (j == 1) %Nothing is coming in from below % G_down = 0; %Up flux G_up = (1/delta_y)*0.5*(G(i,j+1)+G(i,j)); G_down =G_up; %Rows in the middle else G_up = (1/delta_y)*0.5*(G(i,j+1)+G(i,j)); G_down = (1/delta_y)*0.5*(G(i,j)+G(i,j-1)); end %Sideway fluxes if i == 1 % F_left = 0; F_right = (1/delta_x)*0.5*(F(i+1,j)+F(i,j)); F_left =F_right; elseif i == N F_left = (1/delta_x)*0.5*(F(i,j)+F(i-1,j)); % F_right = 0; F_right =F_left; else F_right = (1/delta_x)*0.5*(F(i+1,j)+F(i,j)); F_left = (1/delta_x)*0.5*(F(i,j)+F(i-1,j)); end Unew(i,j) = U(i,j) - (delta_t)*(F_right-F_left)-(delta_t)*(G_up - ... G_down); end end U = Unew; surf(X,Y,Unew) pause(0.1); end |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Join Date: Mar 2016
Posts: 2
Rep Power: 0  |
I am writing the code of Roe linearization for Shallow water equation.
I don't know how to implement it in matlab. Is it possible to help me with that? Thank you. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
leonard Isaac
Join Date: Mar 2016
Posts: 1
Rep Power: 0  |
I am trying to write a Matlab program for a 1D unsteady conduction equation(parabolic pde).
i used finite volume method explicit scheme to solve the problem for a time=t+1. I need idea on a Matlab code that would provide future iterations. i am new to this field. \thanks. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Okay
Join Date: Oct 2022
Posts: 1
Rep Power: 0  |
Hi everyone
I am phd student, and i am stuck in bulding the program for simulation of the coaxial ground heat exchanger,i need some help in defining the programme skull,i will appreciate any help thank you all. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| my new matlab code | houkensjtu | Main CFD Forum | 3 | July 1, 2016 16:28 |
| alphaEqn.H in twoPhaseEulerFoam | cheng1988sjtu | OpenFOAM Bugs | 15 | May 1, 2016 16:12 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 02:53 |
| Can anyone help locating an error in my 2-D MATLAB SIMPLE code? | Hoggs17 | Main CFD Forum | 7 | July 9, 2013 03:02 |
| [blockMesh] Axisymmetrical mesh | Rasmus Gjesing (Gjesing) | OpenFOAM Meshing & Mesh Conversion | 10 | April 2, 2007 14:00 |