 |
|
|
[Sponsors] | |||||
Velocity distribution function sampling issue in DSMC |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,399
Rep Power: 46   |
This is rather a mathematical question:
When sampling velocity distribution functions in in a Direct Simulation Monte Carlo (DSMC) we first have to choose a small velocity interval 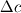 . .Now during the sampling process, all molecules with velocities between 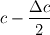 and and 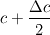 are counted with a velocity of  . .So after the simulation instead of the values of the distribution function for a certain velocity 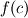 we actually get the mean value over the velocity interval we actually get the mean value over the velocity interval 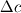 : :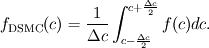 Now here is the question since this sampling method is only second order accurate in 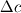 . .Is there a way to get a better approximation for the actual value of the velocity distribution function of the velocity 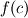 ? ?I mean a other than reducing the velocity interval 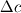 which would result in a higher amount of statistical scatter. which would result in a higher amount of statistical scatter.Maybe by using the neighbor values 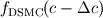 and and 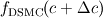 ? ?Edit: Nevermind, I found a solution that results in a fourth order accurate interpolation of the velocity distribution function. As soon as I get gnuplot to plot my results I will post the procedure here. Last edited by flotus1; December 12, 2014 at 12:42. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Quote:
Hello, I am not sure to get correctly your question but the average value when c is centered between +dc and -dc is a second order approximation of the pointwise value. It is similar to what happens in FVM. Higher order approximations require suitable reconstruction/deconvolution techniques |
|
|
|

|
|
|
|
|
#3 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,399
Rep Power: 46   |
You are right, I tend to confuse orders of accuracy.
The thing is that for the purpose of the simulation involved, the second order accurate approximation was not accurate enough. If the remedy is so obvious I will rather not post my solution because I feel like I reinvented the wheel now. |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Quote:
A way can be developing in Taylor series the pointwise function and integrate each terms. |
||
|
|

|
||
|
|
|
#5 |
|
Super Moderator
Alex
Join Date: Jun 2012
Location: Germany
Posts: 3,399
Rep Power: 46   |
For the sake of completeness, here is what I did.
The sampled DSMC value equals the following integral: ![f_\text{DSMC}(c) = \frac{1}{\Delta c} \int_{c - \frac{\Delta c}{2}}^{c + \frac{\Delta c}{2}} f(c) dc = \frac{1}{\Delta c} \left[ F\left(c+\frac{\Delta c}{2} \right) + F \left( c-\frac{\Delta c}{2} \right) \right]. f_\text{DSMC}(c) = \frac{1}{\Delta c} \int_{c - \frac{\Delta c}{2}}^{c + \frac{\Delta c}{2}} f(c) dc = \frac{1}{\Delta c} \left[ F\left(c+\frac{\Delta c}{2} \right) + F \left( c-\frac{\Delta c}{2} \right) \right].](/Forums/vbLatex/img/07db29d31a133ff74627702797a7751e-1.gif) The sum of this value and its two neighbors is 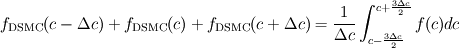 ![= \frac{1}{\Delta c} \left[ F \left( c+\frac{3 \Delta c}{2} \right) + F \left( c-\frac{3 \Delta c}{2} \right) \right]. = \frac{1}{\Delta c} \left[ F \left( c+\frac{3 \Delta c}{2} \right) + F \left( c-\frac{3 \Delta c}{2} \right) \right].](/Forums/vbLatex/img/a93e0f44e6d0ab408fc1d4b9866e2055-1.gif) Using a 4th order central difference formula for the first derivative we can reconstruct the value of 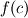 : :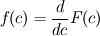 ![= \frac{1}{\Delta c} \left[ \frac{1}{24}F \left( c-\frac{3 \Delta c}{2} \right) - \frac{9}{8}F \left( c-\frac{\Delta c}{2} \right) + \frac{9}{8}F \left( c+\frac{\Delta c}{2} \right) - \frac{1}{24}F \left( c+\frac{3 \Delta c}{2} \right) \right] = \frac{1}{\Delta c} \left[ \frac{1}{24}F \left( c-\frac{3 \Delta c}{2} \right) - \frac{9}{8}F \left( c-\frac{\Delta c}{2} \right) + \frac{9}{8}F \left( c+\frac{\Delta c}{2} \right) - \frac{1}{24}F \left( c+\frac{3 \Delta c}{2} \right) \right]](/Forums/vbLatex/img/6f1ae3f0519f84eacab982ed7ea5270c-1.gif) 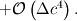 Here we can substitute the DSMC values: ![f(c) = \frac{d}{dc} F(c) = -\frac{1}{24} \left[ f_\text{DSMC}(c-\Delta c) + f_\text{DSMC}(c) + f_\text{DSMC}(c+\Delta c) \right] + \frac{9}{8} f_\text{DSMC}(c) f(c) = \frac{d}{dc} F(c) = -\frac{1}{24} \left[ f_\text{DSMC}(c-\Delta c) + f_\text{DSMC}(c) + f_\text{DSMC}(c+\Delta c) \right] + \frac{9}{8} f_\text{DSMC}(c)](/Forums/vbLatex/img/e49befe717f291c24918ba414b93f048-1.gif) 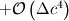 which results in ![f(c) = \frac{d}{dc} F(c) = -\frac{1}{24} \left[ f_\text{DSMC}(c-\Delta c) + f_\text{DSMC}(c+\Delta c) \right] + \frac{13}{12} f_\text{DSMC}(c) f(c) = \frac{d}{dc} F(c) = -\frac{1}{24} \left[ f_\text{DSMC}(c-\Delta c) + f_\text{DSMC}(c+\Delta c) \right] + \frac{13}{12} f_\text{DSMC}(c)](/Forums/vbLatex/img/2586d6fea3f829d8219f2f75e4608930-1.gif) 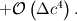 This does exactly what I want and effectively removes the sampling bias I observed in the simulations. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
If I understand, you are using reconstruction via primitive function, something like the reconstruction used in the ENO/WENO scheme.
You can also proceed this way: f(c) = f(0) + f'(0)*c + f''(0)*c^/2 + f'''(0)*c^3/6 + .... Then, integrate analytically each terms between +Deltac/2 and -Deltac/2. You see that terms like c, c^3 produce zero value of the integral. This way you have a relation between the average value (LHS) and pointwise values (RHS). You can truncate at suitable order that you need |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
PS: of course, I suppose that f is a continuous function of c, having all regular derivatives .....
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [snappyHexMesh] How to define to right point for locationInMesh | Mirage12 | OpenFOAM Meshing & Mesh Conversion | 7 | March 13, 2016 14:07 |
| get velocity gradient with a boundary function | Chris Lucas | OpenFOAM Programming & Development | 4 | August 27, 2012 03:11 |
| Moving Mesh Velocity Issue: Mesh velocity does not equal displacement | Doginal | CFX | 2 | September 8, 2011 12:02 |
| channelFoam for a 3D pipe | AlmostSurelyRob | OpenFOAM | 3 | June 24, 2011 13:06 |
| [blockMesh] BlockMesh FOAM warning | gaottino | OpenFOAM Meshing & Mesh Conversion | 7 | July 19, 2010 14:11 |