
 |
Pressure enigma.
Hey,
1. What is the physical interpretation of the pressure in an incompressible fluid? 2. It seems to me that if we are solving the momentum equations explicitly in an incompressible fluid, then we use the pressure-velocity coupling to ensure that we actually are solving the problem implicitly (which sounds correct). Do we actually need the pressure to make this implicit coupling of the velocities in the domain? |
Re: Pressure enigma.
There's always the option of using the sream function / vorticity formulation (for 1 or 2-d problems with constant viscosity). An extension of that with further manipulation gives a biharmonic equation for the stream function alone (with the same restrictions).
In either case the pressure is eliminated from the calculation - although a pressure field can be retrieved from the stream function solution. |
Re: Pressure enigma.
the disavantages of stream function vorticity include, but not limited to:
6 components in 3d, while 4 components in 3d for velocity-pressure; vorticty is the derivative of velocity, so it demands more smoothness |
Re: Pressure enigma.
physical interpretation of the pressure in incompressible flows?
pressure is just the pressure, the normal-direction force per area acting on the surfaces you are interested in. nothing fancy for the pressure in incompressible flows, in terms of concept. however, the propagation of the pressure in the incompressible flows is at an infinite speed. when you want to consider the hydroacoutsics, this is not the case (the speed of sound in water is more than 1000m/s, i don't remember exactly), but otherwise it is. in air, the propagation of pressure is the speed of the sound in air. that "the pressure progagate at infinite speed" equates a tiny chnage in the density can have a consequence of big change in pressure field. this is called stiffness. i don't understand your second question, so her i just say something i know. the role of pressure in incompressible flows is a lagrangian multiplier, which means the pressure demands the velocity field you obtained (with the moving the pressure to the right-hand-side of momentum equations) satify the conservation of mass. with pressure on the right hand side, where the pressure can be obtained by the approximation from the previous time step, you can get a velocity field. but you can a lot of, as a matter of fact infinite number of, velocity fields. however, such a field must satisfy the continuity equation. in penalty formulation, you can incorporate the continuity equation into the momentum equation & kind of limintate the pressure. so, you can work out the velocity field alone. penalty formulation reflects the epcicenter of "lagrangian multiplier" literatelly, but it is a bad approach and i surely suggest you not go for it. in compressible flows, the navier-stokes flows are solved in a mixed formulation, which simply means the most natural approach. unfornulately, at low sonic speed, the stiffness issue occurs and the mixed approaches does very poorly. you may use artificail compressibility or pressure stabilization methods, to try to extend the "mixed formulation"-which is excellent for compressibel flows & compressible elasticity to the incompressible limit. unfortunately, the extension is not successful, either due to implemental complexibity or performance/speed or both. so, the best category of handling incompressible flows is the splitting. and there are 3 categories for this business: 1. continuous splitting: you can derive a pressure poisson equation from the momentum and continuity, in a continuous sense; and impose boundary a neumann boundary condition for the pressure poisson; the boundary condition can be derived from application of momentum equation on the normal direction of the boundary. this approach is a little pain at the beginning, due to the boundary condtion; but once you have then ready, it's easy to proceed; 2. discrete splitting: you can continue the "mixed formulation" or the natural formulation, and get all matrices; then you do some manipulations to get a sub systems for the velocity and a pressure-poisson-like subsystem for the pressure. this apporach share a lot with the mixed formulation, so that it's easy to communicate with traditional compressible slovers. unfortunately, you still need add additonal boundary conditions onto matrices you just got. the reason, after you convert the matrices you just got into subsytems for the velocity and pressure, some information may get inactive, even the conversion is a one-on-one conversion. there are other types of discrete splitting, such as the one presented in the famous paper published in 1965 on "physics of fluids", in which this technqiue, finite volume method, staggered grid, and MAC free-surface capturing technique can be found (in one single paper -- can we find this kind of highly original papers now?) 3. semi-discrete approach this is simply the famous "fractional step" or "projection" by Chorin. I don't the "velocity correction" approach implemented in "Fluent" belongs to which category, such as SIMPLE, SIMPLER, and so on. but the procedures being used by commercial software must be good, which is not necessary a case for those published on journa papers. |
Re: Pressure enigma.
a little calrification:
suppose we onvert system A to system B, in a one-on-one manner. we might think: since these two systems are equivalent to each other, solving B is the same as soliving A. unfortunately, this is a wrong idea. system B indeed equates system A, they contain the same information; however, some information may hide inside the system and simply can't be utilized. in other words, some information stored in system A may become intrinsic in B. as a consequence, we can't solve B and get the correct results. |
Re: Pressure enigma.
"pressure is just the pressure, the normal-direction force per area acting on the surfaces you are interested in. nothing fancy for the pressure in incompressible flows, in terms of concept. "
I'm a bit confused here, let me reformulate my first question: Do we have some pressure acting in the incompressible system other than the dynamic pressure? |
Re: Pressure enigma.
You have the static pressure, but in terms of the solution of the equations all that is important is the pressure gradient. You can add or subtract a gauge pressure from the flo field and get the same velocity field.
|
Re: Pressure enigma.
Is it possible to eliminate the pressure term (by say assuming p = 0.5*rho*uČ) and do a least-squares fit to the resulting two equations (x-momentum and continuity) in a 1d problem?
|
Re: Pressure enigma.
Yes. So what is the pressure gradient in an incompressible fluid? I understand that it resolves from the solution of the equations but is there a physical meaning behind it?
|
Re: Pressure enigma.
In the incompressible equations the pressure (usually referred to as the dynamic pressure to distinguish it from the thermodynamic one) is the internal force required maintain mass conservation (which also prevents cavitation). Basically it describes the coupling between the momentum equation and the continuity equation;i.e. it's the force required to ensure that the velocity evolves in a manner that conserves mass (strictly speaking it's volume in the incompressible equations). If you know about classical mechanics (Lagrange & Hamilton) then in an inviscid fluid the pressure (p) is the "Lagrange multiply" that multiplies the mass-conservation constraint when added to the Lagrangian -variations with respect to p gives the mass conservation equation while variation of the other parameters yields the momentum equations.
|
Re: Pressure enigma.
The interpretation of the pressure in incompressible flow as a Lagrange multiplier is the result of a particular mathematical analysis of NSE. If the equations are rewritten in the stream function-vorticity form or the stream function form, there is no pressure in the problem. The incompressible velocity field exists and can be computed without regard to the pressure. The incompressibility/mass conservation is being maintained without reference to a pressure. Where is a Lagrange multiplier in this case? If one expands the velocity field in terms of a divergence-free basis, the expansion will always be divergence-free no matter what expansion coefficients are chosen. If the expansion coefficients are chosen to best approximate the solution to the NSE, this solution will be divergence-free without regard to the pressure. The incompressibility condition acts like a conservation law. The "pressure" derived from the velocity field (say by the pressure Poisson equation) is that pressure-like quantity consistent with the flow field. How can we say that the pressure drives incompressible flow if there is no pressure appearing in the governing equation? Incompressibility drives the flow and pressure responds!
|
Re: Pressure enigma.
"The interpretation of the pressure in incompressible flow as a Lagrange multiplier is the result of a particular mathematical analysis of NSE."
No - it follows from the derivation of the inviscid equations using a Lagrangian. This is also true for compressible flows! The streamfunction is the mathematical device. It's just a way of hiding the pressure, just like using the vorticity form in the 3D problem. "The incompressibility condition acts like a conservation law." No - it behaves as a constraint on the flow. The pressure is gradient is the force required to enforce the constraint. The constraint actually corresponds to the conservation of volume not mass (unless density is constant). Sara, If you're OK with the (thermodynamics) pressure in the compressible equations then one way of understanding the corresponding term in the incompressible equations is to nondimensionalize the compressible equations and perform a low Mach number asymptotic expansion of the equations. There are many examples of this procedure in papers within the Journal of Fluid mechanics. |
Re: Pressure enigma.
Excellent answer Jonas, thank you, this was the essence of my confusion.
|
Re: Pressure enigma.
No No No The confusion,if there is any, is the result of the definition of pressure in the mechanical sense, i.e., the normal component of force ..etc. The Kinetic theory of Gases gives the definition of pressure as the momentum exchange between the molecules or between the molecules and solid boundaries. in other words, it is another thermodynamic property of matter. If you adopt this definition then there will be a pressure whether we treat the flow as incompressible or compressible or whatever. It is a property of matter. Good Luck.
|
Re: Pressure enigma.
But the original question was about INCOMPRESSIBLE flow.
|
Re: Pressure enigma.
i suggest you not to try these kinds of approaches.
in fundamenatal and long-standing things, it's better to use something popular; once you reach to the front of the research field, try hard something unconventional |
The original question was about the PHYSICAL interpretation of pressure, so forget Lagrange multipliers.
Suppose you have a fluid completely at rest. The molecules are moving at high speed with random thermal motion. The molecules collide either with a real surface, or with the molecules on the other side of an imaginary surface. The average of these forces of collision give a normal force (the tangential forces cancel statistically) called the pressure. Now, if there is a velocity gradient the tangential forces do not quite cancel and a normal and a shear force are exerted on the surface. The normal force is called pressure and the tangential force is called viscosity. Incompressible or compressible - same thing |
Quote:
Interesting discussion. So where does this put compressible flows, seeing that we use the thermodynamic pressure in the cNSE, which magnitude depends on effects we do not model? Is it one part "physical reasoning" and one part numerical? |
Quote:
This is a very old discussion that dates back to the 19th centuray and when the Navier Stokes equation was written. But it would be of benfit if we recall the origin of the incompressible flow definition, so here it is, Engineers have found that in a process where changes in the density of a fluid are less than 3% can be neglected and hence we can treat the flow as a constant density fluid/flow. The result of this engineering criterion is that the divergence is Zero and hence the simplified Navier Stokes equation. In short, when that criterion is adopted, we say that density changes are neglected and nothing more than that. (bear in mind that density changes may be the result of pressure or temperature changes or both) but for engineering design purposes we neglect that change in the magnitude of the density but not in the causes of that change. Hope that will help |
If we consider the continuity and momentum equations for a general compressible fluid:
![\frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0 \frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0](/Forums/vbLatex/img/1194ad2165bd70d6ccac3f24ea514126-1.gif) ![\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0 \frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0](/Forums/vbLatex/img/5d8b30cb9598ed5bda495dcb5ce01e1d-1.gif) taking the time derivative of the first one and the divergence of the second one: ![\frac{\partial^2 \rho}{\partial t^2} +
\frac{\partial}{\partial x_j}\left[\frac{\partial \left( \rho u_j \right)}{\partial t} \right] = 0 \frac{\partial^2 \rho}{\partial t^2} +
\frac{\partial}{\partial x_j}\left[\frac{\partial \left( \rho u_j \right)}{\partial t} \right] = 0](/Forums/vbLatex/img/6f2f3727f31ff6e507173603e8a990f6-1.gif) ![\frac{\partial}{\partial t}\left[\frac{\partial \left( \rho u_i \right)}{\partial x_i} \right] = -
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] \frac{\partial}{\partial t}\left[\frac{\partial \left( \rho u_i \right)}{\partial x_i} \right] = -
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right]](/Forums/vbLatex/img/ab52f861fac8af8cf958682457e653ce-1.gif) and finally substituting the second in the first one, we get: ![\frac{\partial^2 \rho}{\partial t^2} =
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] \frac{\partial^2 \rho}{\partial t^2} =
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right]](/Forums/vbLatex/img/5fa795eb9d663dd3950c0b7a5ce1f803-1.gif) with: 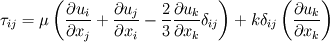 Now, considering single component flows, we have: 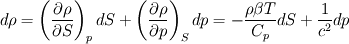 Obviously, as also stated by someone else, an incompressible fluid doesn't even exists. For the present task we can assume the FLOW (not the fluid) as isothermal and we'll get (which, however, is the same of getting 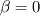 ): ):![\frac{1}{c^2} \frac{\partial^2 p}{\partial t^2} =
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] \frac{1}{c^2} \frac{\partial^2 p}{\partial t^2} =
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right]](/Forums/vbLatex/img/af887cf59bc2f99ce4f4c9b32f442a50-1.gif) And finally moving all the pressure terms to the left side: 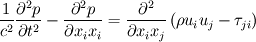 Considering the last equation (which, i think, should be correct) we can say something about the nature of the pressure. In fact, mathematically speaking, it is similar (somehow and neglecting some lower order terms) to an externally forced mass-spring system with 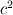 playing the role of k, the elastic costant of the spring. playing the role of k, the elastic costant of the spring.So, what happens when k is very high? In the mass spring-system, after some very fast oscillations (the more k is high the more they are faster), the mass will assume a displacement in equilibrium with the external forcing. The same is true even if the external forcing is not costant but relatively slow, and at every time the mass can be considered in equilibrium with the external force. In this case the problem is called stiff because the time scale of the system is very different from that of the external forcing. Going back to the pressure equation, the role of k is now played by 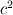 , the speed of sound in the fluid. When , the speed of sound in the fluid. When 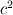 is very high but the fluid velocity is relatively slow compared to is very high but the fluid velocity is relatively slow compared to  , the problem becomes stiff, that is the thermodynamic is much more faster than the external forcing; this comes out nondimensionalising the right hand terms with , the problem becomes stiff, that is the thermodynamic is much more faster than the external forcing; this comes out nondimensionalising the right hand terms with 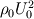 . .Actually, in this case, the thermodynamic nature of the pressure is not changed (why should it be?) but (first of all for computational purposes) we can consider a new equation in which the time derivative term is omitted because of the 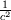 term (being of lower order): term (being of lower order):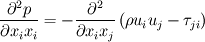 Moreover, with a very lenghty procedure, it can be shown that the divergence of the velocity field is proportional to terms involving 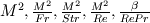 , so, in the same hypothesis already made, it also is of lower order and can be assumed to be zero, so we finally get: , so, in the same hypothesis already made, it also is of lower order and can be assumed to be zero, so we finally get: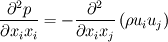 Which is of very different nature respect to the original one, being an equilibrium equation for the pressure (not a time-evolution one), so at every time the pressure is considered in equilibrium or, mathematically speaking, the pressure is considered acting as a Lagrange multiplier for the velocity field; in fact the equation is now a cinematic condition on the velocity field which has to be fulllfilled at every time. So, what actually changes between the incompressible view and a general one, it's not the pressure nature, which is still thermodynamic, but the parameters affecting it. Actually, in the incompressible view, we are considering the pressure as affected by normal momentum fluxes only and, because the pressure fastly recovers the equilibrium after a momentum change (because of the 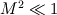 hypothesis), we just consider it as in equilibrium at each time omitting the lower order time-derivative term. As i said, this is much more a computational necessity (because of the stiffness); in fact, if you are interested in acoustic you will need to retain the time-derivative term and use one of the method of the computational aeroacoustic to treat the equation. hypothesis), we just consider it as in equilibrium at each time omitting the lower order time-derivative term. As i said, this is much more a computational necessity (because of the stiffness); in fact, if you are interested in acoustic you will need to retain the time-derivative term and use one of the method of the computational aeroacoustic to treat the equation.Sorry for the lenghty post but i hope it helps. |
Quote:
|
I would like to continue this discussion by asking the following question:
If we have an incompressible fluid in a near vacuum domain then what happens if the "motion driving pressure" differences are large enough to cause the absolute pressure to be negative in some parts of the domain? Can we really relate the motion driving pressure to the thermodynamic pressure? |
| All times are GMT -4. The time now is 12:41. |