 |
|
|
[Sponsors] | |||||
Diffusion Equations coupled by Boundary Conditions |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Michael
Join Date: Mar 2016
Posts: 4
Rep Power: 10  |
Hi, I'm new here and not sure whether my question is in the right place.
I have the following problem: I'd like to solve two diffusion equations, e.g. 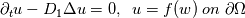 and 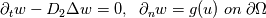 which means the PDEs are coupled by their boundary conditions. The solution of u depends on w by a Dirichlet BC. And w depends on u by a Neumann BC. At the moment I first solve the equation for u, then compute g(u) and afterwards solve the equation for w, which allows me to compute f(w) for the next iteration, etc. .... This works very nice for the stationary case, i.e. for 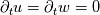 For the time dependent case however....the method is highly unstable. I'm searching now for a method to solve both equations simultaneously, somehow - instead of one after another. But I have no clue how to do this. If one searches for literature about this issue, it seems nobody has ever had the problem to solve PDEs coupled by boundary conditions. Any hint? Any literature? Ideas? BTW: I'm not working with any commercial software, but a own FEM software written in Fortran. Therefore please don't recommend commercial software. Greetings, Amiga-Freak |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Quote:
numerical instability appears if you do not use a time step within the stability region. What criterion have you used? |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Michael
Join Date: Mar 2016
Posts: 4
Rep Power: 10  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
What about the functions for the bc.s ?
|
|
|
|

|
|
|
|
|
#5 |
|
New Member
Michael
Join Date: Mar 2016
Posts: 4
Rep Power: 10  |
||
|
|

|
|
|
|
|
#6 |
|
New Member
Join Date: Apr 2014
Posts: 11
Rep Power: 11  |
It seems that your instability (I am saying this without knowing anything about the way you implement this numerically...) is due to the fact that while the equation system is elliptical (everything happens instantaneously everywhere at each time-step), you introduce a time-lag between the first equation and the second.
Did you write the solver yourself? In that case, writing it to solve the two equations at the same time should be straight-forward. A more elegant solution would be to write the solver as implicit. Compared to Navier-Stokes equation, your set is relatively simple and, above all, linear. This means that the implicit solver, even in 2D and 3D, remains quite simple. The advantage is that the boundary conditions are imposed at the same of the solution. If you did not write the code, you may "trick" the solver into solving both equations (they are the same) by using a vector that is twice as big {u | w} instead of each vector {u} and {w} |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
The set of equations is parabolic in the unsteady case and classical numerical integrations, such as the Crank-Nicolson method, can be used.
The only care is to provide BC.s that ensure that the time derivatives do not blow-up. For example, the Neumann BC.s for w can be critical, it is simple to see that by integration over the whole computational domain V: d/dt Int [V] w dV = D2 Int[S] g(u) dS Therefore, if g(u) is such that Int[S] g(u) dS > 0 then the integral of the w will blow-up in time |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Join Date: Apr 2014
Posts: 11
Rep Power: 11  |
Thanks for the correction, FMDenaro. I guess I overlooked the derivative over time.
I agree, parabolic --> Crank-Nicholson Please, disregard my previous comment |
|
|
|

|
|
|
|
|
#9 | |
|
New Member
Michael
Join Date: Mar 2016
Posts: 4
Rep Power: 10  |
No, I'm a PhD student and the solver was written by other PhD students before me, several years ago.
Quote:
Maybe It's easy and I'm just dumb, but I don't see how to do this. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| sliding mesh problem in CFX | Saima | CFX | 46 | September 11, 2021 07:38 |
| Radiation in semi-transparent media with surface-to-surface model? | mpeppels | CFX | 11 | August 22, 2019 07:30 |
| GETVAR Error in Multiband Monte Carlo Radiation Simulation with Directional Source | silvan | CFX | 3 | June 16, 2014 09:49 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 06:20 |
| Radiation interface | hinca | CFX | 15 | January 26, 2014 17:11 |