 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Guest
Posts: n/a
|
Hi, John I didn't read your answer to manjgi question. Actually I said one more time what you have already said, while using not as many words as you did. One small addition: the best way to lower your Reynolds number is to increase your density. You might use very very very high densities. In this case your code MUST work. If not try to find the bug.
best regards Jannis |
|

|
||
|
|
|
#22 |
|
Senior Member
Join Date: Mar 2009
Posts: 138
Rep Power: 17  |
Hello Everybody!
I am also struggling with convergence problems, so I found this thread. Now I have some question to Y+ (1) As I was told 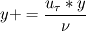 and and 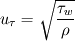 (by the way: what is y?) (by the way: what is y?)So y+ is part of the solution and not a attribute of my mesh? According to that y+ is also conditioned by my boundary conditions? (2) Which Size should y+ have? I was told y+ <1. In this thread it is suggested 50<y+<300 and here: http://www.cfd-online.com/Forums/openfoam-solving/59331-y-cell-aspect-ratio.html they say it should be smaller than 5 (3) I have a computation perfektly converged but yPlusRAS gives me an average of about 1600 for y+. Does this mean the solution is incorrect? (4) I am using simpleFoam with k-Epsilon Turbulence Model. Do I have to care about y+? Because in my Opinion k-Epsilon is using a wall function. Mmm a lot of Questions! I am thankfull for every hint! Saludos |
|
|
|

|
|
|
|
|
#23 |
|
Senior Member
Ahmed
Join Date: Mar 2009
Location: NY
Posts: 251
Rep Power: 18  |
Yes, a lot of analysis faces convergence problems, the way to solve this kind of situations is straight forward. Convergence is a mathematical concept, and if you carefully look at any analysis technique (in the context of CFD) and if it is a Finite Element, Finite difference or Finite Volume, there is one common base line, all these techniques lead to the formation of a matrix that has to be solved.
Ask yourself What causes a matrix to be solved or not and what can be done to ease the difficulties then you have the answer to your original question. Yes, the aspect ratio as mentioned in a previous post, is a very important factor (think in terms of the matrix you are solving). Cheers and good luck.   
|
|
|
|

|
|
|
|
|
#24 | |||
|
Member
Jed Brown
Join Date: Mar 2009
Posts: 56
Rep Power: 19  |
Quote:
Quote:
Quote:
|
||||
|
|

|
||||
|
|
|
#25 |
|
Senior Member
Ahmed
Join Date: Mar 2009
Location: NY
Posts: 251
Rep Power: 18  |
Jed
I patiently googled for the paper till I located a ps file that I downloaded and read. what can I say? too much mathematics. In solving a matrix, simple arithmetic operations of division, multiplication and subtraction are involved and if these operations fail, the solution is difficult to arrive at. let us see:- 1- Well posed physical problems never lead to singular matrices. 2- near singular matrices are difficult to solve so what applied scientists can do in order to avoid near singular matrices? The only tool we have is the mesh quality. Boundary conditions are imposed by the physics they represent Or to say it in other words, can a mesh with aspect ratio of 2 or higher lead to a matrix that converge at the same rate as a matrix representing a mesh whose aspect ratio is 1.1 or 1.2 I am not trying to over simplify the problem, just I want to use a language that is understood by every one involved in a serious real world cfd analysis. Cheers and good luck to all   
|
|
|
|

|
|
|
|
|
#26 | |
|
Senior Member
Ahmed
Join Date: Mar 2009
Location: NY
Posts: 251
Rep Power: 18  |
Quote:
|
||
|
|

|
||
|
|
|
#27 | |
|
Member
MrFluent
Join Date: Mar 2009
Posts: 33
Rep Power: 17  |
Quote:
For wall cells the velocities are known thus you know the convection terms. Usually flux is zero. So convection terms are zero. Now for the diffusional terms you have no idea how to get them. So a simple way is to assume a linear profile and find out shear stress by formula tw = visc * (du/dy). For this you know viscosity and du/dy can be obtained by velocity profile. However the main issue is that if profile is not linear where you cell center is the above formula gives wrong shear stress. So log wall law is proposed. And used for calculating shear stress. If k and omega are used in calculating y+ u+ etc, wrong values of k omega could cause diveregence. So very fine mesh and with no wall model may be more stable. |
||
|
|

|
||
|
|
|
#28 |
|
Member
Jed Brown
Join Date: Mar 2009
Posts: 56
Rep Power: 19  |
You seem to have completely missed my point. Globalization is hard due to nonlinearity. If you have a problem solving a linear system, it almost always means that you have blown the preconditioner. Sometimes a direct solve is the only thing that works reliably, and even they fail in rare cases, but this normally triggers an error. Most causes of a nonlinear solver failing to converge will not be fixed even if the Jacobian is solved exactly.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| convergence problem when use pisoFoam, LES for wind tunnel case | Forrest_Lei | OpenFOAM | 3 | July 19, 2011 06:00 |
| convergence problem | commonyue | Main CFD Forum | 1 | December 1, 2009 03:54 |
| Convergence of CFX field in FSI analysis | nasdak | CFX | 2 | June 29, 2009 01:17 |
| 3D Fluid Flow Convergence problem | Emily | FLUENT | 2 | March 21, 2007 22:18 |
| Non Convergence of 3D Heat transfer cfd problem | Balraj | Main CFD Forum | 3 | December 9, 2004 00:24 |