Hi
Im going through the book 'Computational Fluid Dynamics The Basics With Applications' by John D Anderson and Im trying to do the problems that are at the end of each chapter.
Im currently doing problem 2.2 on page 94 that states:
Derive the momentum and energy equations for a viscous flow in integral form. Show that all three conservation equations-continuity, momentum, and energy-can be put in a single generic form.
Sorry that this is going to be a long post but Im trying to explain how I got my answer so someone cant point out if and where Ive gone wrong.
Ive derived an expression for the momentum equation but there are some terms Im not sure about. I dont have any way to check if my answer is right. And its surprisingly difficult to find the momentum equation in integral form in literature and on the web.
I applied the principle of conservation of momentum to a finite control volume that is fixed in space with the fluid moving through it.
The physical principle is that the forces acting on the body of the control volume are equal to the rate of change of momentum. I concentrated on the forces first.
I split the forces into body and surface forces.
I also defined a term
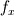
that denotes the body force per unit mass.
Hence the term for the body forces acting on the C.V. is given below:
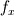

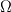
means volume.
Now I found an expression for the surface forces. I used a small surface element on the surface of the control volume. This has a force arrow pointing out the midpoint of the elemental surface and a normal vector that is perpendicular to the surface.
Using the stress tensor we can find the normal and shear stresses on the surface of the element. The stress tensor is defined below:
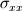
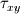
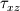
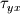
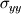
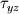
=
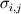

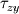
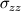
The dot product of the stress tensor with the normal vector gives you the magnitude of the force on the surface element in the direction that it acts in (which is not the surface normal). Summation over the entire control surface of the elements gives you the expression below:
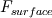
=
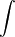
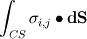
Where
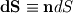
Then I went on to the expressions defining rate of change of momentum.
This involves two terms. One for the rate of change of momentum of the control volume and another for the rate of change of momentum of fluid entering and leaving the CV.
The first term started with first defining the momentum of a small cube element of the CV then summation of that element to find the momentum of the entire CV to which we can apply a rate of change. This lead to teh following expression:
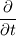
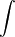
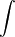
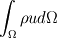
The second momentum term came from considering the mas flow rate coming in and out of the CV and multiplying this by velocity to give the rate of change of momentum. We get the total rate of change of momentum going in and out of the CV once we sum over the entire surface. The expression I arrived at is given below:
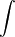
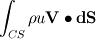
Bringing all the terms together we get:
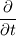
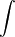
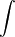
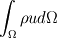
+
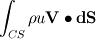
=
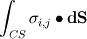
+
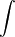
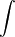
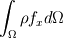
Im not sure how correct I am with this expression thats why Im here asking for some help in having it checked over. The momentum equation is a vector equation that has three directions x,y, and z which is the way it is expressed in its differential form. From the above expression this seems to be the case for the integral form too. The changes in the y and z expressions would be the u velocity used in the first two terms and the fx body force per unit mass value in the last term.
This is my dilemna though, if the equation only deals with momentum in the x-wise direction then I have terms in the equation that deal with forces and momentum in all directions. Such as the stress tensor term. The stress tensor takes into account all the stresses in all the directions which I should be not be using? The term above would then give me a summation of all the forces in all directions and not just the x-wise normal and shear stresses. Do I need to use a stress tensor that only contains values for the stresses in x-wise direction only?? Such as
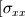
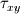
![\tau_{xz} ] \tau_{xz} ]](/Forums/vbLatex/img/3d0b7c8a33513cbf64252343c3237b2e-1.gif)
.
I have the same problem with the second term where the velocity vector
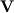
is used. Surely this gives the rate of change of momentum in all directions and not just the x-wise direction. But the use of u in that term then makes me think it might only be x-wise momentum.
If my equation is correct please help explain to me why those two terms only refer to x-wise momentum and forces. And if im wrong then please correct me and explain where I went wrong. Thanks in advance for any help.

