
 |
SIMPLE algorithm
Hi,
I have written the SIMPLE algorithm in Matlab (using an example 6.2 from Versteeg and Malalasekera: An Introduction to Computational Fluid Dynamics: The Finite Volume Method) for 1D, steady, incompressible, frictionless flow using a backward staggered grid and an upwind differencing scheme through a nozzle. The example uses 5 pressure nodes, and I get my program to converge to the Bernoulli solution (albeit quite inaccurately due to the coarse mesh). When I changed the program to handle N nodes, I had problems with convergence for any more than 5 nodes. The example in Versteeg applies both velocity and pressure under-relaxation factors (urf) at the end of the algorithm before substituting the new u and p field back into the discretised momentum equations: u = (1-urf).u_new + (urf).u_old p = (1-urf).p_new + (urf).p_old which for the 5 node case suggests using urf as 0.8. I later found that for 5 nodes I can use urf=1 and the solution still converges. Then, having looked at Patankar (Numerical Heat Transfer and Fluid Flow), I scrapped the pressure urf from this bit of the algorithm and moved it to: p=p*+p' =>to become=> p = p* + urf.p' However by doing this I found that urf is very sensitive to the number of nodes that I wish to use. I built in a loop to find the optimal urf by reducing the urf (from 1) by 0.01 each time the program started to diverge, and I did this for up to 100 nodes. This told me that I do not need to apply an under-relaxation to velocity (so I kept it at 1), only to pressure (urf_p). To give an example of a few... 5 nodes: urf_p = 1 10 nodes: urf_p = 0.49 20 nodes: urf_p = 0.20 25 nodes: urf_p = 0.15 40 nodes: urf_p = 0.08 50 nodes: urf_p = 0.06 75 nodes: urf_p = 0.04 80 nodes: urf_p = 0.04 100 nodes: urf_p = 0.03 Applying this and I can get convergence for up to 100 nodes, with the velocity and pressure fields becoming ever more accurate (with Bernoulli). However to increase the number of nodes further, I have to drop the urf_p down even further. The optimal urf_p seems to be proportional to a 1/N relationship (N=number of nodes). So if I want an even more accurate solution, say for 10,000 nodes, I have to use urf_p=0.0002 in order to get convergence, where I get an error in the mass flow rate on the order of 0.01%. Speed it not really a problem at the moment, even for 10,000 nodes I can get a converged solution in around 10 minutes. Basically the question is to whether this sort of behaviour is normal? |
This behavior IS to be expected from the SIMPLE algorithm. I'm working on my masters in thermo/fluids and am also writing code for control volume methods. The slow rate of convergence and poor prediction of pressure fields are due to dropping the velocity contributions from neighboring nodes and using only the pressure field for corrections.
Patankar addressed this issue through the SIMPLER alg. (SIMPLE Revised). SIMPLER requires additional computation steps, but achieves the correct velocity and pressure fields in the same time as SIMPLE. I got this information from a book written by Majumdar called Computational Methods for Heat and Mass Transfer. It describes several of these algorithms in detail including an example. I hope this has been helpful. -Best Regards |
Thanks for getting back to me, Scott.
Unfortunately my college library does not have the book you mentioned, so I've been looking at SIMPLER in both Versteeg and Patankar. For the SIMPLER algorithm, in the calculation of the pseudo-velocities, am I right to assume that momentum source term 'b' is zero in case of 2D convection-diffusion?? In that case I would be left with: uPSEUDO = (aW.uW* + aE.uE* + aN.uN* + aS.uS*)/aP where aP = aW + aE + aS + aN + (Fe-Fw) + (Fn-Fs) Therefore in the calculation of the pseudo velocity, you do not need to a pressure field. Again, am I right in saying this? Thanks |
please help me
hi i am trying to write the code SIMPLE in the c language by using the upwind scheme but i am not getting how to start the code
so please send me theSIMPLE code Quote:
|
Colocated grid - boundary condition
Hi Scott,
I have written a solver (FVM) with staggered grid arrangement and it is working well (compared with fluent solver also). But it is not robust for different geometries. So i started working on the colocated grid. I have taken a simple 1d grid (assuming a diffuser or a nozzle) with varying area at different nodes. I am writing a cell centered FVM. I have tried with different conditions (bc's). Solution is diverging for all the condition. I think i have problem in my exit bc. It is as follows: Assuming I have 8 cell centered nodes (or 8 control volumes). 1. Node no.1 is the ghost node. similarly node no.8 is the ghost node. 2. U-Momentum equation is solved for the nodes 2 to 7. 3. At the inlet (CVno.2, basically west face velocity of control volume 2) i am giving the velocity inlet bc. 4. Pressure at the ghost node 1 is taken from node 2 (i.e p(1)=p(2)) 5. Similarly for velocity u(1)=u(2) (these velocities are nodal and not face) 6. At the exit i am extrapolating nodal velocity like u(8)=u(7) and the face velocity equal to u(7) (i.e ue(7)=u(7) where ue(7) is the east face velocity of node 7) 7. My pressure at the exit is p(8)=0 Please tell me Whatever i said above is right or do i need any in my boundary condition. Please help me in this regard thanks Jyothish |
Hello,
please send your source code SIMPLE / SIMPLER scheme through my email, ahazbavi@ymail.com. |
hi i have written a code that used simple code in fortran.
it is ac ode for flow in a tube that there are two rectangular obstacle inside. i can debug your code if i see it....send it to me if you like. morteza08@gmail.com |
SIMPLE algorithm code
Hi everyone;
I have worked on phase change materials and I have done some simulations on Fluent. At this time I need to use SIMPLE algorithm code in order to get velocity- pressure coupling. However, I have difficulty in coding SIMPLE algorithm as tool. So, if anyone has worked on SIMPLE algorithm, I really appreciated send it to me on my e-mail, azeldin.elsawi@gmail.com |
Fluent for Phase change materials
Hi everybody;
I would like to know the viscosity could be changed in Fluent as case of phase change materials. |
simple
hi
i need that coding, could u please send me, it should be very useful for me. i just try in the fortran. thanks........................ |
Example 6.2 matlab file
Can somebody send me the matlab file for this please. I really need it. I will really appreciate it.
|
please send me this code
Could you please send me this code at banmakadachha@gmail.com
|
|
request
can you please send the code at dasguptadebayan@gmail.com
|
Request
please, can you send the code at eng.aliazzam89@gmail.com
|
Hi, @SamR
Same question is my homework, could you please send me this code ? Thank you so much ezgiiypc@gmail.com |
Hi, @SamR
my homework in CFD Course is same, could you please send me this matlab code ? Thank you so much bambangwahono80@yahoo.co.id |
Quote:
Im writting the same problem in fortran 90; I got the same (under-relaxed) results until the first iteration for 5 nodes, it means: u1=1.78856 u2=2.29959 u3=3.21942 u4=5.36571 and also I got: pA=9.08536 pB=8.8115 pC=8.3396 pD=7.4664 pE=0 the issue is that once I run the next iteration, I dont get the mentioned equation in the book, at node 1: 1.20425(U1)=1.98592, I get: 1.14848(U1)=1.412218 I did it by hand, I dont know what I am doing wrong. |
Need help
Hi, It's nice to meet you here. I am a Ph.D research scholar, working on EVAPORATION OF LIQUID DROPLET. I have developed a model using the stream function-vorticity method where the differential equations are discretized using the Power Law method as per Patankar book. However, I am facing little bit difficulties in handling source term as it has COT(
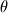 ) term. ) term.Do you have a CFD code/model on Spherical Coordinate for SIMPLE/SIMPLER algorithm which is written in FORTRAN programming language for solving complete Navier Stokes Equation? I have a basis CFD code written by Patankar which can handle only 2D cartesian and polar coordinates. if anyone needs this code, kindly give me a mail. I need help in discretizing Navier Strokes equation for Spherical Coordinate by Power Law method as per the Patankar book. Thanks. Numan Siddique Mazumder email: siddiquesil@gmail.com |
If anyone is interested in comparison or needs an implementation example, check out my implementation of the Versteeg example 6.2 on my github page! I implemented SIMPLE and SIMPLER with an algebraic multigrid linear solver library AMGCL, as well as basic Gauss-Seidel iteration. I have not conducted a spatial convergence study but it does get very close to the exact solution with 10000 nodes. With AMGCL enabled, the speedup is incredible. It currently uses the Biconjugate gradients stabilized method, but can be changed to a few different methods supported by the library.
|
| All times are GMT -4. The time now is 05:57. |