 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
kmlin
Join Date: Mar 2010
Posts: 2
Rep Power: 0  |
Hi everyone,
As title, my question is how to implement the TVD scheme (Flux/Slope limiters) implicitly. For example, If we define F(n+1, j+1) as the function at n+1 time step and j+1 cell, we can represent the general one-parameter family of explicit and implicit schemes of the following form u(n+1, j) + lamda*theda*[ h(n+1,j+1/2) - h(n+1,j-1/2)] = u(n,j) - lamda(1-theda)[ h(n,j+1/2) - h(n,j-1/2) ] where "lamda" is a constant, "theda" is used to control the scheme is explicit or implicit, and "h" is the flux function containing limiter such as MINMOD. My question is how to implement the MINMOD in h(n+1, j+1/2) in the implicit scheme. Should I just use the information of previous time step and evaluate it explicitly? Thanks. |
|
|
|

|
|
|
|
|
#2 |
|
Member
Jed Brown
Join Date: Mar 2009
Posts: 56
Rep Power: 19  |
For a one dimensional scheme, it could be useful to assemble the matrix based on differentiating through the limiter, but in 2D and especially 3D, this will produce a Jacobian that's just too expensive to work with. Actually computing the stencil is somewhat messy to do by hand, so you may want to consider automatic or symbolic differentiation. I would recommend using a Jacobian-free method preconditioned by a first-order operator. Use of differentiable limiters is useful in this context. A good paper on this:
Code:
@article{gropp2000globalized,
title={{Globalized Newton-Krylov-Schwarz algorithms and software for parallel implicit CFD}},
author={Gropp, W. and Keyes, D. and Mcinnes, L.C. and Tidriri, MD},
journal={International Journal of High Performance Computing Applications},
volume={14},
number={2},
pages={102},
year={2000}
}
|
|
|
|

|
|
|
|
|
#3 | |
|
New Member
kmlin
Join Date: Mar 2010
Posts: 2
Rep Power: 0  |
Quote:
If possible, would you please show a little bit more explicit on the formulation of MINMOD (or some other limiters)? I have totally no idea how to formulate a function with "max(0, min(1,r)" or (r+|r|) / (1+|r|) which is the flux limiter? I have found dozens of papers talking about limiters, but none of which shows how to do this formulation. Or where I can find some useful materials on this? Thanks Kmlin |
||
|
|

|
||
|
|
|
#4 | |
|
Member
Jed Brown
Join Date: Mar 2009
Posts: 56
Rep Power: 19  |
Quote:
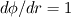 if if 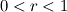 else else 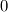 . Newton methods don't work great because the derivative is discontinuous, which is why you should probably use a . Newton methods don't work great because the derivative is discontinuous, which is why you should probably use a 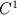 limiter for implicit methods. Of course you have to differentiate again to get the derivative with respect to the jumps, and again to get a derivative with respect to the stencil (which is what you need to assemble a matrix). I recommend using automatic differentiation for this, it's not worth your time to work it out by hand for 20 different limiters. And I still recommend using a Jacobian-free method, in which case you don't have to do this differentiation at all, and you can precondition with a first-order scheme which is cheap to assemble. limiter for implicit methods. Of course you have to differentiate again to get the derivative with respect to the jumps, and again to get a derivative with respect to the stencil (which is what you need to assemble a matrix). I recommend using automatic differentiation for this, it's not worth your time to work it out by hand for 20 different limiters. And I still recommend using a Jacobian-free method, in which case you don't have to do this differentiation at all, and you can precondition with a first-order scheme which is cheap to assemble.
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| how to implement MINMOD limiter ? | alan | Main CFD Forum | 0 | November 25, 2008 10:57 |
| Limiter function in TVD schemes | marym | OpenFOAM Running, Solving & CFD | 2 | August 28, 2008 15:59 |
| TVD limiter question | shuo | Main CFD Forum | 0 | February 29, 2008 21:32 |
| why tvd limiter can lead to oscillation | migao | Main CFD Forum | 5 | June 6, 2007 17:53 |
| TVD | student | Main CFD Forum | 6 | September 9, 2002 09:19 |