
 |
hi,
"Up" does not necessarily equal to "U" in position of "P". it deoends the upper and lower bounds of your integration. for example if you integrate the momentum equation to find discrete momentum equation for "e", your source term will have the form of S=Sc+Se*Ue. and similarly for w, you will find source term to be: S=Sc+Sw*Uw. does it help? |
Thanks for the reply. Actually that's the problem, because the lower and upper bounds of my integration has to be the cell faces, which are e and w. P is the centre point of this cell.
Imagine the control volume is shown as below. w |----------P----------| e I integrate the momentum equation over this control volume. So the unsteady term for example will be of the form 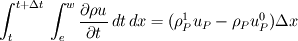 where the subscript 1 is the current time step and 0 is the previous and delta_x is the grid size. Here it is assumed that the grid-point value of u (i.e. the value at P) prevails over the control volume. My problem is, as I mentioned in my first post when I integrate the particular source term that I have, I get 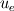 (because the source term is actually in the form of a spatial gradient). If this derivative wasn't there I'd get (because the source term is actually in the form of a spatial gradient). If this derivative wasn't there I'd get 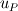 like the unsteady term above. like the unsteady term above.In the original form by Patankar, the full discretised equation will be like 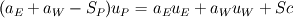 so the Sp term needs to be multiplied by the value of u at the same point (whether it may be e, w or P) as 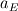 and and 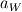 . But I don't know how I could get that. I've seen a number of papers where they've done this for cylinderical coordinates and it should be similar but they never show what the form of Sp they have. . But I don't know how I could get that. I've seen a number of papers where they've done this for cylinderical coordinates and it should be similar but they never show what the form of Sp they have. |
Hi;
you problem seems to be quite fundamental! firstly, you should use staggered contorl when integrating momentum equations. this method is utilized to prevent an unrealistic pressure field. consider the following domain: W----w----P----e----E you should use one of the following CVs for x-momentum discretization: W|-----w-----|P (backward staggered) or P|-----e------|E (forward staggered) the control volume you discussed before is just used for scalar equations discretization such as mass, energy, K, epsilon, etc. Secondly, when you discrete x-momentum equation, convection terms(the right side of momentum equation should not be integrated and probably interpolated just like the way you did. when you have convection term you should use "hybrid", "power-low" or similar methods for stability considerations. after doing this you can organize your source terms. for example if you use forward scheme, all source terms containing "Ue" will be considered as "SeUe" term(just like your SpUp) and the rest (such as "Uw") will be considered as "Sc". (for more information refer to CFD books like the one written by Patankar) dose it help? regards |
Hi,
Thanks for the reply. Firstly even though I drew the control volume as above, I'm actually using a staggered CV for the momentum equations. Secondly I am trying to use the power law for the convection terms, for the Cartesian equations this is straightforward but for spherical equations I have additional geometric source terms that's giving me the problem. The full equation which I'm trying to discretise is 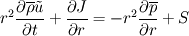 where 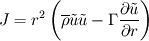 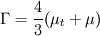 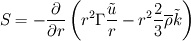 The only problem that I have is the term 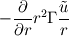 in the source S. This term is a bit like the convective term but I don't know exactly how I would treat it. in the source S. This term is a bit like the convective term but I don't know exactly how I would treat it. I was thinking of putting this in the total convective-diffusive flux term J but then I don't know how to obtain the powerlaw from there. Also this is different to what I've seen in some of the papers. They have the convective-diffusive flux and the source terms as shown above. As I mentioned in my previous post, the problem is when I discretise this source term. Using the forward staggered grid below w---------P|-----e------|E--------e1 I get, 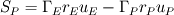 i.e. the velocities here are at the cell faces. However, the discretisation of the convective terms only gives me the velocity 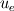 which are the values at the cell centre. So how can I form the source term when this is the case? one of them is at the cell centre and the other at the cell faces? which are the values at the cell centre. So how can I form the source term when this is the case? one of them is at the cell centre and the other at the cell faces?I could use the interpolation of the cell centres to get the cell face values for example 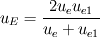 but then I still don't know how I could factorise this interms of 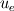 . . |
Hello,
refering to your first post, you can express the Ue, Uw velocities like: Ue=(UP+UE)/2. With this way when you introduce the above equations in the source term, the variable UP appears (together with the UE), which is then inserted in the Sp. Hope it helps a little bit. George |
I realise that I'm going about this the wrong way. I just have to collect the source terms together and multiply it by the volume of the cell.
However, I'm still struggling with the linearization. I've seen a lot of papers and the book by Patankar that explains you how to do this using Taylor series expansion of the source term. For example 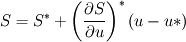 where the superscript * refers to the value at the previous iteration. My problem now is with the differentiation since 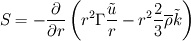 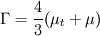 The eddy viscosity 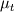 is calculated using is calculated using 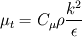 where the variables where the variables 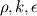 are in general functions of are in general functions of  , this would create a more complex source term with a lot of terms and I'm not sure whether this is the right way to go about this? , this would create a more complex source term with a lot of terms and I'm not sure whether this is the right way to go about this? |
Hi,
on the other hand, you can use a different methodology, where in the source term "Sc" you include all the terms calculated from the previous iteration. This method is not so robust, since it might need some more time in order to converge. Stability issues might also arise. But according to the problem complexity, it can end up to the same calculations. |
Quote:
I have a similar type of source terms in the r-momentum equation which is in derivate form. But as per my last forum post, I was informed that there is no extra source term in the r-momentum equation apart from physical forces which are pressure, centrifugal, Coriolis, gravitation, etc. check the link of my last post https://www.cfd-online.com/Forums/ma...urce-term.html But I have picked up the r-momentum equation from the wiki page which has lots of source terms in it apart from physical forces. The link is here. https://en.wikipedia.org/wiki/Navier–Stokes_equations My questions are as follows. 1. Is the conservative r-momentum equation in spherical co-ordinate given in the wiki page correct? 2. Can you provide me any other link for the conservative N.S equation in spherical co-ordinate? 3. Are there extra terms in momentum equation that arise apart from physical forces for spherical co-ordinate while solving by using FVM? |
| All times are GMT -4. The time now is 23:36. |