Inversion of large sparse linear systems
 

Can anyone tell me some libraries for C languange which inverts large sparse linear systems? It would be better if its install is for linux systems (gcc compiler).

GSL - GNU Scientific Library
Cblas
Clapack

and so on ... any Linux distribution should have the above.

Do

These suggestions are worthless for sparse systems. I recommend PETSc (http://mcs.anl.gov/petsc), it runs everywhere (Linux, Mac, Windows, exotic Unix, and even iPhone ;-)), scales to very large problems (5*10^11 unknowns, ~300k processors), and perhaps most importantly, is easy to extend with custom (physics-specific) solver components, or by composing existing components (including many third-party libraries) at runtime.

OK. Thanks. I have installed PETCs library but i havent concerned it still. Yesterday, i try to use SuperLU library but cant invert matrices (only solve systems). In my problem use the same right large matrix more times. Therefore its not efficient to solve a system at each time. Of course, if i use iterative procedure maybe is ok.

You never want the inverse
 

Maybe you misunderstand the process of "solving". You don't want the inverse because it's dense and numerically unstable. Instead, you factor the matrix, and then solve with sparse triangular factors. This requires far fewer operations than actually creating the inverse, and the triangular solves are also much faster than multiplying by the inverse (roughly 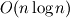in 2D or 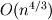in 3D vs. 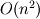, time and space). If you use PETSc, you just call KSPSolve() repeatedly (without updating the matrices), this will reuse the factorization that was computed on the first solve. A standard direct solver would be obtained with (or mumps or umfpack, which are likely faster). Note that larger problems, especially in 3D, may be better suited to iterative methods (domain decomposition or multigrid), even if you need to solve many times.