
 |
Hi Johnhelt,
I'm not an expert on CFD or SIMPLE-like algorithms, but for the past 9 months or so I've been modifying a code written for SIMPLER algorithm and have had to do some discretisations (for a 1-D grid though). I'm assuming that P here refers to the boundary grid point on the bottom surface. Also the 0.5 in your velocity gradient comes from the fact that you're looking at a half-cell. So if you look at the control volume along the z-direction you'd have P----t-----T where t is the face of the CV. So shouldn't the pressure gradient term be 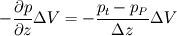 ? ?similarly for the other gradient terms because you integrate between the face of the CV. So for the grid along the x-direction W---w---P---e---E 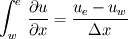 Now if you are looking at the boundary node P at the left-hand-side (LHS) you do not have u_w and u_w can be taken as the value of u_P, which is what you've done when you took w_0 for w_B. |
Hi Lost Identity, and thanks for your fast reply. I think I forgot to mention some nomenclature..
The distance between two nodal points is 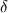 , so then the pressure gradient at P, following your notation, should then be: , so then the pressure gradient at P, following your notation, should then be: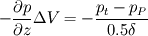 However, the pressure at the 't' face is not known (I'm using collocated variables). You can find it by interpolation 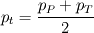 , and therefore you end up with , and therefore you end up with 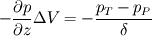 , which is the same as I wrote. So a boost of confidence there :-) , which is the same as I wrote. So a boost of confidence there :-)I'm not sure I get your integration though. At the "bottom" face: B----b----P----t----T after replacing volume integrals with surface ones by the Gauss theorem, the finite volume discretization at the b and t surface gives: 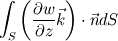 where 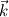 is the z-directional vector and is the z-directional vector and 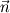 is the surface normal vector. Carrying out the dot product and integrating you get: is the surface normal vector. Carrying out the dot product and integrating you get: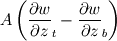 so I need to evaluate both gradients at the two surfaces, which can be done by central differences. However, at the bottom surface only 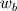 is known is known 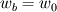 , while the velocity at B is unknown (outside of domain). When using linear interpolation the gradient at b , while the velocity at B is unknown (outside of domain). When using linear interpolation the gradient at b 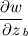 of course ends up being identical to that between b and P. of course ends up being identical to that between b and P.Regards! |
Hi,
Sorry I made a mistake in my integral, missed out the dx and also I was only thinking of 1-D in it. I think that's how I would do it too if I were you. |
Ok a follow-up for those who care...
I'm solving the Navier-Stokes equation for incompressible (laminar) flow to a hole in a plate - and inside that hole as well, where a parabolic flow profile should form. Later I will apply a permeability term to look at the effect of deposition from the flow (filtration). I have implemented the solution using the SIMPLE method with on a structured grid. The whole thing is solved using the preconditioned conjugate gradient method. With regards to the boundary conditions: If I use the approach I wrote in the original post, I get oscillations in the velocity near the inlet in the converged solution. These oscillations, however, die out a few grid points away from the inlet. Instead, I found that specifying the pressure-gradient 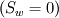 , as well as velocity gradient at the boundary , as well as velocity gradient at the boundary 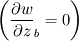 to 0 both, while specifying the velocity at the "bottom" face in the pressure-correction equation to the inlet velocity to 0 both, while specifying the velocity at the "bottom" face in the pressure-correction equation to the inlet velocity 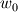 , I get the correct velocity field - without oscillations near the inlet. , I get the correct velocity field - without oscillations near the inlet.I guess it corresponds to specifying the velocity far from the domain, however I could not find any good explanation to this in Versteeg's book.. perhaps someone here can explain? Regards, JH |
| All times are GMT -4. The time now is 20:25. |