 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 15  |
Dear all. I'm currently writing my own FVM code, to be solved by the SIMPLE method. I've run into some issues in defining my boundary conditions that I hope you can help me clarify. Pressure and velocity are collocated.
Say the discretized momentum equation for the w-velocity component in a cubic control volume is (I'm using central difference scheme to evaluate the gradients): ![\mu A \left[ \frac{w_E-w_P}{\delta}- \frac{w_P-w_W}{\delta}+ \frac{w_N-w_P}{\delta}- \frac{w_P-w_S}{\delta}+ \frac{w_T-w_P}{\delta}- \frac{\partial w}{\partial z}_b \right] \mu A \left[ \frac{w_E-w_P}{\delta}- \frac{w_P-w_W}{\delta}+ \frac{w_N-w_P}{\delta}- \frac{w_P-w_S}{\delta}+ \frac{w_T-w_P}{\delta}- \frac{\partial w}{\partial z}_b \right]](/Forums/vbLatex/img/34c1bece1ebb81a11e7c22a2bca18076-1.gif) 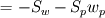 The partial derivative at the "bottom" face has on purpose not been approximated yet. I have two questions both with ideas that I hope can produce some comments. First, how do I approximate the pressure-gradient source at the inlet 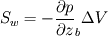 ? ?My first thought is to use linear extrapolation to determine the pressure outside the domain. Using central differences, I then arrive to: 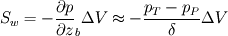 Should I use higher order extrapolation, or will this suffice? Second question, how do I approximate the velocity gradient? I would specify my velocity there as the inlet velocity 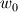 is known. I therefore approximate the remaining partial derivative as: is known. I therefore approximate the remaining partial derivative as: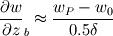 . . This approach would correspond to setting 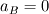 , , 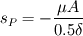 and and 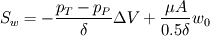 . .Looking forward for any input Regards, Johnhelt |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Hi Johnhelt,
I'm not an expert on CFD or SIMPLE-like algorithms, but for the past 9 months or so I've been modifying a code written for SIMPLER algorithm and have had to do some discretisations (for a 1-D grid though). I'm assuming that P here refers to the boundary grid point on the bottom surface. Also the 0.5 in your velocity gradient comes from the fact that you're looking at a half-cell. So if you look at the control volume along the z-direction you'd have P----t-----T where t is the face of the CV. So shouldn't the pressure gradient term be 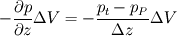 ? ?similarly for the other gradient terms because you integrate between the face of the CV. So for the grid along the x-direction W---w---P---e---E 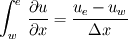 Now if you are looking at the boundary node P at the left-hand-side (LHS) you do not have u_w and u_w can be taken as the value of u_P, which is what you've done when you took w_0 for w_B. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 15  |
Hi Lost Identity, and thanks for your fast reply. I think I forgot to mention some nomenclature..
The distance between two nodal points is 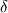 , so then the pressure gradient at P, following your notation, should then be: , so then the pressure gradient at P, following your notation, should then be: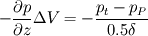 However, the pressure at the 't' face is not known (I'm using collocated variables). You can find it by interpolation 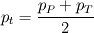 , and therefore you end up with , and therefore you end up with 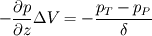 , which is the same as I wrote. So a boost of confidence there :-) , which is the same as I wrote. So a boost of confidence there :-)I'm not sure I get your integration though. At the "bottom" face: B----b----P----t----T after replacing volume integrals with surface ones by the Gauss theorem, the finite volume discretization at the b and t surface gives: 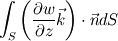 where 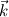 is the z-directional vector and is the z-directional vector and 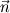 is the surface normal vector. Carrying out the dot product and integrating you get: is the surface normal vector. Carrying out the dot product and integrating you get: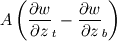 so I need to evaluate both gradients at the two surfaces, which can be done by central differences. However, at the bottom surface only 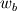 is known is known 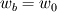 , while the velocity at B is unknown (outside of domain). When using linear interpolation the gradient at b , while the velocity at B is unknown (outside of domain). When using linear interpolation the gradient at b 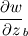 of course ends up being identical to that between b and P. of course ends up being identical to that between b and P.Regards! |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Hi,
Sorry I made a mistake in my integral, missed out the dx and also I was only thinking of 1-D in it. I think that's how I would do it too if I were you. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 15  |
Ok a follow-up for those who care...
I'm solving the Navier-Stokes equation for incompressible (laminar) flow to a hole in a plate - and inside that hole as well, where a parabolic flow profile should form. Later I will apply a permeability term to look at the effect of deposition from the flow (filtration). I have implemented the solution using the SIMPLE method with on a structured grid. The whole thing is solved using the preconditioned conjugate gradient method. With regards to the boundary conditions: If I use the approach I wrote in the original post, I get oscillations in the velocity near the inlet in the converged solution. These oscillations, however, die out a few grid points away from the inlet. Instead, I found that specifying the pressure-gradient 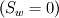 , as well as velocity gradient at the boundary , as well as velocity gradient at the boundary 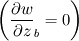 to 0 both, while specifying the velocity at the "bottom" face in the pressure-correction equation to the inlet velocity to 0 both, while specifying the velocity at the "bottom" face in the pressure-correction equation to the inlet velocity 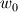 , I get the correct velocity field - without oscillations near the inlet. , I get the correct velocity field - without oscillations near the inlet.I guess it corresponds to specifying the velocity far from the domain, however I could not find any good explanation to this in Versteeg's book.. perhaps someone here can explain? Regards, JH |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| inlet and outlet boundary condition for turbomachinery solution | siamak1424 | OpenFOAM | 2 | August 15, 2009 11:14 |
| Question about pressure inlet boundary condition. | Alina | FLUENT | 1 | November 30, 2007 07:39 |
| Please help with flow around car modelling! | Tudor Miron | CFX | 17 | March 19, 2004 19:23 |
| inlet and outlet boundary condition of pump | Thammasak | CFX | 0 | February 9, 2004 13:02 |
| what the result is negatif pressure at inlet | chong chee nan | FLUENT | 0 | December 29, 2001 05:13 |