
 |
Solving k-e model
Hi, I am writing a code with FORTRAN to solve the k-e model. I have a Problem with the eddy viscosity formulation. The flow I like to predict is one over a rotating disc. This flow is considered to disappear in the infinty and so at the end of the grid (far away from the disc) too.
So k and e become zero far away from the disc....my problem is that in formulation of the eddy viscosity for the k-e model i have to calculate kČ/e....and this causes problems because k is in the infinity 1+10^-30 and e is 1*10^-33....so kČ/e is becoming something like 1000 but it should be zero. Has anybody an idea how I can solve this? Thanks! Alex |
Quote:
|
Dear Mr Ignat,
I have developed a 2d collocated pipe flow cfd code. I am trying to implement turbulence model into it (simple prandtl's mixing length model). But after implementation turbulence profile looks more peaky than the laminar profile at the exit. Can you suggest me some solution for this error. Thanks in advance |
Quote:
As I know prandtl's mixing length model is too rough. I recommend you to use Spalart-Allmaras model without ft2 term. Look here http://turbmodels.larc.nasa.gov/spalart.html It is simple one-equation model for one variable with no-problem boundary conditions. For pipe flows it gives good resuts. Be careful with boundary conditions for velocity at the wall. If closest cell size > then 10 (in wall units y+) you should use wall-function - logarithmic profile. |
Dear Mr ignat,
Thankyou for your message. One more doubt is that you said to be cautious at the wall boundary condition for velocity, confused whether to give the wall velocity zero or not. Actually from the log law layer expression are we finding the tou_w (wall shear stress) ? Can you please clear this doubt. Thanks |
Dear Mr Ignat
Extremely thankful for your reply. Can you please check the following procedure that i am going to implement in my laminar code Procedure pertaining to turbulence -------------------------------------- 1 Assume tou_w (wall shear stress) to some initial value 2 Then find y+ according to the formula y+ = row * ut * y/meu 3 Substitute this y+ value in the tou_w expression obtained from log-law layer Then add this tou_w to the momentum equation as a source term along with the dp/dx like this (neglecting ‘a s’ term) apUp=awUw+anUn+aeUe+(dp/dx) * volume + (tou_w x area) but for v momentum equation apVp=awVw+anVn+aeVe+asVs +(dp/dy)*volume Overall procedure as follows
|
1 Attachment(s)
Quote:
Is this algorithm your own invention? :) Sorry,but I think it does't work. Don't think up your own methods. Time is money. The better way is to study well known and robust methods for calculation of incompressible flows. I recommend you to use some staggered grid algorithm, for example this Kim, J., Moin, P., Application of Fractional-Step Method to Incompressible Navier-Stokes Equations. // J.Comp.Phys. 1985, v.59, pp. 308-323 or some others which use staggered grid, but not collocated one because for collocated grids there is a problem of pressure-velocity link. Some about boundary condition. I do the following way. In order to calculate 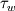 you should solve the equation: you should solve the equation: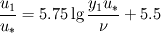 and find 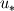 where where 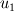 is known velocity at closest node, is known velocity at closest node, 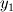 is the distance from the closest node to the wall and is the distance from the closest node to the wall and  is the molecular kinematic viscosity. is the molecular kinematic viscosity.This is transcendental equation and it is simply solved by Newton iterations with initial guess for 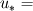 small value, for example 0.00001 small value, for example 0.00001Then 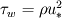 . (1) . (1)On the other hand 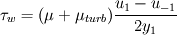 (2) (2)where 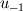 is the false velocity at the false node outside the domain which is placed at the same distance is the false velocity at the false node outside the domain which is placed at the same distance 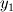 . From (1) and (2) you find . From (1) and (2) you find 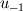 and use it as boundary condition for momentum equation. and use it as boundary condition for momentum equation.Look picture |
Quote:
Your variant is correct for OUTFLOW boundary only. |
Hi,
Thanks. I think you have mistaken me. It was just a outline only. Actually i have taken care of all those pressure-velocity coupling problems. Infact i had a systematic start in coding with 1d staggered solver then 2d staggered, 1d colocated and then 2d colocated. Now for this 2d colocated code i am trying to implement the turbulence model. (Basically mine is an incompressible flow solver). I will use your ideas to implement the boundary condition for the turbulence. thankyou jyothishkumar |
Hi jyothishkumar
It was really misunderstanding, sorry. That's ok.:) Best regards, |
Hi
Use Teach code as a pattern. Amir |
hi amir,
what is this Teach code. Is it something to tell about turbulence model implementation ? thanks jyothish |
Dear Mr Ignat,
I am trying with k epsilon turbulence implementation in my code (std k epsilon). I am just following the malalasekara book (latest edition) for this implementation. Or please tell me the ideas like what is the source term to be added in momentum eqn etc etc. how to handle the source term in k epsilon equation. Whether to solve for k equation for the first node or can i use directly like k = utou^2/sqrt(cmu). Thanks in advance jyothish |
Quote:
As I know standard k-e model is very stiff so both of equations have to be solved implicitly. Both k-equation source term and e-equation one must be linearized and approximated at n+1 time level. Moreover, diffusion terms in both equations have to be solved implicitly too. This way usually can avoid negative k & e values. wish good luck. |
Prandtl mixing length implementation
Hi everyone,
I have succesfully created a solver in Matlab for 2d STEADY incompressible Poiseulle flow, using a backward staggered grid, FVM, SIMPLE algorithm and hybrid differencing scheme, with good results to Hagen-Poiseulle velocity profile. Boundary conditions are inlet-outlet, with the walls being brought into the domain the wall shear stress, (I have stuck rigidly to Versteeg). I am now at the stage of adding turbulence models. I understand from Patankar, that it is best to leave out the Reynolds stress terms in the momentum equations explicitly, but to the use the effective viscosity, which is the dynamic + turbulent. (mu_eff =mu + mu_t). Turbulence modelling: In the RANS and 2D flow, the only relevant reynold stress is tau_xy, which we then discretise -d(tau_xy)/dy for a cell volume, i.e. (tau_xy*A)n - (tau_xy*A)s, where n & s are the north and south FACES, and tau_xy, for the Prandtl mixing length is: rho*mixing_length^2*du/dy^2. Again, du/dy is ((u)n - (u)s)/deltayp. Similarly for the v-momentum, except now (tau_xy*A)e - (tau_xy*A)w.... du/dy is still the same. I feel ashamed having to ask about discretisation! lol! I just want to be sure and do not have time for second guessing myself!! :( mixing length for pipe flow is L[0.14-0.08(1-y/L)^2 - 0.06(1-y/L)^4], where y is the distance from the node to the wall , L is the radius/ half channel width. Therefore, for each u- and v- cell, i must calculate: 1. the mixing length, with y being the distance from the wall to the u-cell centre 2. the velocity gradient ((u)n - (u)s)/deltayp, where the value of (u)n or (u)s will be linearly approximated by, e.g. (u)n = (u(i,J) + u(i,J+1))/2 3. 1 & 2 allows me to calculate tau_xy 4. now, to get the value of tau_xy at cell faces, use central differencing? 5. along wall nodes, do i use u+ instead of up to calculate the shear stress and add it in the source serm b? It is SUPPOSED to be quick and easy to implement... so I appreciate any assistance. following this, i want to add k-epsilon Best regards, Michael 0565113@gmail.com |
Quote:
|
| All times are GMT -4. The time now is 20:08. |