
 |
maybe I'm misunderstanding you, but the classical RK schemes use stages/nodes that are INSIDE the interval you are trying to integrate....so you are integrating in time, and you need the evaluation at (say) 1/3 delta t, 1/2 delta t, 2/3 delta t and so on...
how you discretize your spatial domain is up to you, since you are using a method of lines approach.... |
Dear cfdnewbie
Thank you for your reply. Would please review my spreading out of the equations. 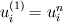 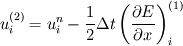 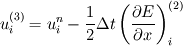 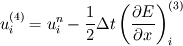 ![u^{n+1}_{i} = u^{n}_{i} - \Delta t \left[
\frac{1}{6} \left( \frac{\partial E}{\partial x} \right)^{(1)}
+
\frac{1}{3} \left( \frac{\partial E}{\partial x} \right)^{(2)}
+
\frac{1}{3} \left( \frac{\partial E}{\partial x} \right)^{(3)}
+
\frac{1}{6} \left( \frac{\partial E}{\partial x} \right)^{(4)}
\right] u^{n+1}_{i} = u^{n}_{i} - \Delta t \left[
\frac{1}{6} \left( \frac{\partial E}{\partial x} \right)^{(1)}
+
\frac{1}{3} \left( \frac{\partial E}{\partial x} \right)^{(2)}
+
\frac{1}{3} \left( \frac{\partial E}{\partial x} \right)^{(3)}
+
\frac{1}{6} \left( \frac{\partial E}{\partial x} \right)^{(4)}
\right]](/Forums/vbLatex/img/c0015a9a4d425457abbddbd7b6910231-1.gif) Becasue 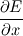 is defined as is defined as 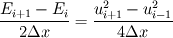 , ,  refers refers  . .And, in turn, 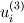 refers refers 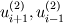 . . Here, 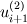 comes from comes from 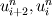 and and 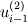 is derived from is derived from 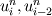 . . As a result, to get 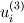 , I need the values of , I need the values of 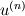 at i+2~i-2. at i+2~i-2. As the same manner, 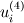 requires the value of requires the value of 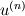 at i-3~i+3. at i-3~i+3. I feel that something is wrong with my equations but I'm in trouble to figure out it cleary. I attached my F90 code for fixing..(it works any way) I appreciate that again. |
dear cfdnewbie
I understood my problem. my original program was... DO i=2,IM-1 u1(i) = function of u(n,i) u2(i) = function of u(n,i) u3(i) = function of u(n,i) u4(i) = function of u(n,i) END DO but the right one should be DO n=1,NM-1 DO i=2,IM-1 u1(i) = function of u(n,i) END DO DO i=2,IM-1 u2(i) = function of u1(i) END DO DO i=2,IM-1 u3(i) = function of u2(i) END DO DO i=2,IM-1 u4(i) = function of u3(i) END DO DO i=2,IM-1 u(n+1,i) = u(n,i) + ~~~ END DO END DO at first i tred to write all u1, u2, u3, u4 as functions of u(n) along just one iteration, but now there are each iteration for u1~u4, and in another iteration I calculate u(n+1) |
| All times are GMT -4. The time now is 13:18. |