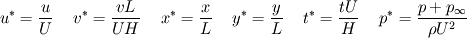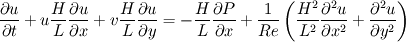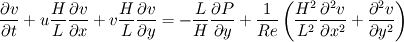CFD Online Discussion Forums - Lid driven flow in shallow rectangular domain issues, MATLAB

So i'm modifying the code made by Benjamin Seibold to deal with shallow rectangular cavities for lid driven flows. Original code is located here and is 6.7 under MATLAB codes along with associated documentation.

http://www-math.mit.edu/cse/

My problem is that the pressure correction step is not enforcing a divergence free velocity field.

To change to a rectangular domain, I have non dimensionalized using the following:

$u^* = \frac{u}{U}\hspace{5 mm} v^* = \frac{vL}{UH} \hspace{5 mm} x^* = \frac{x}{L} \hspace{5 mm}y^* = \frac{y}{L} \hspace{5 mm} t^* = \frac{tU}{H} \hspace{5 mm} p^* = \frac{p + p_\infty}{\rho U^2}$

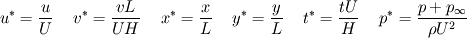
which gives the N-S equations

$\frac{\partial u}{\partial t} + u \frac{H}{L} \frac{\partial u}{\partial x} + v \frac{H}{L} \frac{\partial u}{\partial y} = -\frac{H}{L} \frac{\partial P}{\partial x} + \frac{1}{Re}\left( \frac{H^2}{L^2} \frac{\partial ^2 u}{\partial x^2} +\frac{\partial ^2 u}{\partial y^2} \right)$

$\frac{\partial v}{\partial t} + u \frac{H}{L} \frac{\partial v}{\partial x} + v \frac{H}{L} \frac{\partial v}{\partial y} = -\frac{L}{H} \frac{\partial P}{\partial y} + \frac{1}{Re}\left( \frac{H^2}{L^2} \frac{\partial ^2 v}{\partial x^2} +\frac{\partial ^2 v}{\partial y^2} \right)$

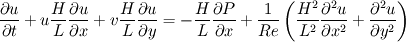
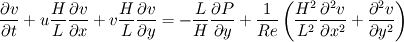
Here is the modified code that I have so far. It plots the stream lines, the u and v velocity at different vertical slices of the rectangle and prints the maximum divergence in the field.

if you feel like running it, just copy paste to matlab m file, save and hit F5 and everything should work. By adjusting AR at the top, you can change the size of the rectangle where AR = H/L

If the AR is 1, code runs fine and quantitative values have been compared with ghia and do not show any significant errors. Any one know whats wrong??????

Thanks

Code:

function []=debug()



clear all

close all

clc



%% Paramters

AR=0.5;                                        % Aspect Ratio

Pe=500;                                      % Peclet Number

Re = 100;                                    % Reynolds number

tf = 40e-0;                                  % final time

dt = 0.01;                                   % time step

lx = 1;                                      % width of non-D domain

ly = 1;                                      % height of nond-D domain

hxmax=0.025;                                  % Maximum x grid size

hymax=0.025;                                  % Maximum y grid size

ny=ceil(1/hymax);                            % Number of y grid points

nx=ceil(1/AR/hxmax);                         % Number of x grid points

hy=1/ny;                                     % Actual y grid size

hx=1/nx;                                     % Actual x grid size

% Dimensional Variables

H=1;                                       % Height of droplet

L=H/AR;                                      % Length of droplet

dy=H/ny;                                     % Width of y grid

dx=L/nx;                                     % Width of x grid

dimx(1:nx+1)=(0:nx)*dx;                      % X coordinates

dimy(1:ny+1)=(0:ny)*dy;                      % Y coordinates

% Fluid Properties

rho=1000;                                    % Density

mu=0.86e-3;                                  % Viscosity

c=4184;                                      % Specific heat

k=0.6;                                       % Thermal conductivity

ubulk=(Re*mu)/(rho*H);                       % Bulk Velocity

nsteps = 10;  % number of steps with graphic output

%-----------------------------------------------------------------------



nt = ceil(tf/dt); dt = tf/nt;                % number of time iterations



x = linspace(0,lx,nx+1);                     % non-D x coordinates

y = linspace(0,ly,ny+1);                     % non-D y coordinates

[X,Y] = meshgrid(y,x);

%-----------------------------------------------------------------------

% initial conditions

U = zeros(nx-1,ny); V = zeros(nx,ny-1);

% boundary conditions

uN = x*0+1; uN = [0 uN(2:end-1) 0];

uS = x*0; uS = [0 uS(2:end-1) 0];

uW = avg(y)*0;

uE = avg(y)*0;



vN = avg(x)*0;

vS = avg(x)*0;

vW = y*0;

vE = y*0;

%% Time stepping



Ubc = dt/Re*([2*uS(2:end-1)' zeros(nx-1,ny-2) 2*uN(2:end-1)']/hy^2+...

      [uW;zeros(nx-3,ny);uE]/hx^2);

Vbc = dt/Re*([vS' zeros(nx,ny-3) vN']/hy^2+...

      [2*vW(2:end-1);zeros(nx-2,ny-1);2*vE(2:end-1)]/hx^2);



fprintf('initialization')

Lp = kron(speye(ny),AR*K1(nx,hx,1))+kron((1/AR)*K1(ny,hy,1),speye(nx));

Lp(1,1) = 3/2*Lp(1,1);

perp = symamd(Lp); Rp = chol(Lp(perp,perp)); Rpt = Rp';

Lu = speye((nx-1)*ny)+dt/Re*(kron(speye(ny),AR^2*K1(nx-1,hx,2))+...

     kron(K1(ny,hy,3),speye(nx-1)));

peru = symamd(Lu); Ru = chol(Lu(peru,peru)); Rut = Ru';

Lv = speye(nx*(ny-1))+dt/Re*(kron(speye(ny-1),AR^2*K1(nx,hx,3))+...

     kron(K1(ny-1,hy,2),speye(nx)));

perv = symamd(Lv); Rv = chol(Lv(perv,perv)); Rvt = Rv';

Lq = kron(speye(ny-1),K1(nx-1,hx,2))+kron(K1(ny-1,hy,2),speye(nx-1));

perq = symamd(Lq); Rq = chol(Lq(perq,perq)); Rqt = Rq';



fprintf(', time loop\n--20%%--40%%--60%%--80%%-100%%\n')

for k = 1:nt

   % treat nonlinear terms

   gamma = min(1.2*dt*max(max(max(abs(U)))/hx,max(max(abs(V)))/hy),1);

   Ue = [uW;U;uE]; Ue = [2*uS'-Ue(:,1) Ue 2*uN'-Ue(:,end)];

   Ve = [vS' V vN']; Ve = [2*vW-Ve(1,:);Ve;2*vE-Ve(end,:)];

   Ua = avg(Ue')'; Ud = diff(Ue')'/2; 

   Va = avg(Ve);   Vd = diff(Ve)/2;

   UVx = diff(Ua.*Va-gamma*abs(Ua).*Vd)/hx;

   UVy = diff((Ua.*Va-gamma*Ud.*abs(Va))')'/hy;

   Ua = avg(Ue(:,2:end-1));   Ud = diff(Ue(:,2:end-1))/2;

   Va = avg(Ve(2:end-1,:)')'; Vd = diff(Ve(2:end-1,:)')'/2;

   U2x = diff(Ua.^2-gamma*abs(Ua).*Ud)/hx;

   V2y = diff((Va.^2-gamma*abs(Va).*Vd)')'/hy;

   U = U-dt*AR*(UVy(2:end-1,:)+U2x);

   V = V-dt*AR*(UVx(:,2:end-1)+V2y);

   

   % implicit viscosity

   rhs = reshape(U+Ubc,[],1);

   u(peru) = Ru\(Rut\rhs(peru));

   U = reshape(u,nx-1,ny);

   rhs = reshape(V+Vbc,[],1);

   v(perv) = Rv\(Rvt\rhs(perv));

   V = reshape(v,nx,ny-1);

   

   % pressure correction

%    rhsv = reshape((diff([uW;U;uE])/hx+diff([vS' V vN']')'/hy),[],1);

%    rhsv = rhsv.*AR^2;

%    rhsu = reshape((diff([uW;U;uE])/hx+diff([vS' V vN']')'/hy),[],1);

%    pu(perp) = -Rp\(Rpt\rhsu(perp));

%    pv(perp) = -Rp\(Rpt\rhsv(perp));

%    Pu = reshape(pu,nx,ny);

%    Pv = reshape(pv,nx,ny);

%    U = U-AR*diff(Pu)/hx;

%    V = V-(1/AR)*diff(Pv')'/hy;

   

   rhs = reshape(diff([uW;U;uE])/hx+diff([vS' V vN']')'/hy,[],1);

   p(perp) = -Rp\(Rpt\rhs(perp));

   P = reshape(p,nx,ny);

   U = U-diff(P)/hx;

   V = V-diff(P')'/hy;

   

   % visualization

   if floor(25*k/nt)>floor(25*(k-1)/nt), fprintf('.'), end

   if k==1|floor(nsteps*k/nt)>floor(nsteps*(k-1)/nt)

      % stream function

      rhs = reshape(diff(U')'/hy-diff(V)/hx,[],1);

      q(perq) = Rq\(Rqt\rhs(perq));

      Q = zeros(nx+1,ny+1);

      Q(2:end-1,2:end-1) = reshape(q,nx-1,ny-1);

%       clf, contourf(avg(x),avg(y),P',20,'w-'), hold on

      contourf(dimx,dimy,Q',20,'w-');

      Ue = [uS' avg([uW;U;uE]')' uN'];

      Ve = [vW;avg([vS' V vN']);vE];

      Len = sqrt(Ue.^2+Ve.^2+eps);

%       quiver(x,y,(Ue./Len)',(Ve./Len)',.4,'k-')

      hold off, axis equal, axis([0 L 0 H])

%       p = sort(p); caxis(p([8 end-7]))

      title(sprintf('Re = %0.1g   t = %0.2g',Re,k*dt))

      drawnow

   end

end

fprintf('\n')



ufield=Ue';

vfield=Ve';



ulab=abs(ufield-1);



mid=ceil((nx+1)/2);

quart=ceil(1*(nx+1)/100);

if quart==1

    quart=2;

end



third=ceil(5*(nx+1)/100);

next=ceil(1*(nx+1)/5);

figure(3)

plot(ulab(:,quart),y,ulab(:,third),y,ulab(:,next),y,ulab(:,mid),y)%,ulab(:,end-quart),y)

legend('0.02H','0.1H','0.4L','H','other','location','West')

title('U profiles')



figure(4)

plot(vfield(:,quart),y,vfield(:,third),y,vfield(:,next),y,vfield(:,mid),y)%,vfield(:,end-quart),y)

legend('0.02H','0.1H','0.4L','H','other','location','West')

title('V profiles')



%% Divergence Test

div=divergence(ufield,vfield);

max_div = max(max(div(2:end-1,2:end-1)))



function B = avg(A,k)

if nargin<2, k = 1; end

if size(A,1)==1, A = A'; end

if k<2, B = (A(2:end,:)+A(1:end-1,:))/2; else, B = avg(A,k-1); end

if size(A,2)==1, B = B'; end



function A = K1(n,h,a11)

% a11: Neumann=1, Dirichlet=2, Dirichlet mid=3;

A = spdiags([-1 a11 0;ones(n-2,1)*[-1 2 -1];0 a11 -1],-1:1,n,n)'/h^2;