 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Vincent
Join Date: Jul 2011
Posts: 29
Rep Power: 14  |
This post is in response to a message I recieved of someone that wanted to have a more detailed explanation on how to obtain the non-dimensional NS equations. Since others might be interested (and the fact that I like this tex compiler) I posted on this forum.
For starters we introduce the Navier Stokes equations and look at the x-direction component: 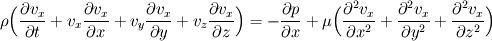 We assume no additional body forces. The components of the velocity field v are denoted by subscripts (x,y,z). The pressure is given by p and 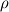 is the density. is the density.First we divide by the density  in order to simplify the equation. in order to simplify the equation. The reader should check that indeed each terms has a dimension equal to 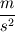 . Now in order to obtaint the non-dimensional equation we make the following substitutions. . Now in order to obtaint the non-dimensional equation we make the following substitutions.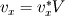 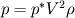 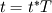 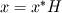 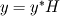 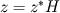 Quantities with a superscript star are dimensionless quantities and the capital letters V and H have dimensions  and and 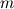 respectively. respectively. Please check that these substitutions are indeed valid. For instance the physical length is 4 m. We decide to take the length H equal to 1 m, giving a non-dimensionalised length of 4. Using the above substitutions we end up with the following equation: 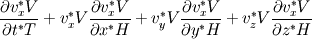 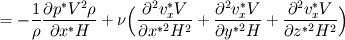 We simplify this equation and use that T = H/V. 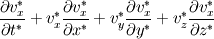 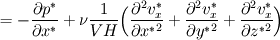 Here 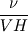 is our inverse reynolds number. is our inverse reynolds number.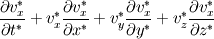 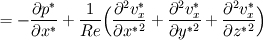 Where Re is defined as 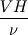 . Now we have non-dimensionalised the NS equations. Please rememeber that if you solve this equation you will end up with the nondimensionalised quantities. In order to revert them to physical quantities you will need to use the equation we proposed above when we non-dimensionalised the quantities. . Now we have non-dimensionalised the NS equations. Please rememeber that if you solve this equation you will end up with the nondimensionalised quantities. In order to revert them to physical quantities you will need to use the equation we proposed above when we non-dimensionalised the quantities.Good luck! Regards, Vincent |
|
|
|

|
|
|
|
|
#3 |
|
New Member
wuzj
Join Date: Mar 2011
Posts: 6
Rep Power: 15  |
if there are force term in the NS equation, how to deal with it??
for example, when use the immersed boundary method to solve the flow past fixed circular, what should i do with the force term nondimension??? |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Vincent
Join Date: Jul 2011
Posts: 29
Rep Power: 14  |
In the case of an additional body force (like gravity) the equation changes to include an additional term.
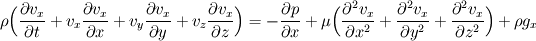 Again dividing by 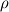 yields this term indeed as an acceleration yields this term indeed as an acceleration  . .If we then substitute in the following way: 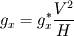 We end up with the following equation: 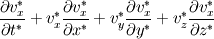 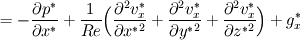 So for instance if we want to simulate gravity where 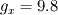 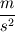 . Then we first determine . Then we first determine 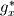 by multiplying by H and dividing by by multiplying by H and dividing by 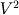 . .For instance, let's say we took H = 0.4 m and V = 2 m/s, this gives that 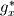 is equal to 9.8*0.4/4 is 0.98. is equal to 9.8*0.4/4 is 0.98.Good luck! Regards, Vincent |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Vincent
Join Date: Jul 2011
Posts: 29
Rep Power: 14  |
A simple immersed boundary method can be implemented in the following way. The philosophy behind the idea is that we will determine the fluid flow without the obstacle and the in a next step force the fluid flow to zero using a body force.
Introducing a phase indicator function 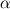 that can either be one (solid-phase) or zero (fluid-phase). By multiplying our body force with this phase indicator function we only imply a force where our obstacle is. that can either be one (solid-phase) or zero (fluid-phase). By multiplying our body force with this phase indicator function we only imply a force where our obstacle is.However we can't use a simple constant for the forcing term 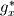 since we want this opposing force to set the velocity exactly to zero and not a positive or negative value. since we want this opposing force to set the velocity exactly to zero and not a positive or negative value.So we need a parametrization for our body force. The forcing in a certain cell can be expressed in the following form: 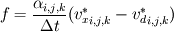 Here 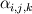 is our phase indicator function as defined above. is our phase indicator function as defined above. 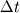 is our numerical timestep is our numerical timestep 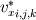 the velocity in a certain cell at the current timestep before forcing. Our desired velocity is the velocity in a certain cell at the current timestep before forcing. Our desired velocity is 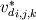 which is equal to zero in the case of a solid. Combining these elements gives that our full equation: which is equal to zero in the case of a solid. Combining these elements gives that our full equation: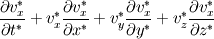 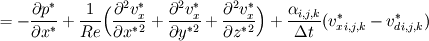 Now we need to supply a geometry field ( 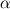 ) and the desired velocity field (which for simple cases will be zero everywhere). ) and the desired velocity field (which for simple cases will be zero everywhere).Good luck! Regards, Vincent |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Astio Lamar
Join Date: May 2012
Location: Pipe
Posts: 186
Rep Power: 13  |
Dimensionless Navior-Stoks in cylindrical coordinate :
 non-dimensional parameters which we use here:  for r-component we have:  Last edited by asal; May 3, 2012 at 10:35. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Astio Lamar
Join Date: May 2012
Location: Pipe
Posts: 186
Rep Power: 13  |
for theta-component, we have:
 and finally for z-component, we have: 
|
|
|
|

|
|
|
|
|
#8 |
|
Member
Osman
Join Date: Oct 2012
Location: Japan
Posts: 53
Rep Power: 13  |
Hi VincentD, could you tell me how to choose V and H ???
|
|
|
|

|
|
|
|
|
#9 |
|
New Member
teja
Join Date: Nov 2013
Posts: 2
Rep Power: 0  |
Hi,
I need to non dimensionalize energy equation of navier stokes. Can you help me out |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Ahmed Aql
Join Date: Aug 2015
Location: Kuwait
Posts: 4
Rep Power: 10  |
Please, Thank you for the great explanation. I have a question, how didn't you non-dimensionalized theta?! and is it okay to express the azimuthal (tangential) velocity with the same reference parameter as the axial and radial velocities? thank you!
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
theta is not dimensionally homogeneous to a lenght that needs to be non-dimensionalized but it is an angle position (rad).
|
|
|
|

|
|
|
|
|
#12 |
|
New Member
Ahmed Aql
Join Date: Aug 2015
Location: Kuwait
Posts: 4
Rep Power: 10  |
Thank You! but what will be wrong with the below dimensionless parameters?
I considered theta as a reference variable to dimensionalize the tangential coordinate I also expressed the tangential dimensionless velocity considering the angular velocity as a reference variable. 
|
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
No, theta ranges from 0 to 2*pi is already a non-dimensional number, furthermore, the velocity reference is unique |
||
|
|

|
||
|
|
|
#14 | |
|
New Member
Ahmed Aql
Join Date: Aug 2015
Location: Kuwait
Posts: 4
Rep Power: 10  |
Quote:
I can see now how theta is already dimensionless. I am still a little bet confused about how the tangential velocity can be expressed in terms of a the unique reference velocity (Vr) which has [ L / T ] dimensions while omega r have a dimension [ T ^-1] ? Thank you so much |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
|
||
|
|

|
||
|
|
|
#16 |
|
New Member
Ahmed Aql
Join Date: Aug 2015
Location: Kuwait
Posts: 4
Rep Power: 10  |
||
|
|

|
|
|
|
|
#17 |
|
New Member
Adarsh Choudhury
Join Date: Jul 2017
Posts: 1
Rep Power: 0  |
How to non dimensionalise if we have to include surface tension and obtain Capillary number in the final equation
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Filtered navier stokes equation..LES:: | Palani Velladurai | Main CFD Forum | 7 | September 6, 2013 02:51 |
| Adding a term to Navier Stokes Equation | ashtonJ | CFX | 3 | January 15, 2011 06:32 |
| Navier stokes compresible viscid flow fea, somebody can help? | Jose Choy | Main CFD Forum | 3 | October 24, 2003 02:28 |
| Newbie:Viscoelasticity and Navier stokes equation | Rajil Saraswat | Main CFD Forum | 2 | June 9, 2003 07:21 |
| help: I am trying to solve Navier Stokes compressible and viscid flow | Jose Choy | Main CFD Forum | 2 | May 18, 2000 05:45 |