CFD Online Discussion Forums - expandableInterFoam

Hi guys,

I'm working on a modification of the interFoam solver that considers isobaric expansibility of both phases.

So my modified VOF and pressure correction equations look like:
$\frac{\partial{\alpha_1}}{\partial{t}}+\nabla\cdot \left( \alpha_1 \vec{u}_1 \right) =Su_{\alpha_1}$
$\nabla \cdot \left( \left( \frac{1}{A_D} \right)_f \nabla_f p \right)=\nabla \cdot \vec{u}^* + Su_p$
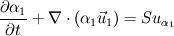
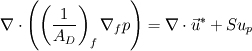
where 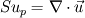$Su_p=\nabla \cdot \vec{u}$ is velocity divergence computed from the continuity equation.

The problem with this formulation is, that it is not conservative and requires consistent and accurate calculation of the source terms 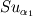$Su_{\alpha_1}$ and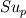

. For now it works fine within in each phase, but I still have considerable mass imbalance in the interface region.

The second formulation I try to implement is a conservative one. VOF equation works well:
$\frac{\partial{(\alpha_1 \rho_1)}}{\partial{t}}+\nabla\cdot \left( \alpha_1 \rho_1 \vec{u}_1 \right) =0$

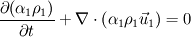
But I get pressure-velocity-oscillations if I solve following pressure correction equation:
$\nabla \cdot \left( \left( \frac{1}{A_D} \right)_f \rho_f \nabla_f p \right)=\nabla \cdot \left( \rho \vec{u} \right)^* + Su_p$
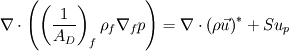
with 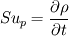$Su_p=\frac{\partial \rho}{\partial t}$

It looks like the classical chessboard problem (cartesian mesh), which I thought shouldn't be there because of the Rhie&Chow-like discretization of pressure. And that's actually my question to you: why does it happen and how could I prevent it?

Can anyone help me with a smart advice?

Best regards,
Ilya