
 |
InterFoam: Add an equation to only one phase
1 Attachment(s)
Hello again everybody,
as I already explained here, I want to insert a tracer in my simulation to calculate the mixing time of the reactor. I want to consider only the liquid phase as I am going to insert a certain amount of NaCl as tracer and follow the time evolution of the concentration with a probe. Now I was just able to add the tracer using as a base the wiki page on how to add temperature to icoFoam. However, if I run the simulation I get my tracer propagating out of the liquid phase through the interface into the gas. Watching this thread (http://www.cfd-online.com/Forums/ope...interfoam.html) I made an idea of how to read physical properties for different phases but I cannot figure out how to make my equation to be solved only for the liquid phase. To put things simple, now it looks like it is just overlapping the liquid-gas system (i have a global equation, a global diffusion coefficient, etc). See attached screenshot (tracer concentration profile on the right). Is there anybody who can help me with this task? Thanks! |
Did you try to determine the diffusion coefficient based on the liquid fraction alpha1? There is no way to solve an equation for only one of the phases using interFoam.
|
Quote:
thank you for the precious hint! I thought that the equations were solved for both the phases... but then, where the alpha1 parameter meaning goes?? So, you are right and I should take that into account, which brings us (me) to a big problem... I don't have any idea on how to modify the C++ code. I tried to add alpha1 in the ::div and ::ddt functions but they seem to be programmed to accept only 2 arguments, hence I need to define a new variable (or a function) which already incorporates the calculations. It is such a simple task (a matter of multiplying, summing and subtracting) but I don't know how to implement it in the code. I also tried copy/pasting other functions (also from the thread mentioned above) but to no avail. I'm stuck (again). Thanks! |
For the implementation you have linked some threads for the temperature implementation, which will be similar. However, you will probably not be able to keep all the concentration in the liquid phase only by numerical diffusion. This is a complicated issue, which is probably described in literature a lot.
|
bernhard is right, there is no way :), to solve your equation just for one phase
but to reduce numerical diffusion, in each time step you should update your concentration with alpha1 |
@Bernhard
I was already aware of that.... or at least I was imagining that such a behaviour could cause problems. @nimasam I would like to do that but I lack the ability to create functions, define new variables or manipulate existing ones. To put it simple, I don't know C++...:confused: Copy/pasting a tutorial and adapt it to the new solver is on thing; to write your fuctions is another. Regarding the diffusion problems... well, my aim in this study is to model a phtobioreactor to assess whether a swirling flow arises and if it does, to calculate the frequency. This is not something like, you create your model, you implement it and then validate it through experiments. It is the reverse: I would like to explore different reactor configurations and when I find the good one, I will build it and see if the effect is the one that I expect. For this task the standard interFoam suffices and performs perfectly (I am already writing a paper with the validated results). The mixing time issue is something I would like to add in the workflow as I suspect that it can be used as a significant parameter... not sure though. However, I expect a Tmix of more than 1 minute so, the small effect of the diffusion between phases can become relevant. Just need to test it... If somebody knows how I can multiply my concentration for alpha1 before executing the divs and ddts I would be very grateful. for those who know C++ should be a trivial task... Tnks! |
Quote:
|
Quote:
The equation I would like to implement is really basic: if I neglect the diffusion (as the coefficient is 10^-9 order): d(rho*c)+div(rho*c*u)=0 which in OF should translate to: fvm::ddt(rho, c) + fvm::div(rho, c, U) If I get it right. Now I guess that if you don't take into account alpha1, interFoam just solves the eq for the continuum.... The first problem here is that "div(rho, c, U)" is not recognized and the compialtion fails (I don't have the trace as I am already at home). If I remove c or U (ie I leave only two terms) the file compiles. So, here I would like to add the alpha1 dependence in these derivatives but, as they only accept a limited number of parameters I suppose I should assign the calculations to another variable and than pass it to the main equation. For example: CAlpha == c*alpha1 CAlphaRho == CAlpha*rho and then: fvm::ddt(rho, CAlpha) + fvm::div(CAlphaRho, U) This should work (should get c=~0 for the gas and solve normally when alpha1=~1). Of course this code does not compile, complaining that neither CAlpha nor CAlphaRho have been declared for this scope. As I don't know how to define variables and subsequently how to use them in calculations, I don't know how and where to insert which code. Sorry for even not being able to better explain the situation... |
If you want to have convection of terms, you need the velocity at the phases, so you could use div(phi,c) or div(phiRho,c) (see http://openfoamwiki.net/index.php/Ma...ver_is_writing )
Some strange things are happening if you are defining CAlpha == c*alpha1. You should try to get your solver correct without these steps, and thus solving for c like you solve for T. As you only have convection, physically, as there is no mass flowing across the interface, you will also have no transport of c. Then you could try to multiply c after the solution step by alpha1 ( c *= alpha1 ), but I don't know how this will work out, and at least some concentration will be lost. |
Quote:
Quote:
Code:
Loosing some of the concentration in the multiplication step may be a minor drawback (I can look for a constant asymptotic value for the concentration and then normalize to the max). If the solver "eats" some of the concentration for each step, I will never get an asymptotic value though.... I will test this solution tomorrow. I hope this fix will work! Bernhard, thank you so much for your time! |
A possible solution, though it is a bit of a dodgy method, would be to add in the lost concentration in each timestep.
You could do this by checking in each timestep what the difference between the initial concentration and the current concentration is. The difference is the amount lost to numerical diffusion and you could add this back into your domain. For example by elevating all cell concentrations by an equal amount, but this might give you a small artificial increase of mixing speed (this is actually the same as your normalization). The other, probably more physical, option is to add the concentration at the interface (so in cells where 0<alpha1<1) because that is the location where the concentration is lost as well. Again: this is not at all a physical way of dealing with it, but since the numerical diffusion is unphysical as well you might get away with a solution of this kind. |
1 Attachment(s)
Quote:
Regarding the lost concentration, I am afraid that this may be a major problem. I was quite optimistic but looking at the results, I changed my mind. I saw 10 ml of 1 g/l solution dilute to 1 mg/l when the tracer did't occupy more than one third of the total volume (1 liter). This means it should dilute up to 1/30th, more or less but it almost vanished (1 mg/l). This comes from the fact that the bubbles moving through the tracer plume tend to "eat" it like a worm while the liquid should open and close leaving the bubble pass over instead. You can see three bubbles I evidenced in a screenshot I attach. This brings us to what michielm said: Quote:
Your first suggestion to blindly add back the lost concentration does not fits well my way of seeing the problem: if I add back the deltaC in each time step, the actual concentration drop due to the mixing gets lost in the process and I will end up with a constant profile. Or maybe I didn't get your point right. However this is a really sexy statement: Quote:
I spent some time in thinking about this and I came to an idea which I will try to explain to see what you think about that. Hope not to sound naive ;) First of all we have the same equation I compiled (with the alpha1 inclusion) solved to obtain the concentration and then we multiply for alpha1: Code:
solve(CEqn) ----> C'(t) ----> C'(t)*alpha1 = C(t)The tracer amount that vanishes in the time step (compared with the overall mass balance) should be then added back in the domain as michielm noted. At this point, adding it blindly in the domain (in every cell the same amount) will only screw things up... so I thought: what if I was able to sum the tracer back only in those cells where alpha1>0.5? And, wouldn't be nice to be able not to add anything back where alpha1=1 (i.e. do not artificially increase the max concentration)? So I schematized the interface situation like this: That's the profile of the interface and thus the profile of the concentration C after the multiplication. The part that's removed by alpha1<0.5 is the one that vanishes. So, I was wondering if it was possible to add it back in the blue dashed zone. Again, I don't want to add it back blindly, otherwise my C value in the alpha1=1 zone would get bigger than before the correction! So I am planning to use a sort of weighting system based on alpha1, using something like a gaussian profile like the one shown here: First you check whether the alpha1 value is grater than 0.5 and then you do your final correction basing on the profile of that curve: Of course you loose more then what you put back in the domain but at least you add it back to the right place. This is more or less what I was thinking to do... what do you think about it? And of course, how do I implement it without screwing up the code? Thank you and sorry for the long post! |
This is certainly an approach to keep the total mass of concentration at the end of each time step constant. However, there is no physical argument at all why you should do this. Your actually correcting the concentration with alpha purely. By the way, is the mass balanced without this correction? Now you want to partially undo this with a complicated approach. You can also think of multiplying with a function looking like Heaviside(alpha1-0.5), which will be doing something better already. Maybe this is what you are planning to do already? Also, you can never assume alpha1 across the interface anti-symmetric, so it will never be an optimal solution.
But please, do not try to solve this problem independently. I am quite convinced that people have been looking for solutions to this issue already quite a few times. Search in literature to find out what has been done, and compare the results of different approaches. This problem will take you a long time to solve, and then to only find out that it has been done in the 1990s will be frustrating: Have a look into how the interface is kept sharp in interFoam. Some artificial interface compression scheme is often used. Maybe it is possible to use this artificial convection in your equations as well, as it will keep the concentration away from the interface. Good luck, it is going to be tough :) |
Quote:
By the way, if I do directly multiplying by alpha1, the result is not mass balanced. And I dare to say it is badly unbalanced. Quote:
Quote:
Meanwhile thanks for your helpful support! |
hello,
You may take a look at the two Phase Euler solver ... if your case is applicable for Euler-Euler, then it will be easier to solve your scalar trough one phase only. If you stay with VOF, you may try to add 2 scalar instead of one, and balance from a <-> b depending of alpha: you will be conservative for (a,b), then it should be easier to rebalance your scalar at interface, and stay conservative. regards, olivier |
Quote:
Unfortunately I have tried the Euler-Euler solver many times and no matter what I do and how I initialize the domain, I never end up with a realistic fluid patter. Not to mention the gas hold-up. So I was forced to leave it for the more complicated (and time consuming) VOF. At least this one reproduces the behavior of my bubble column / air-lift system flawlessly. Quote:
Then? How do I balance from a to b using alpha? Thanks a lot. Luca |
hello !
What about the thermodynamic equilibrium at the interface ? According to your figure you have a partitioning at the gaz/liquid interface. Have you read this topic http://www.cfd-online.com/Forums/ope...interface.html ? You can also adapt the example to an equilibrium concentration at the interface and solve only the diffusion in one phase. (it is the single way to uncouple the equations in both phases) Regards, Cyp |
Quote:
Thanks a lot for the post you linked! That looks like the perfect solution! Defining C on the whole domain and then apply the derivatives was actually something I thought about but definitely not in the way you wrote there. That actually makes sense and moreover should be what I am looking for! I just have to find a proper model to fit the interface... using H does not fit as I want C in the gas strictly =0 (H= infinite, right?). Will think about that but meanwhile let me thank you for putting me on the (probably) right track! Luca |
Hello Cyp, and thanks for the development of the equations!
Taking another way I got to the same result but in my case it was inserted in the context of the equation I shown some posts above. I left it untouched (by actually removing diffusion) as I was not able to compile the file with my poor C++ knowledge. But let's say we can do like you kindly calculated and we end up with the equation (no flux at the interface): This represents the interfacial jump condition however I can leave it untouched as a function of 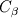 right? right?Now I should add it to the main equation to take into account the time dependence: 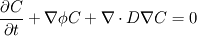 which, applying your calculations, should become: 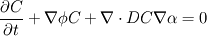 But the 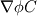 part should be treated the same way to include the alpha dependence right? Or am I missing something? part should be treated the same way to include the alpha dependence right? Or am I missing something?BTW, also thanks for showing me the [math] tag! Really useful! |
| All times are GMT -4. The time now is 19:41. |