 |
|
|
[Sponsors] | |||||
fvc::laplacian(rAUf, p_rgh) versus fvm::laplacian(rAUf, p_rgh) |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Dear all,
I have a problem to understand the way how OpenFoam dicretizes the pressure equation. There is already a lot of information on this forum, but always on the explicit formulation. E.g. Code:
fvc::laplacian(rAUf, p_rgh) Code:
fvc::surfaceIntegrate(rAUf*fvc::snGrad(p_rgh)*mag(mesh.Sf())) Also Code:
fvc::surfaceIntegrate(rAUf*fvc::snGrad(p_rgh)*mag(mesh.Sf())-phiHbyA) Code:
fvc::laplacian(rAUf, p_rgh) - fvc::div(phiHbyA) But if I use fvScalarMatrix p_rghEqn ( fvm::laplacian(rAUf, p_rgh) == fvc::div(phiHbyA) ); the equation is decitized into a linear matrix equation type Code:
S - A * p_rgh = rA Is there any explanation to this? Regards, Daniel |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
I think I have an idea where this may come from. OpenFoam uses a feature called "non-othogonal correction". It supposely takes care of this issue. In order to see, if it is doing what I need, I can add non-orthogonal corrector loops and hope this does change something.
It would be nice to have some measurement of effictiveness of non-othogonal correction. I would need the residuals of the matrix iteration and, divide them by the expicit error (div (phi) in this case and some the absolute of these local errors up, eventually divide it by the number of cells. This would give me some measure if the non-orthogonal correction does something. Is there some method to get the matrix residuals. I do not see any of such object in the solverperformance declaration. Regards, Daniel |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
I checked the non orthogonal correction. Even this swithed off, I get the same inconsistency. So, I am kind of stuck here. Is there anybody who has an explanation? some higher order terms, which are neglegted in fvm discretization procedure?
Curreously: if I set use the explicit error and add it to a 2nd fvm discretization, the deviation remains. I am kind of stuck here. Is there somebody who has an idea? Regards, Daniel |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Jan
Join Date: Oct 2014
Posts: 8
Rep Power: 11  |
Hey danny,
I'm very new here and as you will have recognized I myself am also a little bit lost  To be honest I don't really see what your question is ... As I understand it, you want to know what the difference between the explicit and the implicit class is. I am not sure if I got it right myself ... I am asking myself the same thing for some time now  but as the "Programmers Guide" says: "vm and fvc contain static functions, representing differential operators, e.g. ∇ 2 , ∇ • and ∂/∂t, that discretise geometricField < Type > s. The purpose of defining these functions within two classes, fvm and fvc, rather than one, is to distinguish: • functions of fvm that calculate implicit derivatives of and return an fvMatrix < Type > • some functions of fvc that calculate explicit derivatives and other explicit calcula- tions, returning a geometricField < Type > ." (P-36) So I think the main difference is that derivatives are calculated in different ways. (see http://www.sosmath.com/calculus/diff/der05/der05.html ) Since the path to your solution is a different one this may (or will) cause a small difference in the numerical solution. Though there is a small difference both solutions should be pretty similar and about equally "correct" (and roughly equally wrong) I don't know much about the "non-orthogonal correction" loops but they seem to be important in some cases ... I didn't really get what they do yet ... (P-51) Sorry - I know I'm not very helpful here ... but as I mentioned I'm not even sure what exactly your problem is ... and I don't know how you can sum up exact differences ... |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
It is getting even more confusing since I added a comment line in the gausslapacianscheme and it is not to be found in the output. I think I have to sleep this over.
Since CFD uses linear discretization exclusively, You can always represent a differential equation as A * x = b, A being a matrix, x the value vector and b the source term. So, there should not be no difference to the explicit calculation unless there is some multiplication. E.g. in the convective term there is a quadratic term (rho phi U), but this is treated is a linear relationship too, since only U is treated implicetly. By the way, fvm::lapalcian(A) does exists already in the namespace. It is treated the same way I told you, but consideres non-othogonal correction. You can switch it off though. Regards, Daniel |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
I put info statements into laplacianScheme.C. It compiles, but there is no output. Is there any reason to this? Or do I look into the wrong file? To test, I simply did this:
Code:
// if (fv::debug)
{
Info<< "laplacianScheme<Type, GType>::New(const fvMesh&, Istream&) : "
"constructing laplacianScheme<Type, GType>"
<< endl;
}
In the application solver, I call Code:
fvScalarMatrix pcorrEqn
(
fvm::laplacian(rAUf, pcorr) == fvc::div(phiHbyA)
);
Is there anybody who has an idea? The same happens, if I add info statements into gaussLaplacianScheme.C Regards, Daniel |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello,
Now it becomes more and more tricky. I have 2 implicit laplacians in my code, one explicit laplacian. So far, so simple. I put info statement into the code. It seems that Code:
template<class Type, class GType> tmp<fvMatrix<Type> > laplacianScheme<Type, GType>::fvmLaplacian  . .When the individual laplacians are built, Code:
template<class Type, class GType> tmp<fvMatrix<Type> > gaussLaplacianScheme<Type, GType>::fvmLaplacianUncorrected  . . The explicit laplacian call also does not get called by the pcorrEq.flux() command. Is there anybody who knows how the laplacian call logic works? It would be nice to have that of the snGrad logic too, since the explicit laplacian calls snGrade (even though maybe not, since the fvc laplacian does not get called). Regards, Daniel |
|
|
|

|
|
|
|
|
#8 | |||
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,974
Blog Entries: 45
Rep Power: 128       |
Greetings to all!
@Daniel: Sorry, but only today did I manage to look into this and I have to say that I'm only able to answer questions regarding code itself, I don't know enough how OpenFOAM discretizes the equations  Quote:
Quote:
Quote:
Code:
if (this->tsnGradScheme_().corrected())
{
tfaceFluxCorrection() +=
SfGammaSn*this->tsnGradScheme_().correction(vf);
}
If you're trying to find your bearings in the source code, hopefully this description will put you in the right direction. Best regards, Bruno
__________________
|
||||
|
|

|
||||
|
|
|
#9 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Thanks Bruno,
This is very helpful. Only a little question, rebuilding the solver, you mean the application solver (interFoam bla. bla.) or the matrix solver, meaning rebuilding within src/OpenFOAM? Regards, Daniel |
|
|
|

|
|
|
|
|
#10 | |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,974
Blog Entries: 45
Rep Power: 128       |
Hi Daniel,
I think you're referring to this paragraph: Quote:
Best regards, Bruno |
||
|
|

|
||
|
|
|
#11 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello Bruno,
Well, I did what you said, but there is no difference. My application solver is located in run/myworks, it is home build one based on interDymFoam. Maybe this makes a difference... It should not though. I also tried wclean upfront of wmake, nothing different though. Reading the code, I thought the laplacian is structured the following way: fvm: the header files are located in laplacianScheme.H, which then calls laplacianScheme.C for the definitions. There are a number of different definitions, basically depending whether Gamma is present or if Gamma is not (otherwise Gamma is defined as unity), and whether Gamma is taken at cell center, so a face interpolation is needed. They all converge into a face interpolated Gamma laplacian. This then should call (somehow?) Code:
template<class Type, class GType> tmp<fvMatrix<Type> > gaussLaplacianScheme<Type, GType>::fvmLaplacian After solving the flux function is called directly on the matrix equation, as you correctly pointed out. This is where I suspect a mistake in the code, but regardless, I need to be sure that the way how it is described here is correct. Adding a comment line in either fvmLaplacian or gammaSnGradCorr does not show up, in fvmLaplacianUncorrected it does. They all are template classes. fvc: very much the same way, only there is no matrix built, but simply the div operator is used and snGrade to determine the face fluxes. Curiously, this operator does not get called at all. I obviously put an fvc::Laplacian into the application solver code. If you could help what else I could do, I would appreciate. I will try to compile directly in the native interFoam solver, just to see if the problem stems from there. Regards, Daniel |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
So, now I compiled interFoam new and ran the application. I attach the 2 modified laplacian files, where I put comment lines in.
The output is: HTML Code:
... fvmLaplacian is here 3... fvmLaplacian is here 1 fvmLaplacian is here 3 fvmLaplacian is here 3... fvmLaplacian is here 1 fvmLaplacian is here 3 fvmLaplacian is here 3... etc. In my opinion, looking into the code, for each "fvmLaplacian is here 3" mentioned above, the output should be: HTML Code:
fvmLaplacian is here 5 tgammaSnGradCorr is here fvmLaplacian is here 3 HTML Code:
fvcLaplacian is here 4 HTML Code:
fvcLaplacian is here 2 Looking back into the code, it is striking that only fvmLaplacianUncorrected shows up within gaussLaplacianScheme. C. If one looks into the header file, this is the only static template (code in gaussLaplacianScheme.H). Moreover, at the bottom there is following code Code:
// Use macros to emulate partial-specialisation of the the Laplacian functions
// for scalar diffusivity gamma
#define defineFvmLaplacianScalarGamma(Type) \
\
template<> \
tmp<fvMatrix<Type> > gaussLaplacianScheme<Type, scalar>::fvmLaplacian \
( \
const GeometricField<scalar, fvsPatchField, surfaceMesh>&, \
const GeometricField<Type, fvPatchField, volMesh>& \
); \
\
template<> \
tmp<GeometricField<Type, fvPatchField, volMesh> > \
gaussLaplacianScheme<Type, scalar>::fvcLaplacian \
( \
const GeometricField<scalar, fvsPatchField, surfaceMesh>&, \
const GeometricField<Type, fvPatchField, volMesh>& \
);
Regards, Daniel |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello Bruno and you other alls,
I found the solution, it is a tricky one, not that obvious and, honestly, I do not understand the reason why it is implemented this way. Maybe, Bruno, can you shed some light on this? The fvmlaplacian as well as the fvclaplacian actually exists twice in the source code. The alternative code is located in gaussLaplacianSchemes.C. It is written after a #define statement, so everything is in pink and backslashes at the end of lines. It can be edited as any other code (and compiles too). The declaration line the the fvm laplacian used is Code:
template<> \ Foam::tmp<Foam::fvMatrix<Foam::Type> > \ Foam::fv::gaussLaplacianScheme<Foam::Type, Foam::scalar>::fvmLaplacian Code:
template<class Type, class GType> tmp<fvMatrix<Type> > gaussLaplacianScheme<Type, GType>::fvmLaplacian I now can figure out the difference where the difference in fvm and fvc comes from and will report, if succesful. Regards, Daniel |
|
|
|

|
|
|
|
|
#14 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,974
Blog Entries: 45
Rep Power: 128       |
Hi Daniel,
The file "gaussLaplacianSchemes.C" has dedicated specializations of the main template. This is a C++ feature, where we can define a main template structure and then have a specific implementation have a slightly different thing done in some situations. In this example, we have the main template class "gaussLaplacianScheme", with this template structure: Code:
template<class Type, class GType> class gaussLaplacianScheme Code:
tmp<GeometricField<Type, fvPatchField, volMesh> > fvcLaplacian
(
const GeometricField<Type, fvPatchField, volMesh>&
);
tmp<fvMatrix<Type> > fvmLaplacian
(
const GeometricField<GType, fvsPatchField, surfaceMesh>&,
const GeometricField<Type, fvPatchField, volMesh>&
);
tmp<GeometricField<Type, fvPatchField, volMesh> > fvcLaplacian
(
const GeometricField<GType, fvsPatchField, surfaceMesh>&,
const GeometricField<Type, fvPatchField, volMesh>&
);
Then in "gaussLaplacianSchemes.C" we have dedicated implementations for when "GType" is "scalar": Code:
template<> \
Foam::tmp<Foam::fvMatrix<Foam::Type> > \
Foam::fv::gaussLaplacianScheme<Foam::Type, Foam::scalar>::fvmLaplacian \
( \
const GeometricField<scalar, fvsPatchField, surfaceMesh>& gamma, \
const GeometricField<Type, fvPatchField, volMesh>& vf \
) \
...
template<> \
Foam::tmp<Foam::GeometricField<Foam::Type, Foam::fvPatchField, Foam::volMesh> >\
Foam::fv::gaussLaplacianScheme<Foam::Type, Foam::scalar>::fvcLaplacian \
( \
const GeometricField<scalar, fvsPatchField, surfaceMesh>& gamma, \
const GeometricField<Type, fvPatchField, volMesh>& vf \
) \
Comparing the source code, the idea is that the "gamma" field (generic name) that this specialization uses is something that is previously calculated... probably the "phi" field. While the generic template class has to always calculate the "gamma" field. Best regards, Bruno
__________________
|
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello Bruno,
This definetly helped me to understand the code. I found the missmatch, but I do not know the motivation of it. Basically the fvm::laplacian does a balance over the cell faces of the product of the gradient of some surface field and another surface field. That other surface field is called gamma, sometimes called diffusity. The gradient of the 1st surface field is derived from the cell values of the field. In order to do a correct balance, you need some kind of flow over a face. Then you sum them up over each faces over a cell (and apply boundary conditions). The result of that sum has the same unit as the individual face flows. For pcorr.Eq in interFoam this is m3/s. You now may divide each balance value by some norming factor. But this would mean that you cannot add or substract additional terms. So, my guess is that the implementation is correct. What is not correct is the explicit implementation. You can see this in fvcSurfaceIntegrate.C: Code:
template<class Type>
void surfaceIntegrate
(
Field<Type>& ivf,
const GeometricField<Type, fvsPatchField, surfaceMesh>& ssf
)
{
const fvMesh& mesh = ssf.mesh();
const labelUList& owner = mesh.owner();
const labelUList& neighbour = mesh.neighbour();
const Field<Type>& issf = ssf;
forAll(owner, facei)
{
ivf[owner[facei]] += issf[facei];
ivf[neighbour[facei]] -= issf[facei];
}
forAll(mesh.boundary(), patchi)
{
const labelUList& pFaceCells =
mesh.boundary()[patchi].faceCells();
const fvsPatchField<Type>& pssf = ssf.boundaryField()[patchi];
forAll(mesh.boundary()[patchi], facei)
{
ivf[pFaceCells[facei]] += pssf[facei];
}
}
ivf /= mesh.Vsc();
}
I tried it out and indeed fvc::div(phi) has the unit 1/s. I have not checked all the other implementations (fvm:div). Do you have an idea why the fvc::surfaceIntegrate is implemented such? Regards, Daniel |
|
|
|

|
|
|
|
|
#16 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,974
Blog Entries: 45
Rep Power: 128       |
Hi Daniel,
I won't be able to look into this in more detail any time soon, but I do suggest you check Hrvoje Jasak's PhD Thesis: http://powerlab.fsb.hr/ped/kturbo/Op...jeJasakPhD.pdf - hopefully this and other details are explained there. Best regards, Bruno |
|
|
|

|
|
|
|
|
#17 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello,
For those who are interested in this topic, this is what I figured out: First, and most importantly, the implementation is fundametally correct. On can debate on some minor points, see below. When you do a balance on a control volume, or as it is named in OpenFoam, a cell, you have to establish an equation that has the dimension flow. Basically, the property of the cells changes because something flows inside the cell or outside therefrom. This corresponds to the integral form of the Narvier Stakes Equation. As an example, take: 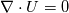 The integral form is: 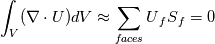 The unit of this equation is m^3/s. U^f is the volumetric face flux and the product of face surface and flux is the volumetric face flow phi. fvm operators and fvc both need to have the same dimension, in this case m^3/s. What is confusing is, that the for fvc::div, you get the dimension 1/s, since the result of the balance is divided by the cell volume. I can only guess why this is done so, maybe it is a convention or whatever (since nabla dot U also is of dimension 1/s). Now, if one adds a fvc::div term to the balance equation, the result is automatically remultiplied by the cell volume. So, you divide by the cell volume and remultiply and get back to the same result. If you look at the code in your application solver, the same code line fvc::div within a balance equation (matrix equation) and as regular calculation have different results. This is what did confuse me. Some other points: - I found small deviations because of the numerical precision since multiplying and redividing by a number does not lead to identical results. These errors are very small, but can be annoying. - the non-orthogonal correction has been removed from the snGrad and therefore does not apply for the explicit laplacian. This term should be present in the snGradScheme.C. - if non orthogonal correction is to be used, you need to add "Gauss linear uncorrected" for the laplacianSchemes in fvSchemes.C to apply the corretor for the fvm::div operator as well for the flux correction, and "corrected" for the snGradSchemes to apply for the fvc::div operator. Note that there is a fvc::div embedded in the fvm::div operator (the non orthogonal correction), so you get some kind of "correction of the correction". Note also that the correction will apply for all "stand alone" snGrad operators. I do not know the thinking behind this is since what needs to be corrected is the gradient and not the divergence operator. So, if you want gradient correction, lapalcians always need to be corrected too since the gradient is an integral part of the laplacian. Hope these explanations help. Any comment is welcome. Regards, Daniel |
|
|
|

|
|
|
|
|
#18 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,974
Blog Entries: 45
Rep Power: 128       |
Hi Daniel,
Many thanks for the detailed explanation! About your questions regarding how the correctors were implemented, have you read Hrvoje Jasak's PhD thesis "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows"? It has a lot of these kinds of details explained in there. I've only managed to do a very quick search right now... and I ended up getting lost  Nonetheless, subsections 1.2 and 3.5 seem to be relevant to your questions. Nonetheless, subsections 1.2 and 3.5 seem to be relevant to your questions.edit: Helpful thesis links here: http://openfoamwiki.net/index.php/IcoFoam Best regards, Bruno Last edited by wyldckat; September 19, 2015 at 12:22. Reason: see "edit:" |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello Bruno,
Yes, I read this thesis, at least the relevant parts that you mention. They are very helpful in understanding the code. Unfortunatly, the code that is currently implemented is slightly different than the original "over relaxed" method. You can switch to other non orthogonal correction methods by changing the comment "/" sign location in surfaceInterpolation.C. There is one relevant equation that hit me, which is eq. 3.138. The author forgot to put the integral sign over volume on the left hand side of the equation, So, left hand side you get unit 1/s and right hand side m^3/s... It is also important to understand why the balance is not done on a reduced by cell volume basis. The matrix in pEq would not be symmetric anymore, increasing computional cost for solving that matrix equation. This being said, I still not understand why there is this double coding of the laplacian operator. The code in gaussLaplacianSchemes.C covers both scalar fields as vector scalar fields. Regards, Daniel |
|
|
|

|
|
|
|
|
#20 | ||||
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,974
Blog Entries: 45
Rep Power: 128       |
Hi Daniel,
Quote:
 If we compare with the definition in equation 3.15, the missing term on the left side is "Vp", which is the cell volume, which would fix the problem with the units. Since it's equal to zero either way, it's possible that this was the reason the typo wasn't spotted sooner. Quote:
 What do you mean by the following expression? What do you mean by the following expression?Quote:
Quote:
Best regards, Bruno |
|||||
|
|

|
|||||
 |
| Tags |
| laplacian operator |
| Thread Tools | Search this Thread |
| Display Modes | |
|
|