surface gradient
 

Hi,

in the openFoam programmer's guide on P-40 there is an explanation for the
surface normal gradient:

surfaceScalarField gradnq=fvc::snGrad(q);

which gives (grad(q))_f*n_f.

I want to calculate only grad(q)_f , it should be something like:

surfaceVectorField gradq=????????(q);

Maybe someone has an useful idea,
thanks, M.

Hi Martin,

Isn't that simply fvc::grad()? Or am I missing the point of your question?

Hi Gijs,


Thanks for your reply, fvc::grad is using the Gauss integral theory to calculate the gradient at the cell center – so it's not what I was seeking for.



As I can see now, the gradient at the face center will not be calculated within the snGrad calculation. The surface normal Gradient (for an orthogonal mesh) will be calculated directly by

g[faceI]=(v[neighbour[faceI]]-v[owner[faceI]])/d


(This can be seen in src/finiteVolume/finiteVolume/snGradSchemes/snGradScheme.C on line 142.)


The calculation applies to internal Faces.


For fully understanding I would like to know how the snGrad is calculated on boundary Faces.


Maybe you (or someone else) can tell me where I can find the calculation for snGrad on the boundary faces.


Thanks,
Martin.

Hi Martin,

Right, I see :). I am not entirely sure, but from the discussion here I gather that $WM_PROJECT_DIR/applications/utilities/postProcessing/wall/wallGradU.C contains some hints. In particular, this might be interesting:

Hi Gijs,

I think in your example snGrad() will also be used as a member function of the boundary field (patchfield). I think I have found the calculation in

src/finiteVolume/fields/fvPatchFields/fvPatchField/fvPatchField.C in line 180:


// Return gradient at boundary
template<class Type>
Foam::tmp<Foam::Field<Type> > Foam::fvPatchField<Type>::snGrad() const
{
return (*this - patchInternalField())*patch_.deltaCoeffs();
}


Now I will try to find out if there is a non-orthogonal mesh correction of the surface normal gradient on the boundary.

M.

Hi, I have a simple question.

I have volScalarField .
I calculate fvc::grad(alpha1).
This mean, im simplest case, i do:
(1)
fvc::grad(alpha)
or (2)
fvc::grad(alpha) ?
(1) or (2) is the right one?

And
fvc::snGrad
this is centr. diff. approx., or?

Greetings, Alicja

Hi Alicja,

This is, in most cases, the right one (although it's sum_f Sf alpha_f. I say "most cases", because it can change a bit with the difference scheme used. What fvc::grad in the case above does, is use the values for alpha interpolated on the faces (alpha_f), multiply it with the relevant face vector (which is proportional to the face area), and then sum all of that up over the selection of faces (usually all, but not necessarily).

In a way yes, but normally used for boundary faces, snGrad is the surface normal gradient. Another important difference is that grad() is a vector field, while sngrad() is not ...

Hi Gijs!

Thx for your Answer!

I have a further question about fvc:: (alpha). I use the most simple discretisation scheme, 'Gauss linear'.

I took a look at interFoam solver.
I want to know, how is the curvature calculated.
I have this to discretise: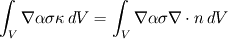

See interfaceProperties.C
To calculate :
firstly i calculate fvc::grad(alpha).
So i 've run debug modus and i was in this class,
gaussGrad.C
firstly at line 134 and then at line 55. You see at the line 113 multiplikation with .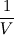
Which term is the correct one, (1) or (2)?

(1)
fvc::grad(alpha) http://www.cfd-online.com/Forums/vbL...e3de52d3-1.gif
or (2)
fvc::grad(alpha) http://www.cfd-online.com/Forums/vbL...0d74d68e-1.gif ?

I think the term (1) is the correct one. Perhaps later when i build the matrix or equation system i do multiply with .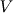
See fvMatrix.C at the line 1448. But i'm not sure.

Greetings, Alicja

Hello
the first one is true but not with dot product(.) . because it's for divergence not grad.

snGradient
 

hi
i need the formulation of crrected snGradien scheme for laplacian(Q)
can help me?