 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Qingang Xiong
Join Date: May 2012
Location: Ames, IA, USA
Posts: 20
Rep Power: 13  |
Dear members,
I am incorporating KTGF for sovling the alphaEqn.H in twoPhaseEulerFoam. In this sovler, is the "ppMagf" to be differentiated alpha to particle granular temperature? If so, I think it is so complex. Looking forward to your reply. Thank you! |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Alberto Passalacqua
Join Date: Mar 2009
Location: Ames, Iowa, United States
Posts: 1,912
Rep Power: 36   |
Quote:
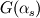 . You should check the definition of this term in the relevant literature, to have some background on the model. If you consider a granular phase, with equation of state: . You should check the definition of this term in the relevant literature, to have some background on the model. If you consider a granular phase, with equation of state: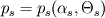 , ,the normal stress modulus is 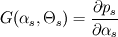 In twoPhaseEulerFoam ppMagf = 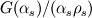 , due to the treatment used in discretizing the phase momentum equation. , due to the treatment used in discretizing the phase momentum equation.Best,
__________________
Alberto Passalacqua GeekoCFD - A free distribution based on openSUSE 64 bit with CFD tools, including OpenFOAM. Available as in both physical and virtual formats (current status: http://albertopassalacqua.com/?p=1541) OpenQBMM - An open-source implementation of quadrature-based moment methods. To obtain more accurate answers, please specify the version of OpenFOAM you are using. 
Last edited by alberto; May 8, 2012 at 12:50. Reason: Re-wrote equations in LaTeX |
||
|
|

|
||
|
|
|
#3 | |
|
New Member
Qingang Xiong
Join Date: May 2012
Location: Ames, IA, USA
Posts: 20
Rep Power: 13  |
Quote:
Thank you very much for your reply. So from your description, Theta_s can be regarded as an independent variable to alpha_s though Theta_s is implicitly obtained from alpha_s. Am I right? |
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Alberto Passalacqua
Join Date: Mar 2009
Location: Ames, Iowa, United States
Posts: 1,912
Rep Power: 36   |
Quote:
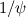 , being , being 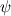 the compressibility of the particle phase, which is defined as the compressibility of the particle phase, which is defined as 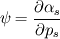 This is analogous to the case of an ideal gas, where you have 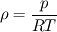 so 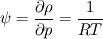 The difference is that, in a granular flow, generally 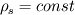 , and the compressibility is due to changes in the phase fraction , and the compressibility is due to changes in the phase fraction 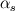 . .Best,
__________________
Alberto Passalacqua GeekoCFD - A free distribution based on openSUSE 64 bit with CFD tools, including OpenFOAM. Available as in both physical and virtual formats (current status: http://albertopassalacqua.com/?p=1541) OpenQBMM - An open-source implementation of quadrature-based moment methods. To obtain more accurate answers, please specify the version of OpenFOAM you are using. 
Last edited by alberto; May 8, 2012 at 12:46. Reason: Corrected and re-wrote equations with LaTeX |
||
|
|

|
||
|
|
|
#5 |
|
New Member
Qingang Xiong
Join Date: May 2012
Location: Ames, IA, USA
Posts: 20
Rep Power: 13  |
Quote:
I understand what you mean. This point is clear to me. Thank you veru much! Best |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure instabilities with interDyMFoam for the floatingObject case | nbadano | OpenFOAM Running, Solving & CFD | 15 | October 15, 2021 06:35 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 06:27 |
| Using pressure outlet BC | Shreyansh | FLUENT | 0 | November 5, 2010 14:57 |
| Help ASAP! pressure inlet & outlet | engahmed | FLUENT | 0 | June 13, 2010 15:33 |
| Setting pressure and velocity in inlet | Asghari | FLUENT | 5 | September 22, 2006 13:23 |