 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Oliver Borm
Join Date: Mar 2009
Posts: 60
Rep Power: 17  |
Hello,
I've derived the momentum equation for the relative frame of reference formulated with the absolute velocity here. The result  is coincident with the literature but not with the formulation in the fluent manual. The second term on the left hand side is different, whereas the rest is equal. It can be shown that the tensor 2. rank from the dyadic product of (vec{c} \otimes vec{w}) is not symmetric, if you write it down component-by-component in cartesian coordinates, you will see that (vec{c} \otimes vec{w} \neq vec{w} \otimes vec{c}). So there seems to be a bug in the fluent manual. That's why I think, the formulation of the UEqn in the MRFSimpleFoam solver is also not valid. There is fvm::div(phi, U), in this case phi denotes to w_i (relative velocity) for each spatial direction. Am I right? |
|
|
|

|
|
|
|
|
#2 |
|
Member
Oliver Borm
Join Date: Mar 2009
Posts: 60
Rep Power: 17  |
There are two different derivations of Navier-Stokes equations for so called "Multiple Reference Frames" (MRF) or "Multiple Frames of Reference" (MFR):
If anybody wants to use the actual implementation of the MRF library within a transient solver (that includes all compressible transsonic solvers), one has to be certain, that the local time derivation is calculated with the relative velocity ( 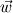 ) and not with the absolute velocity ( ) and not with the absolute velocity (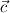 ) ! As this could be a little bit tricky, I would prefer either the second notation of the MRF or using the formulation with the relative velocity in the relative frame of reference, as this is done in the SRF library, with an appropriate rotor-stator interface. ) ! As this could be a little bit tricky, I would prefer either the second notation of the MRF or using the formulation with the relative velocity in the relative frame of reference, as this is done in the SRF library, with an appropriate rotor-stator interface.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Theoretical analysis and modelling of gas-solids | Langa Ntetye | Main CFD Forum | 0 | December 13, 2007 06:10 |
| a simple theoretical doubt | Rahul | FLUENT | 1 | May 10, 2007 17:28 |
| theoretical equations | wilson | CFX | 3 | March 4, 2005 08:46 |
| Discussion forums on Theoretical FD? | Nomad | Main CFD Forum | 4 | March 16, 2004 12:58 |
| Fluent Online Theoretical Reference | Danial | FLUENT | 2 | September 23, 2001 15:29 |