 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Aug 2011
Posts: 6
Rep Power: 14  |
Hello,
I am trying to solve a type of heat equation: 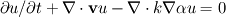 The difference to the standard heat equation is the scalar field alpha. The problem is that the last term cannot be expressed as fvm::laplacian(k,alpha*u), because apparently alpha*u is not the right class for this argument, and the compiler fails. How can this PDE be solved? Thanks Gunnar Last edited by gunnar2; August 8, 2011 at 13:26. Reason: correction: replaced [math]\nabla\cdot\phi u[/math] with [math]\nabla\cdot\mathbf{v} u[/math] |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
ata kamyabi
Join Date: Aug 2009
Location: Kerman
Posts: 323
Rep Power: 17  |
Hi
I think you can define a new field newfield=alpha*u and use fvc::laplacian(k,new) good luck |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Aug 2011
Posts: 6
Rep Power: 14  |
But I need the implicit (fvm::laplacian), not the explicit (fvc::laplacian) term.
If there is no such term, it should be possible to use something like fvm::laplacian(k,u)*diag(alpha) for 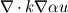 . .diag(alpha) would be a sparse diagonal matrix with the entries of the field alpha on it's diagonal, but I don't think such matrix exists in Openfoam. What do you think, does it make sense to implement it? Thanks Gunnar |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
ata kamyabi
Join Date: Aug 2009
Location: Kerman
Posts: 323
Rep Power: 17  |
Hi
I do not know 
|
|
|
|

|
|
|
|
|
#5 |
|
Member
Michael Roth
Join Date: Mar 2009
Location: Guelph, Ontario, Canada
Posts: 50
Rep Power: 17  |
How about a little chain rule? i.e. split into:
Code:
\nabla \cdot ( k \alpha \nabla u ) + \nabla \cdot ( k u \nabla \alpha ) |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
ata kamyabi
Join Date: Aug 2009
Location: Kerman
Posts: 323
Rep Power: 17  |
Hi
But you loose conservative form. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Santiago Marquez Damian
Join Date: Aug 2009
Location: Santa Fe, Santa Fe, Argentina
Posts: 452
Rep Power: 23  |
First of all the equation appears to be not consistent, the first and last terms are vectorial, meanwhile the second one is scalar.
Regards.
__________________
Santiago MÁRQUEZ DAMIÁN, Ph.D. Research Scientist Research Center for Computational Methods (CIMEC) - CONICET/UNL Tel: 54-342-4511594 Int. 7032 Colectora Ruta Nac. 168 / Paraje El Pozo (3000) Santa Fe - Argentina. http://www.cimec.org.ar |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Mieszko Młody
Join Date: Mar 2009
Location: POLAND, USA
Posts: 145
Rep Power: 17  |
Hi Gunnar,
If the only think you need is modification of the discretization matrix (by multiplying diag(alpha)), then you can change the matrix itself. See the PISO algorithm from icoFoam: http://openfoamwiki.net/index.php/IcoFoam You can do similar and: 1. discretize alpha 2. UEqn.A() = UEqn.A()*alpha_discretized maybe will work... ZMM |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Mieszko Młody
Join Date: Mar 2009
Location: POLAND, USA
Posts: 145
Rep Power: 17  |
Hi Kai,
Of course, I would proceed using this transformation. Currently I have some issues with laplacian operator in OFoam as well. Could you see my post: http://www.cfd-online.com/Forums/ope...n-problem.html Maybe you will have some suggestions... Thanks ZMM |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Modifying the laplacian operator | mlawson | OpenFOAM Running, Solving & CFD | 22 | July 16, 2018 04:56 |
| [Other] Modify mesh runtime | Daniele111 | OpenFOAM Meshing & Mesh Conversion | 8 | December 19, 2010 15:43 |
| "=" or "==" when I modify BC (fixedGradient) during run ? | Cyp | OpenFOAM Programming & Development | 0 | December 14, 2010 08:12 |
| Crank Nicholson scheme for Laplacian failed | Cyp | OpenFOAM | 3 | July 19, 2010 07:58 |
| fluent add additional zones for the mesh file | SSL | FLUENT | 2 | January 26, 2008 11:55 |