 |
|
|
[Sponsors] | |||||
Incompressible turbulence models: strange implementations? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Alessandro
Join Date: May 2009
Location: Genova
Posts: 47
Rep Power: 16  |
Hi FOAMers!
I'm doing some programming works on k-Omega SST alternative forms in OF and I found some strange implementations in the incompressible versions of turbulence models. In particular I'm wondering if the formula for the Reynolds stress tensor R, the deviatoric part of the effective stress tensor devReff and its divergence divDevReff are correct. To my knowledge, the formulas for all of these quantities are the same for compressible and incompressible fluids, being the latter a particular case of the first (with the assumption that div(U_i) = tr(S_ij) = 0 , being S_ij = 1/2(d u_i/d x_j + d u_j/d x_i) the symmetric part of the grad U_i tensor, a.k.a the strain rate tensor). Anyway the formulas in OF for the incompressible models seems a little puzzling because: 1. Reynolds stress tensor : R_ij = 2/3 I_ij k - nut (2 S_ij - 2/3 div U_i I_ij) in which for the incompressible case the last term drops. The OF formulation is: R = ((2.0/3.0)*I)*k_ - nut_*twoSymm(fvc::grad(U_)) where 2/3 div U_i I_ij has been dropped. 2. Deviatoric part of the effective stress tensor : D_ij = nuEff (2/3 div U_i I_ij - 2 S_ij) in which for the incompressible case the first term drops. The OF formulation is: devReff = - nuEff()*dev(twoSymm(fvc::grad(U_))) where the divergence term has NOT been dropped, because of the dev operator. 3. Divergence of the deviatoric part of the effective stress tensor : div(D_ij) = 2/3 d/d x_i( nuEff d U_k/d x_k ) - 2 d/d x_j( nuEff S_ij ) = 2/3 d/d x_i( nuEff d U_k/d x_k ) - d/d x_j( nuEff d U_i/d x_j + nuEff dU_j/d x_i ) in which for the incompressible case the first term drops. The OF formulation is: divDevReff = - fvm::laplacian(nuEff, U) - fvc::div(nuEff()*dev(fvc::grad(U)().T())) where the divergence term has NOT been dropped, because of the dev operator. Moreover it has been erroneously included as 1/3 div U_i , not as 2/3 div U_i I_ij, because operator dev is used instead of dev2 and there isn't any twoSymm in the argument, as for D_ij above! From the point of view of strict numerics this shouldn't have any impact on the solution, because for incompressible fluids div U_i = 0. Anyway for the mathematics this is not correct. Maybe if div U_j is not near machine zero, could this cause an error? I'd like to know your opinions and in particular I'd like to know: - Are there reasons for not keeping the divergence term in Reynolds stress tensor, but keeping it in the effective stress tensor? - Can anybody explain me why there is dev in the divergence of the deviatoric part of the stress tensor instead of dev2 operator? Thanks and let's wait for some answers!  Alex. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Timofey Mukha
Join Date: Mar 2012
Location: Stockholm, Sweden
Posts: 118
Rep Power: 14  |
Indeed, I would like to have this explained as well.
To basically reiterate the original post : under the Stokes assumption of zero bulk viscosity we have the viscous stress tensor divided by the density as 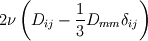 In incompressible flow the last term is zero due to continuity yet the implementation is Code:
//src/turbulenceModels/incompressible/LES/GenEddyVisc/GenEddyVisc.C
tmp<volSymmTensorField> GenEddyVisc::devReff() const
{
return -nuEff()*dev(twoSymm(fvc::grad(U())));
}
By expanding 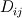 we get we get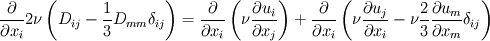 So we have the laplacian term plus the divergence of the transposed velocity gradient minus double the trace. But in the implementation we have Code:
//src/turbulenceModels/incompressible/LES/GenEddyVisc/GenEddyVisc.C
tmp<fvVectorMatrix> GenEddyVisc::divDevReff(volVectorField& U) const
{
return
(
- fvm::laplacian(nuEff(), U)
- fvc::div(nuEff()*dev(T(fvc::grad(U))))
);
}
So the question is, why is dev used in the first place since the trace is zero anyway. Formalism? And if so, why is there a 2 missing in the divDevReff? |
|
|
|

|
|
|
|
|
#3 |
|
Member
Alessandro
Join Date: May 2009
Location: Genova
Posts: 47
Rep Power: 16  |
Hello tian,
Just have a look at this post by Henry. Here is my personal view of it: ![\frac{\partial}{\partial x_j} \left[ 2 \nu_e \frac{1}{2} \left( \frac{\partial u_i^{n+1}}{\partial x_j} + \frac{\partial u_j^{n}}{\partial x_i} \right) - \frac{2}{3} \nu_e \frac{1}{2} \left( \frac{\partial u_k^{n+1}}{\partial x_k} + \frac{\partial u_k^{n}}{\partial x_k} \right) \delta_{ij} \right] \frac{\partial}{\partial x_j} \left[ 2 \nu_e \frac{1}{2} \left( \frac{\partial u_i^{n+1}}{\partial x_j} + \frac{\partial u_j^{n}}{\partial x_i} \right) - \frac{2}{3} \nu_e \frac{1}{2} \left( \frac{\partial u_k^{n+1}}{\partial x_k} + \frac{\partial u_k^{n}}{\partial x_k} \right) \delta_{ij} \right]](/Forums/vbLatex/img/5f745a52d9b9d28733e908c61cabe788-1.gif)  which can be sorted into: 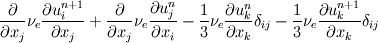 where the first term is the implicit (compact) laplacian and the second term is the explicit (extended) div grad. The third term accounts for the non div-free velocity field (it's a projection method) and the fourth term can be considered lumped into implicit pressure gradient. This will probably generate some a priori control on divergence of the momentum predictor velocity, certainly beneficial for the projection step which follows. Have a look at the literature, especially that about spectral and finite elements. Loosely speaking - if all of this seems too involved - it is a trick to keep the implicit part compact and to account for the divergence of the velocity predictor. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Timofey Mukha
Join Date: Mar 2012
Location: Stockholm, Sweden
Posts: 118
Rep Power: 14  |
Interesting, thank you!
|
|
|
|

|
|
 |
| Tags |
| dev, dev2, devreff, divdevreff, incompressible |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| KOmega Turbulence model from wwwopenFOAMWikinet | philippose | OpenFOAM Running, Solving & CFD | 30 | August 4, 2010 10:26 |
| Wall functions and turbulence models implementations | jposunz | OpenFOAM Running, Solving & CFD | 2 | October 23, 2009 04:02 |
| LES & DES turbulence models | Seva Reehal | CFX | 5 | October 18, 2009 08:44 |
| Tutorial 21: Turbulence models | spatialtime | CFX | 4 | April 24, 2009 05:25 |
| Turbulence models for GCV method dosen't work! | Sima Baheri | Phoenics | 0 | January 6, 2007 04:08 |