
 |
A few simple questions about linearUpwind and limitedLinear
I am a writing about the schemes that I used in my simulations in my thesis and could use some clarification on the linearUpwind and limitedLinear schemes. I have read http://www.cfd-online.com/Forums/ope...r-schemes.html and Alberto did a good explanation, but I need a little more clarification.
linearUpwind: I know linearUpwind is second order and bounded by a limiter (e.g. cellMDLimited from http://www.cfd-online.com/Forums/ope...lllimited.html). This is different than the limiters used in limitedLinear. In Fluent documentation, the definition of second order upwind is given as: 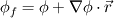 where 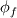 and and  are the face value of phi and the cell centered values of phi in the upstream cells respectively. I am reading through the code of linearUpwind and I see: are the face value of phi and the cell centered values of phi in the upstream cells respectively. I am reading through the code of linearUpwind and I see:Code:
GeometricField<Type, fvsPatchField, surfaceMesh>& sfCorr = tsfCorr();When is the sfCorr used to correct the value of the face? I guess I am just interested in generating a discussion and confirming or clarifying my thoughts. limitedLinear This again is second order and is bounded using a sweby limiter (http://www.cfd-online.com/Forums/ope...r-schemes.html post 16). I am just a little fuzzy on what the final simplified form of the equation is for limitedLinear (I admit I haven't looked at it as much as linearUpwind). I am out of my office and will look through Richard Pletcher, John Tannehill and Dale Anderson when I get a chance. Laslty, correct me if I'm wrong but the parameter following a definition of a limitedLinear declaration is passed to the limiter, where 1 uses the limiter and 0 does not (with anything in between being a blend). Sorry for the massive post, and any clarification would be fantastic and if I find an answer, I will post the result here. And for those interested on how I did the math in the forum, look at (http://www.cfd-online.com/Forums/sit...ne-forums.html) Dan |
on the limitedLinear, it seems that my knowledge of limiters is lacking and it may turn out to be a simple answer. Looking in Dr. Jasak's thesis (pg 98), I found that:
![\phi_f = (\phi_f)_{UD} + \Psi(r)\left[(\phi_f)_{HO}-(\phi_f)_{UD}\right] \phi_f = (\phi_f)_{UD} + \Psi(r)\left[(\phi_f)_{HO}-(\phi_f)_{UD}\right]](/Forums/vbLatex/img/736f57e6b0e22db22914c69474c71169-1.gif) where 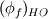 is the value of phi at the face for a higher order scheme. For limitedLinear, it is just the central difference scheme as the "HO" and the limiter ( is the value of phi at the face for a higher order scheme. For limitedLinear, it is just the central difference scheme as the "HO" and the limiter (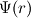 ) is a Sweby limiter (http://www.cfd-online.com/Forums/ope...ar-scheme.html). if there is more to add here or there are corrections then please do. ) is a Sweby limiter (http://www.cfd-online.com/Forums/ope...ar-scheme.html). if there is more to add here or there are corrections then please do.Dan |
Yes you are right. limitedLinear is using the Sweby limiter [1]. If you want further information about TVD Schemes and different limiters, I think [2] might be interesting to get a first brief impression.
About linearUpwind I don't know much. Till now I just thought it is something like linear upwind differencing but reading your post seems like its only half the story. [1] P.K. Sweby. High resolution schemes using flux limiters for hyperbolic conservation laws.SIAM Journal on Numerical Analysis, (Vol. 21):pp. 995–1011, 1984. [2] H. K. Versteeg and W. Malalasekera. An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson, 2007. |
@caramelo : I found a mistake in my first post concerning the linearUpwind definition and just corrected it (sorry about that). I did have a chance to look at the Sweby paper and also a few other sources on TVD schemes, very interesting. Thanks for the sources.
I see throughout the forum that the linearUpwind is bounded, but Ferziger and Peric' note that second order upwind is unbounded. My question is that if one uses Gauss linear as a grad scheme for linearUpwind, will this approach the traditional second order upwind and therefore unbounded? Also, is Gauss linear just the arithmetic average of the two cells or is it the distance weighted average similar to the linear divScheme for advection? Lastly, is the linearUpwind scheme only bounded if limited versions of the gradient scheme are used, i.e. limited linear, cellLimited, faceMDLimited etc.? Dan |
[Solved] A few simple questions about linearUpwind and limitedLinear
Quote:
Quote:
In the end I think that I have the answer that I was looking for. Dan |
Hi Dan,
Quote:
Apart from this, as far as I understand, linearUpwind scheme is unbounded as long as you don't specify one of the limiters cellLimited, faceLimited etc. Best, Florian |
Quote:
and of course: Quote:
Dan |
How can you find out which file contains the source code implementing the 'linearUpwi
Quote:
|
Linux commands to search for file names and within files are your friend. To look for the linearUpwind source, try
Code:
cd $FOAM_SRCCode:
cd $FOAM_SRC |
Thank you very much.
|
Quote:
I found your post which is very interesting for me. Could you please tell me how one can derive the equation above? I found this equation implemented in OpenFOAM, and in Fluent it is obviously the same. But I have problems in understanding this equation. For LUDS (linear upwind) we discretize the face value as 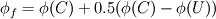 How is the implemented formula connected to that? Thank you very much for an answer in advance! Anne |
Thank you very much for your answer! Meanwhile I have also been able to understand the formula, but it is nice to see the answer here as well.
Have a nice day! Anne |
|
Quote:
" 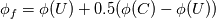 which does not equal the proposed equations." which does not equal the proposed equations." |
One thing got me confused though, in the OpenFOAM website (http://cfd.direct/openfoam/user-guide/fvschemes/), it's written "Some TVD/NVD schemes require a coefficient ψ,0 ≤ ψ ≤ 1 where ψ = 1 corresponds to TVD conformance, usually giving best convergence and ψ = 0 corresponds to best accuracy. Running with ψ = 1 is generally recommended."
So this implies that using ψ = 0 would give the higher order scheme (central difference), which is the opposite stated in dr. Jasak's thesis. I created a new thread with some more questions related to the topic. http://www.cfd-online.com/Forums/ope...tedlinear.html Any thoughts? |
Dear Bazinga and Davi,
I try to derive the implemented formula once again: Two cell centers in upwind flow direction ( 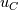 and and 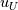 ) are taken into account. The Taylor series leads to the approximation of ) are taken into account. The Taylor series leads to the approximation of  at cells at cells 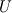 and and 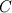 and, subsequently, at face and, subsequently, at face 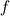 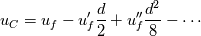 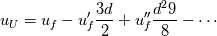 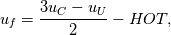 where 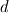 denotes the distance from denotes the distance from 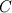 to to 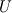 . .The first order upwind approximation is numerically very stable, as the upwind term stabilizes the diagonal of the matrix. Therefore, we use the implicit term of an upwind discretization as a matrix coefficient and add the remaining terms as explicit correction terms on the right-hand side of the equation system. The numerical approximation for the LUDS discretization thus transforms to 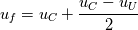 The second term is the explicit correction term. This equals the implemented formula. |
Quote:
Yes, I think what you have written is correct. Because Bazinga mentioned that: CDS for the gradient gives: 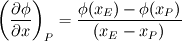 However, this isn't CDS, that was upwind. Also he/she used downwind point (E) for upwind scheme. so I think that was wrong |
Hi guys!
I am making currently some testing with limitedLinear(V) schemes, and I totally see no difference between limiter 0..1! I would expect with limitedLinear 0 to act as linear divergence scheme,am I write? But the results are totally different from "Gauss linear" scheme. I would really appreciate your feedback on this topic. Cheers, Alex |
Quote:
Hi Alexander I haven't tested this, but theoretically yes. you are right. According to this sentence of cfd.direct: limitedLinear: linear scheme that limits towards upwind in regions of rapidly changing gradient; requires a coefficient, where 1 is strongest limiting, tending towards linear as the coefficient tends to 0. https://cfd.direct/openfoam/user-guide/fvschemes/ |
| All times are GMT -4. The time now is 19:10. |