 |
|
|
[Sponsors] | |||||
|
|
|
#61 |
|
Senior Member
Fabian Roesler
Join Date: Mar 2009
Location: Germany
Posts: 213
Rep Power: 18  |
Hi
Well it is the enthalpy method. You use one eulerian grid for both, fluid and solid PCM. Oleinik [1] proposed a weak formulation of the Stefan problem in the 1960s. Based on this approach, Rose [2] and Solomon [3] developed a method based on enthalpy. This is the mother of all enthalpy methods developed since. [1] O. A. Oleinik: A method of solution of the general Stefan problem, Soviet Mathematics, vol. 1, p. 1350–1354, 1960. [2] M. E. Rose: A Method for Calculating Solutions of Parabolic Equations with a Free Boundary, Mathematics of Computation, vol. 14, p. 249–256, 1960. [3] A. D. Solomon: Some Remarks on the Stefan Problem, Mathematics of Computation, vol. 20, p. 347–360, 1966. Hope this is what you were searching for.  Regards Fabian |
|
|
|

|
|
|
|
|
#62 |
|
Member
Thomas Vossel
Join Date: Aug 2013
Location: Germany
Posts: 45
Rep Power: 12  |
Thanks for your answer...
 I guess I was a bit confused with the model and things like the buoyancy term and thus thought that there was some kind of multiphase-flow going on. As the model simplifies things into a one-phase flow there is nothing like that though... 
|
|
|
|

|
|
|
|
|
#63 |
|
New Member
Eric Pernot
Join Date: Apr 2013
Posts: 1
Rep Power: 0  |
Hi everybody,
I would like to update the Rosler's solver to the version 2.2.0 of O.F. Do you know what kind of modifications I have to made for that? Thanking you in advance. Eric |
|
|
|

|
|
|
|
|
#64 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi,
I have an stupid question about post processing. I can plot the alpha (phase fraction) contour in paraview. But I'm wondering how to plot the graph (and export) for comparing as it is not possible in Paraview. |
|
|
|

|
|
|
|
|
#65 |
|
Member
Anja Miehe
Join Date: Dec 2009
Location: Freiberg / Germany
Posts: 48
Rep Power: 16  |
Hello Mohammad,
well, first of all, there are no stupid questions :-). A way I use is only to enable alpha to be shown > in Volume Fields. Then I do a "contour" like you with only one value, 0.5 for example. Split the view and click "Spreadsheet View" for the new one. For the spreadsheet view, only the eye in front of "contour" should be enabled. With the spreadsheet view still active, do "Save Data" and choose "csv" as file type, for example. You will obtain a column file with x,y,z,alpha (not necessarily in that order) that you can plot with gnuplot or other tools to compare the results. If your cases do not vary in geometry, you could compare even a distorted contour plane in 3D using paraview. Only open both cases, create the contour for each case, colour them differently and let them be shown (active eye") in a single 3D view. I hope, this does help you Regards, Anja |
|
|
|

|
|
|
|
|
#66 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Thanks AnjaMiehe.
|
|
|
|

|
|
|
|
|
#67 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi,
I'm trying to update the solid-liquid fraction as mentioned by Voller source based enthalpy method. First, for checking the case I have used just heat conduction. The way I'm trying to solve the energy equation is: volScalarField gamma0 = gamma; //-storing the prev time value do { gamma.storePrevIter(); volScalarField dFdT = 1/(Tl-Ts); volScalarField Finv = gamma*(Tl-Ts)+Ts; volScalarField Sp = -((rho*L)/runTime.deltaTValue())*dFdT; volScalarField Sc = -Sp*Finv + ((rho*L)/runTime.deltaTValue())*(gamma0-gamma); fvScalarMatrix TEqn ( fvm::ddt(rhoCp, T) -fvm::laplacian(K,T) - fvm::Sp(Sp, T) = Sc ); TEqn.solve(); gamma = gamma + dFdT*(T-Finv); gamma = gamma = min(max(gamma,scalar(0)),scalar(1)); Cp = gamma*Cpl+(1-gamma)*Cps; K = gamma*Kl +(1-gamma)*Ks; //- residual calculation of g }while (condition for convergence of g) This the main code for energy equation, and implemented exactly the same case of Gallium error melting just for Test. I'm having the PROBLEM as, PROBLEM (1) Temperature is not updating with time advancing (2) I have switch off (Sp and Sc )to check from where the problem is coming, I saw it's coming from Sp and Sc. (3) I'm wondering whether the loop has any problem ??? I have attached the solver..... PLEASE ADVICE ME TO COME OUT OF THE PROBLEM |
|
|
|

|
|
|
|
|
#68 |
|
Member
Anja Miehe
Join Date: Dec 2009
Location: Freiberg / Germany
Posts: 48
Rep Power: 16  |
Hello Mohammad,
I don't have time right now to look into it, i will try it tomorrow. However, there are some things that make me think about it already now: - Could you provide the equations you based your code on here. I don't have the paper at hand an Voller wrote lots of them ;-) - for dFdt I suppose a linear slope of the fraction of solid, right? But even thought, this is not 1/(Tl-Ts) everywhere, only within the mushy zone. Thus: Code:
dFdt=pos(Tl-T)*pos(T-Ts)/(Tl-Ts) - The old time value is used gamma.oldTime(), no need to store it in an additional variable So much for now, Regards, Anja |
|
|
|

|
|
|
|
|
#69 | |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi AnjaMiehe,
I have attached the equation that I am solving. The paper that I am working on is: http://www.tandfonline.com/doi/abs/1...2#.Up63WkAW1hg Attachment 27158 Quote:
|
||
|
|

|
||
|
|
|
#70 |
|
Member
Anja Miehe
Join Date: Dec 2009
Location: Freiberg / Germany
Posts: 48
Rep Power: 16  |
Hello Mohammad,
to begin with, I am not quite sure if you will like my solution. I have always understood OpenFOAM to code in using grad, div, laplacian ... and not trying to put the discrete equation together with a_p ... Using the Voller paper and your equations I did the following: 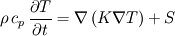 with 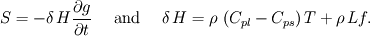 Knowing that 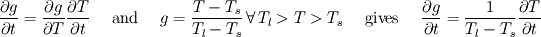 the source term S can be put together in the following way ![S=-\frac{\rho}{T_l-T_s}\left[\left(C_{pl}-C_{ps}\right)T+Lf\right]\frac{\partial T}{\partial t} \,\forall\, T_l > T > T_s. S=-\frac{\rho}{T_l-T_s}\left[\left(C_{pl}-C_{ps}\right)T+Lf\right]\frac{\partial T}{\partial t} \,\forall\, T_l > T > T_s.](/Forums/vbLatex/img/e977c7dc4a3f6ab32fef731fd3735277-1.gif) The equation to be coded is 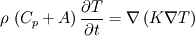 with ![A= \begin{cases} \frac{1}{T_l-T_s}\left[\left(C_{pl}-C_{ps}\right)T+Lf\right] & \,\forall\, T_l>T>T_s \\ 0 \quad & \text{else} \end{cases} A= \begin{cases} \frac{1}{T_l-T_s}\left[\left(C_{pl}-C_{ps}\right)T+Lf\right] & \,\forall\, T_l>T>T_s \\ 0 \quad & \text{else} \end{cases}](/Forums/vbLatex/img/cf3e2f07786b4ce33b419cb5ce06e986-1.gif) The equation is coded in the following way Code:
fvScalarMatrix TEqn
(
(Cp+pos(Tl-T)*pos(T-Ts)*((Cpl-Cps)*T+Lf)/(Tl-Ts))*rho0*fvm::ddt(T)
- fvm::laplacian(fvc::interpolate(K),T)
);
Code:
gamma = (T-Ts)/(Tl-Ts); gamma = min(max(gamma,scalar(0)),scalar(1)); gamma.relax();. Sorry, that I cannot assist you with the exact implementation of the Voller paper. If you want to move on to more complex correlations of gamma to temperature, you could try to read in an interpolation table. See this link for more information: http://www.cfd-online.com/Forums/ope...ies-false.html Regards, Anja |
|
|
|

|
|
|
|
|
#71 |
|
Member
Thomas Vossel
Join Date: Aug 2013
Location: Germany
Posts: 45
Rep Power: 12  |
Well I'm currently writing my masters thesis about this topic and I got something running that works (although has to be revamped at certain places to include additional features). My problem is about the flow and solidification of an alloy though but as I'm right now changing the temperature calculations in order to correctly take care of the eutectic solidification I can post how I'm doing things right now. My solver's design also is based on Voller's enthalpy-porosity-model but I'm not really copying a certain paper 1:1...
But oh well here is the code of my TEqn.H file which calculates the new temperature field: Code:
// initialize and solve energy equation
fvScalarMatrix TEqn
(
cpEff * fvm::ddt(Temp)
+ fvm::div(phib * fvc::interpolate(cpMean), Temp, "div(phib*cpEff,Temp)")
- fvm::laplacian(lambda / rhob, Temp, "laplacian(lambda|rhob,Temp)")
);
TEqn.relax();
TEqn.solve();
Code:
forAll(fracSol, celli)
{
// update cpMean, cpEff and lambda
if (Temp[celli] < TbSol.value() )
{
cpMean[celli] = cpbSol.value();
cpEff[celli] = cpMean[celli];
}
else if (Temp[celli] > TbLiq.value() )
{
cpMean[celli] = cpbLiq.value();
cpEff[celli] = cpMean[celli];
}
else
{
cpMean[celli] = fracSol[celli] * cpbSol.value() + (1.0 - fracSol[celli]) * cpbLiq.value();
cpEff[celli] = cpMean[celli] + Lb.value() * ( 1.0 / TbDelta.value() ); // currently Lb gets multiplied with constant slope of fake linear function for fracSol
// -> replace with real slope term later on (plus in setInitialFracSol.H (now probably not used anymore) )
}
lambda[celli] = fracSol[celli] * lambdabSol.value() + (1.0 - fracSol[celli]) * lambdabLiq.value();
// calculate fracSol depending on chosen method
if (fracSolMethod == "dataBased")
{
// Info << "fraction solid calculated via dataBased method" << endl;
// only do the calculations when temperature is between TLiq and TSol
// otherwise the values 0 and 1 can be set directly
if (Temp[celli] < TbSol.value() )
{
fracSol[celli] = 1.0;
}
else if (Temp[celli] > TbLiq.value() )
{
fracSol[celli] = 0;
}
else
{
// fracSol right now uses a "fake" linear function meant to be replaced later on by a method which grabs fracSol(T) values from a table
fracSol[celli] = (-1.0 / TbDelta.value() ) * (Temp[celli] - TbSol.value() ) + 1;
}
}
|
|
|
|

|
|
|
|
|
#72 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi,
I have implemented the method that I mentioned. It's working now and giving the correct value. Now I have some things to dig out: (1)Anyone please suggest me, how can I find out the interface velocity ? (I want to calculate the interface velocity in the solver ) (2) Have anyone worked with the non equillibrium solidification considering the under cooling ? cheers |
|
|
|

|
|
|
|
|
#73 |
|
Member
Thomas Vossel
Join Date: Aug 2013
Location: Germany
Posts: 45
Rep Power: 12  |
Have a look at the fvc::interpolate(...) and fvc::reconstruct(...) commands in order to get surface values and reconstruct them into cell values. You can see them in use in for example the twoPhaseEulerFoam solver...
|
|
|
|

|
|
|
|
|
#74 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi,
I'm little bit of puzzle of a term. Please help me to correct the definition: In the energy equation: d/dt(rho*Cp T) + div(rho U Cp T) = laplacian(K T) + ST, I am a bit of concern about the source term, whether it be... (1) ST = rho*L*d/dt(gamma), ONLY THE LATENT HEAT PRODUCT OR (2) ST = dH*d/dt(gamma), where dH = rho*(Cl-Cs)*(T-Tref)+rho* L. Where, Cl = liquid specific heat and Cs is the solid specific heat. |
|
|
|

|
|
|
|
|
#75 |
|
Member
Anja Miehe
Join Date: Dec 2009
Location: Freiberg / Germany
Posts: 48
Rep Power: 16  |
Hello Mohammad,
you probably find it confusing but both is right in its own way. If you start form the energy conservation equation in form of enthalpy, the question is, how you define the relation between temperature and energy.
##### For you question how to get the interface velocity: take a look at the definition of the VoF function. There it is 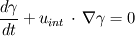 , where 0 is only true for a system without phase change. If the phases are liquid and solid of one material, for example, the right hand side of the equation yields the rate of phase change. u_int is than: , where 0 is only true for a system without phase change. If the phases are liquid and solid of one material, for example, the right hand side of the equation yields the rate of phase change. u_int is than: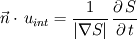 which is the normal component of the interface. I guess, you aim onto the cooling rate, if so, you only need the normal component. Take care when coding, avoid to divide by zero outside the mushy zone where f_l, f_s (both can be inserted for S) do not change and the gradient in the denominator is zero. By the way, you get this equation style using [ math ] ... [ / math ] without the spacings, and you simply write your equation in Latex style. Simply click on one of the equations to see that. Have a nice day, Anja |
|
|
|

|
|
|
|
|
#76 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi,
I have a query about the Fabian Gallium test case. I have seen that, in the fvSolution file, the solver has been chosen for p_rgh and T , but not for U. Can any one please explain the reason behind it ? in fvSolution file: Code:
solvers
{
p_rgh
{
solver PCG;
preconditioner DIC;
tolerance 1e-8;
relTol 0.01;
}
p_rghFinal
{
$p_rgh;
relTol 0;
}
T
{
solver PBiCG;
preconditioner DILU;
tolerance 1e-7;
relTol 0.1;
}
TFinal
{
solver PBiCG;
preconditioner DILU;
tolerance 1e-10;
relTol 0;
}
}
|
|
|
|

|
|
|
|
|
#77 |
|
Member
Anja Miehe
Join Date: Dec 2009
Location: Freiberg / Germany
Posts: 48
Rep Power: 16  |
Hello Mohammad,
do please take a look at posts No #31,#32 of this thread. Fabian is giving an idea about it there. Regards, Anja |
|
|
|

|
|
|
|
|
#78 |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 14  |
Hi Anja Miehe,
Sorry it's me again. In my solver, I want to account for temperature dependent thermo-physical properties during melting/solidification. The governing equation that I'm solving is similar to Fabian and as follows, 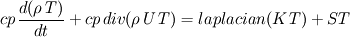 and the source term is updated as iterative procedure as stated by Voller, like Sp and Sc. And at each iteration I'm updating the liquid fraction. Until now it works fine, and I have also validated the case with Gallium melting. The result is good. But the problem I'm facing now is to work with the temperature dependent thermo-physical properties. The code diverges after 2/3 time steps. I'm sure, the way I am working with the temperature dependent properties are not correct. Please give me some advice to deal with the temperature dependent thermo-physical properties in the case of melting/solidification problem. **My solver and case file is attached. Thanks in advance |
|
|
|

|
|
|
|
|
#79 |
|
Member
Anja Miehe
Join Date: Dec 2009
Location: Freiberg / Germany
Posts: 48
Rep Power: 16  |
Hello Mohammad,
no need to be sorry, I am glad when I can help. Good to see that you found a way to code the Voller scheme like you intended. Well done. I did not try to compile your code as I am already in my Christmas Holidays and have only my little home laptop with me. Nonetheless, there are some things striking me.
Code:
relaxationFactors
{
fields
{
"(alpha).*" 0.1;
"(p_rgh).*" 0.3;
}
equations
{
default 0.7;
"(T).*" 0.7;
"(U).*" 0.7;
}
}
I hope, this will do it already. Regards and happy Xmas, Anja |
|
|
|

|
|
|
|
|
#80 | |
|
Senior Member
Fabian Roesler
Join Date: Mar 2009
Location: Germany
Posts: 213
Rep Power: 18  |
Hi all
First of all, sorry for backing out from the very nice discussion in this thread in the last few months. I was packing together my thesis. But now it is officially submitted and two months of vacation are over. I appreciate that the solid/liquid phase change topic is still strongly represented in this forum and I am happy that Anja and Mohammad shared their solvers with us. I went through all of your posts and there is the topics of the iterative correction of the liquid fraction that should be discussed. The method used in Anjas Solver (Post 70) is iterating the energy conservation equation but is not correcting the liquid fraction. I recommend this early Voller paper to understand the necessity of the iterative update: Quote:
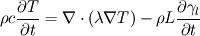 (1) (1)is discretized as follows: ![\left[ {{a}_{p}}+{{\left( \rho cV \right)}_{p}} \right]T_{p}^{{}}={{\left( \rho cV \right)}_{p}}T_{p}^{old}+\sum\limits_{nb}{{{a}_{nb}}T_{nb}^{{}}}+{{\left( \rho cV \right)}_{p}}\left[ \gamma _{l,p}^{old}-\gamma _{l,p}^{{}} \right] \left[ {{a}_{p}}+{{\left( \rho cV \right)}_{p}} \right]T_{p}^{{}}={{\left( \rho cV \right)}_{p}}T_{p}^{old}+\sum\limits_{nb}{{{a}_{nb}}T_{nb}^{{}}}+{{\left( \rho cV \right)}_{p}}\left[ \gamma _{l,p}^{old}-\gamma _{l,p}^{{}} \right]](/Forums/vbLatex/img/e2ec4706e209e2c627250b04f368e8e1-1.gif) (2) (2)As gamma is calculated from temperature, this algebraic equation is non linear. Voller linearized it using an iterative method: ![\left[ {{a}_{p}}+{{\left( \rho cV \right)}_{p}} \right]T_{p}^{m+1}={{\left( \rho cV \right)}_{p}}T_{p}^{old}+\sum\limits_{nb}{{{a}_{nb}}T_{nb}^{m+1}}+{{\left( \rho cV \right)}_{p}}\left[ \gamma _{l,p}^{old}-\gamma _{l,p}^{m} \right] \left[ {{a}_{p}}+{{\left( \rho cV \right)}_{p}} \right]T_{p}^{m+1}={{\left( \rho cV \right)}_{p}}T_{p}^{old}+\sum\limits_{nb}{{{a}_{nb}}T_{nb}^{m+1}}+{{\left( \rho cV \right)}_{p}}\left[ \gamma _{l,p}^{old}-\gamma _{l,p}^{m} \right]](/Forums/vbLatex/img/8237bbfee40299a4bd63d5cfd39304d2-1.gif) (3) (3)This equation can now be solved with any code (like OpenFOAM). However, as the source term was linearized, temperature,liquid fraction and enthalpy don not necessarily have to correlate. For this purpose, within the iterative procedure, a correction of the liquid fraction has to be performed. Have a look at the attached picture. When enthalpy is conserved, the following is correct: 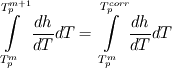 or or 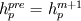 (4) (4)Substituting the enthalpy temperature correlation 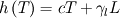 (5) (5)into (4) leads to the equation to calculate the corrected liquid fraction: 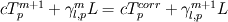 or or 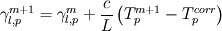 (6) (6)The steeper the slope of the enthalpy-temperature during phase change, the more unstable gets this method. Thus, equation (6) has to be under-relaxed leading to 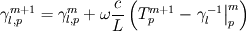 (7) (7)with omega in the range of 0.6 to 0.8. However, one can consider the whole term in front of the brackets as under-relaxation factor which is much smaller. During iteration, the bracket will turn to zero as 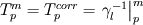 (8) (8)So this is the iterative correction of the liquid fraction. However, this method will lead to nonsense when the energy conservation equation is not solved at least once per iteration step. In standard OpenFOAM, one can not give a minimum number of iterations in the fvSolution dictionary. So there are two possibilities to still achieve at least one iteration:
Never the less I would like to share the basic solver on which the solver from my thesis is founded as well as the necessary changes in the ldu matrix solvers to use the code in an efficient way. Extract the data inside the convMeltFoam.tar.gz and run the install script. This will provide the changes inside the ldu matrix solvers, compile OpenFOAM src to make the changes and install the solver. However, be careful as this script will only run with OF 2.2.x. Cheers 
|
||
|
|

|
||
 |
| Tags |
| melting openfoam |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Melting and solidification with free surface problem? | cqlwj123 | CFX | 6 | July 25, 2013 02:46 |
| Can I solve this problem by Fluent? | Kai_kc | FLUENT | 1 | October 27, 2010 05:29 |
| natural convection problem for a CHT problem | Se-Hee | CFX | 2 | June 10, 2007 06:29 |
| Adiabatic and Rotating wall (Convection problem) | ParodDav | CFX | 5 | April 29, 2007 19:13 |
| Melting Problem | M | FLUENT | 0 | April 29, 2007 16:07 |