A roughness-dependent model
From CFD-Wiki
Contents |
Two-equation 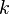 -
- eddy viscosity model
eddy viscosity model
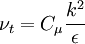 | (1) |
where:
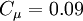
One-equation eddy viscosity model
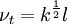 | (2) |
Algebraic eddy viscosity model
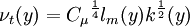 | (3) |
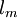 is the mixing length.
is the mixing length.
Algebraic model for the turbulent kinetic energy
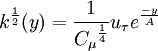 | (4) |
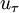 is the shear velocity and
is the shear velocity and 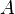 a model parameter.
a model parameter.
Algebraic model for the mixing length, based on (4) [Absi (2006)]
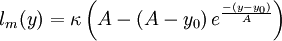 | (5) |
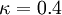 ,
, 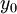 is the hydrodynamic roughness
is the hydrodynamic roughness
the algebraic eddy viscosity model is therefore
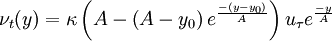 | (6) |
for a smooth wall (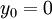 ):
):
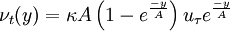 | (7) |
References
- Absi, R. (2006), "A roughness and time dependent mixing length equation", Journal of Hydraulic, Coastal and Environmental Engineering, Japan Society of Civil Engineers, (Doboku Gakkai Ronbunshuu B), Vol. 62, No. 4, pp.437-446.
