Algebraic turbulence models
From CFD-Wiki
m (Zero equation models moved to Zero equation turbulence models) |
(small addition) |
||
| Line 1: | Line 1: | ||
| - | Zero equation [[Turbulence modeling|turbulence models]] are models that do not require the solution of any additional equations, and are calculated directly from the flow variables. | + | Zero equation [[Turbulence modeling|turbulence models]] are models that do not require the solution of any additional equations, and are calculated directly from the flow variables. As a consequence zero eqation models are local in nature and can not account for any history effects on the turbulence, like convection and diffusion of turbulent energy. These models are often too simple for use in general situations, but can be quite useful for simpler flow geometries or in start-up situations (e.g. the initial phases of a computation in which a more complicated model may have difficulties). The two most well known zero equation models are the |
*[[Baldwin-Lomax model]] and the | *[[Baldwin-Lomax model]] and the | ||
Revision as of 21:02, 9 May 2006
Zero equation turbulence models are models that do not require the solution of any additional equations, and are calculated directly from the flow variables. As a consequence zero eqation models are local in nature and can not account for any history effects on the turbulence, like convection and diffusion of turbulent energy. These models are often too simple for use in general situations, but can be quite useful for simpler flow geometries or in start-up situations (e.g. the initial phases of a computation in which a more complicated model may have difficulties). The two most well known zero equation models are the
- Baldwin-Lomax model and the
- Cebeci-Smith model.
Other even simpler models, such a models written as 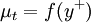 , are sometimes used in particular situations (e.g. boundary layers or jets).
, are sometimes used in particular situations (e.g. boundary layers or jets).
