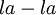Approximation Schemes for convective term - structured grids - Summary of Discretizations Schemes and examples
From CFD-Wiki
When we shall fill this page, I offer to make common identifications, because in different issues was used different notation.
Also we beg everybody to help me with original works. Later I shall write, what is necessary. If anyone have literature connected with convective schemes, please drop me a line.
We shall be very glad and grateful to hear any critical suggestion (please drop a few lines at Wiki Forum)
It is just a skeleton, but we hope that it will be developed into the good thing
Contents |
Discretizations Schemes Estimation of order
Discretizations Schemes Estimation of error
Selection advice
Comparison of Discretizations Schemes
Numerical examples
Pure convection of a scalar step by a rotating velocity field (Smith-Hutton test)
R.M.Smith and A.G.Hutton (1982), "The numerical treatment of advection: A performance comparison of current methods", Numerical Heat Transfer, Vol. 5, p439.
This was the test problem devised for evaluating a range of numerical models of convection at the third meeting of the International Association for Hydraulic Research Working Group on Refined Modelling of flow
Sometimes it was used scalar profile with a discontinuity at 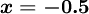
We shall use here more smooth inlet profile
|
| (1) |
Square Lid-driven cavity flow
Example code for solving Smith-Hutton test
Dear friends
It's just a scrap. Later I'll correct it, although it's a complete working code
Michail
Sample code for solving Smith-Hutton test - Fortran 90
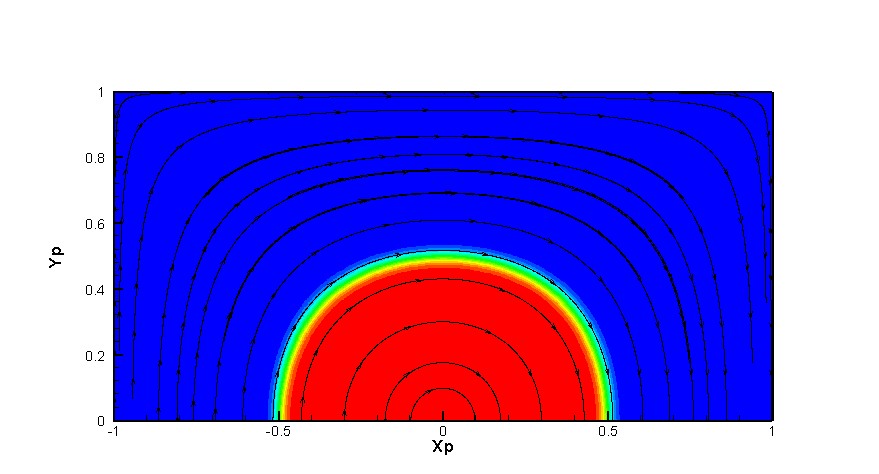
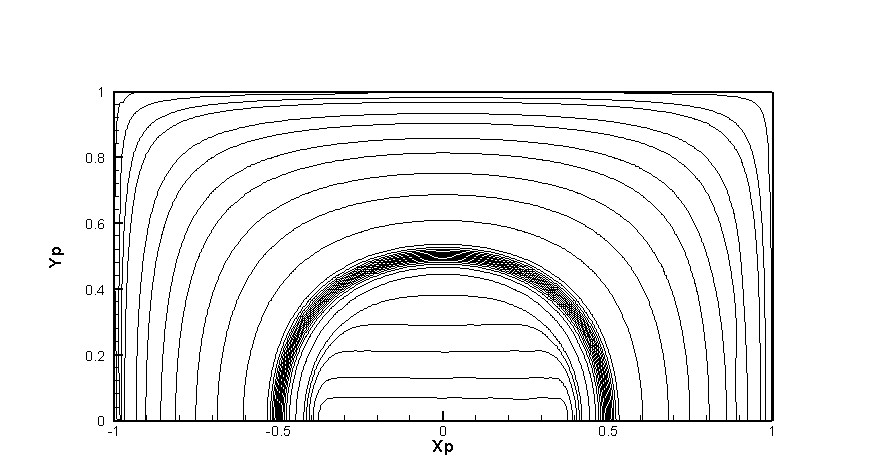
It's a results, obtained using this code (UDS and HLPA schemes)
Below it's cleary seen the numerical diffusion impact, comparing the contour fields obtaining using the UDS and HLPA. A bit later we shall place here a solution gained with QUICK scheme, and it will be seen the osscilations.