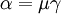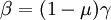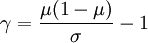Beta PDF
From CFD-Wiki
(Difference between revisions)
| Line 6: | Line 6: | ||
The beta function PDF has the form | The beta function PDF has the form | ||
:<math> | :<math> | ||
| - | P (\eta) = \frac{\eta^\alpha (1- \eta)^{\beta-1}}{\Gamma(\alpha) \Gamma(\beta)} | + | P (\eta) = \frac{\eta^\{alpha-1} (1- \eta)^{\beta-1}}{\Gamma(\alpha) \Gamma(\beta)} |
\Gamma(\alpha + \beta) | \Gamma(\alpha + \beta) | ||
</math> | </math> | ||
Revision as of 08:59, 27 July 2007
A  probability density function depends on
two moments only; the mean
probability density function depends on
two moments only; the mean 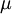 and the variance
and the variance 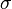 .
This function is widely used in turbulent combustion to define the scalar distribution at each
computational point as a function of the mean and variance.
Assuming that the sample space of the scalar varies betwen 0 and 1.
The beta function PDF has the form
.
This function is widely used in turbulent combustion to define the scalar distribution at each
computational point as a function of the mean and variance.
Assuming that the sample space of the scalar varies betwen 0 and 1.
The beta function PDF has the form
- Failed to parse (syntax error): P (\eta) = \frac{\eta^\{alpha-1} (1- \eta)^{\beta-1}}{\Gamma(\alpha) \Gamma(\beta)} \Gamma(\alpha + \beta)
where 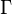 is the gamma function and the parameters
is the gamma function and the parameters
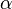 and
and  are related through
are related through
where 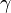 is
is