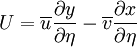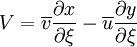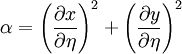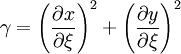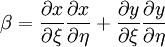Calculation on non-orthogonal curvelinear structured grids, finite-volume method
From CFD-Wiki
(Difference between revisions)
(→2D case) |
(→2D case) |
||
| Line 37: | Line 37: | ||
</math> | </math> | ||
</td><td width="5%">(6)</td></tr></table> | </td><td width="5%">(6)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | \beta = \frac{\partial x}{ \partial \xi} \frac{\partial x}{ \partial \eta} + \frac{\partial y}{ \partial \xi} \frac{\partial y}{ \partial \eta} | ||
| + | </math> | ||
| + | </td><td width="5%">(7)</td></tr></table> | ||
Revision as of 07:04, 18 August 2010
2D case
For calculations in complex geometries boundary-fitted non-orthogonal curvlinear grids is usually used.
General transport equation is transformed from the physical domain 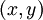 into the computational domain
into the computational domain 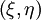 as the following equation
as the following equation
|
| (2) |
where
|
| (3) |
|
| (4) |
|
| (5) |
|
| (6) |
|
| (7) |

![\frac{\partial}{\partial \xi} \left( \rho U \phi \right) + \frac{\partial }{ \partial \eta } \left( \rho V \phi \right) = \frac{\partial}{\partial \xi} \left[ \frac{\Gamma }{J} \left( \alpha \frac{\partial \phi}{\partial \xi} - \beta \frac{\partial \phi}{ \partial \eta} \right) \right] + \frac{\partial}{\partial \eta} \left[ \frac{\Gamma}{J} \left( \gamma \frac{\partial \phi}{\partial \eta} - \beta \frac{\partial \phi}{ \partial \xi} \right) \right] + J S^{\phi}](/W/images/math/3/8/2/382456ea15e881910f1b040f17a347bd.png)