Calculation on non-orthogonal curvelinear structured grids, finite-volume method
From CFD-Wiki
(Difference between revisions)
(→2D case) |
(→2D case) |
||
| (11 intermediate revisions not shown) | |||
| Line 25: | Line 25: | ||
</math> | </math> | ||
</td><td width="5%">(4)</td></tr></table> | </td><td width="5%">(4)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | \alpha = \left( \frac{\partial x}{\partial \eta } \right)^2 + \left( \frac{\partial y}{\partial \eta } \right)^2 | ||
| + | </math> | ||
| + | </td><td width="5%">(5)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | \gamma = \left( \frac{\partial x}{ \partial \xi } \right)^2 + \left( \frac{\partial y}{ \partial \xi } \right)^2 | ||
| + | </math> | ||
| + | </td><td width="5%">(6)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | \beta = \frac{\partial x}{ \partial \xi} \frac{\partial x}{ \partial \eta} + \frac{\partial y}{ \partial \xi} \frac{\partial y}{ \partial \eta} | ||
| + | </math> | ||
| + | </td><td width="5%">(7)</td></tr></table> | ||
| + | |||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | J = \frac{\partial x}{ \partial \xi} \frac{\partial y}{ \partial \eta} - \frac{\partial y}{ \partial \xi} \frac{\partial x}{ \partial \eta} | ||
| + | </math> | ||
| + | </td><td width="5%">(8)</td></tr></table> | ||
| + | |||
| + | Using the finite volume method the trnsformed equations can be integrated as follows: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | \left[ \left( \rho U \Delta \eta \right) \right]^{e}_{w} + \left[ \left( \rho V \Delta \xi \right) \right]^{n}_{s} = \left[ \frac{\Gamma \Delta \eta}{J} \left( \alpha \frac{\partial \phi}{\partial \xi} - \beta \frac{\partial \phi}{ \partial \eta} \right) \right]^{e}_{w} + \left[ \frac{\Gamma \Delta \xi}{J} \left( \gamma \frac{\partial \phi}{\partial \eta } - \beta \frac{\partial \phi}{\partial \xi} \right) \right]^{n}_{s} + \left( J \Delta \xi \Delta \eta \right) \overline{S}^{\phi}_{P} | ||
| + | </math> | ||
| + | </td><td width="5%">(9)</td></tr></table> | ||
| + | |||
| + | The convection terms are approximated as described in section http://www.cfd-online.com/Wiki/Discretization_of_the_convection_term . | ||
| + | |||
| + | Diffusion terms are approximated by the second-oder central differencing scheme. | ||
| + | |||
| + | The standard form of the finite volume equation can be obtained as | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | A^{\phi}_{P} \phi_{P} = A^{\phi}_{E} \phi_{E} + A^{\phi}_{W} \phi_{W} + A^{\phi}_{N} \phi_{N} + A^{\phi}_{S} \phi_{S} + b^{\phi} | ||
| + | </math> | ||
| + | </td><td width="5%">(10)</td></tr></table> | ||
| + | |||
| + | where | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | A^{\phi}_{E} = \left(\frac{\Gamma}{J} \alpha \frac{\Delta \eta}{\Delta \xi} \right)_{e} + max \left[ 0, - \left( \rho U \Delta \eta \right)_{e} \right] | ||
| + | </math> | ||
| + | </td><td width="5%">(11)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | A^{\phi}_{W} = \left(\frac{\Gamma}{J} \alpha \frac{\Delta \eta}{\Delta \xi} \right)_{w} + max \left[ 0, \left( \rho U \Delta \eta \right)_{w} \right] | ||
| + | </math> | ||
| + | </td><td width="5%">(12)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | A^{\phi}_{N} = \left( \frac{ \Gamma }{J} \gamma \frac{\Delta \xi}{\Delta \eta} \right)_{n} + max \left[ 0, - \left( \rho V \Delta \xi \right)_{n} \right] | ||
| + | </math> | ||
| + | </td><td width="5%">(13)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | A^{\phi}_{S} = \left( \frac{ \Gamma }{J} \gamma \frac{\Delta \xi}{\Delta \eta} \right)_{s} + max \left[ 0, \left( \rho V \Delta \xi \right)_{s} \right] | ||
| + | </math> | ||
| + | </td><td width="5%">(14)</td></tr></table> | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | b^{\phi} = \left( J \Delta \xi \Delta \eta \right) \overline{S}^{\phi}_{P} - \left[ \frac{\Gamma \Delta \eta}{J} \left( \beta \frac{\partial \phi}{\partial \eta} \right) \right]^{e}_{w} - \left[ \frac{\Gamma \Delta \xi}{J} \left( \beta \frac{\partial \phi}{\partial \xi} \right) \right]^{n}_{s} | ||
| + | </math> | ||
| + | </td><td width="5%">(15)</td></tr></table> | ||
Latest revision as of 10:24, 20 August 2010
2D case
For calculations in complex geometries boundary-fitted non-orthogonal curvlinear grids is usually used.
General transport equation is transformed from the physical domain 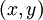 into the computational domain
into the computational domain 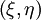 as the following equation
as the following equation
|
| (2) |
where
|
| (3) |
|
| (4) |
|
| (5) |
|
| (6) |
|
| (7) |
|
| (8) |
Using the finite volume method the trnsformed equations can be integrated as follows:
|
| (9) |
The convection terms are approximated as described in section http://www.cfd-online.com/Wiki/Discretization_of_the_convection_term .
Diffusion terms are approximated by the second-oder central differencing scheme.
The standard form of the finite volume equation can be obtained as
|
| (10) |
where
|
| (11) |
|
| (12) |
|
| (13) |
|
| (14) |
|
| (15) |

![\frac{\partial}{\partial \xi} \left( \rho U \phi \right) + \frac{\partial }{ \partial \eta } \left( \rho V \phi \right) = \frac{\partial}{\partial \xi} \left[ \frac{\Gamma }{J} \left( \alpha \frac{\partial \phi}{\partial \xi} - \beta \frac{\partial \phi}{ \partial \eta} \right) \right] + \frac{\partial}{\partial \eta} \left[ \frac{\Gamma}{J} \left( \gamma \frac{\partial \phi}{\partial \eta} - \beta \frac{\partial \phi}{ \partial \xi} \right) \right] + J S^{\phi}](/W/images/math/3/8/2/382456ea15e881910f1b040f17a347bd.png)
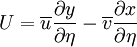
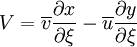
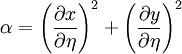
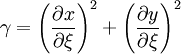
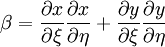
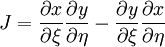
![\left[ \left( \rho U \Delta \eta \right) \right]^{e}_{w} + \left[ \left( \rho V \Delta \xi \right) \right]^{n}_{s} = \left[ \frac{\Gamma \Delta \eta}{J} \left( \alpha \frac{\partial \phi}{\partial \xi} - \beta \frac{\partial \phi}{ \partial \eta} \right) \right]^{e}_{w} + \left[ \frac{\Gamma \Delta \xi}{J} \left( \gamma \frac{\partial \phi}{\partial \eta } - \beta \frac{\partial \phi}{\partial \xi} \right) \right]^{n}_{s} + \left( J \Delta \xi \Delta \eta \right) \overline{S}^{\phi}_{P}](/W/images/math/c/9/b/c9bc323ba9595d8d85677016f4e53536.png)
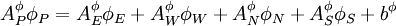
![A^{\phi}_{E} = \left(\frac{\Gamma}{J} \alpha \frac{\Delta \eta}{\Delta \xi} \right)_{e} + max \left[ 0, - \left( \rho U \Delta \eta \right)_{e} \right]](/W/images/math/d/d/3/dd391b55e6d5ab853dfb8a363e1ad14e.png)
![A^{\phi}_{W} = \left(\frac{\Gamma}{J} \alpha \frac{\Delta \eta}{\Delta \xi} \right)_{w} + max \left[ 0, \left( \rho U \Delta \eta \right)_{w} \right]](/W/images/math/0/d/b/0dbf08dd7c67f1ce5b898703ed51ba9e.png)
![A^{\phi}_{N} = \left( \frac{ \Gamma }{J} \gamma \frac{\Delta \xi}{\Delta \eta} \right)_{n} + max \left[ 0, - \left( \rho V \Delta \xi \right)_{n} \right]](/W/images/math/7/c/1/7c191e197bd433da99e710d3972cb506.png)
![A^{\phi}_{S} = \left( \frac{ \Gamma }{J} \gamma \frac{\Delta \xi}{\Delta \eta} \right)_{s} + max \left[ 0, \left( \rho V \Delta \xi \right)_{s} \right]](/W/images/math/3/8/3/383089c82dad52e5e81f6a38822a7428.png)
![b^{\phi} = \left( J \Delta \xi \Delta \eta \right) \overline{S}^{\phi}_{P} - \left[ \frac{\Gamma \Delta \eta}{J} \left( \beta \frac{\partial \phi}{\partial \eta} \right) \right]^{e}_{w} - \left[ \frac{\Gamma \Delta \xi}{J} \left( \beta \frac{\partial \phi}{\partial \xi} \right) \right]^{n}_{s}](/W/images/math/6/7/9/679e9d836ee26246cc251d1718a29333.png)