Code: Lid driven cavity using pressure free velocity form
From CFD-Wiki
m (→Lid-driven cavity Matlab script) |
m (moved Lid driven cavity using pressure free velocity form to Code: Lid driven cavity using pressure free velocity form: name consistency) |
||
| (3 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==Lid-driven cavity using pressure-free velocity formulation== | ==Lid-driven cavity using pressure-free velocity formulation== | ||
| + | |||
| + | This sample code uses four-node simple-cubic finite elements and simple iteration. | ||
===Theory=== | ===Theory=== | ||
| Line 11: | Line 13: | ||
Equivalent weak or variational forms of the equations, proved to produce the same velocity solution as the Navier-Stokes equation are | Equivalent weak or variational forms of the equations, proved to produce the same velocity solution as the Navier-Stokes equation are | ||
| - | :<math>(\mathbf{w},\frac{\partial\mathbf{v}}{\partial t})=-(\mathbf{w},\mathbf{v}\cdot\nabla\mathbf{v})-\nu(\nabla\mathbf{w}: \nabla\mathbf{v})+(\mathbf{w},\mathbf{f}^S)</math> | + | :<math>(\mathbf{w},\frac{\partial\mathbf{v}}{\partial t})=-(\mathbf{w},\mathbf{v}\cdot\nabla\mathbf{v})-\nu(\nabla\mathbf{w}: \nabla\mathbf{v})+(\mathbf{w},\mathbf{f}^S)</math>, |
:<math>(\mathbf{g}_i,\nabla p)=-(\mathbf{g}_i,\mathbf{v}\cdot\nabla\mathbf{v}_j)-\nu(\nabla\mathbf{g}_i: \nabla\mathbf{v}_j)+(\mathbf{g}_i,\mathbf{f}^I)\,</math>, | :<math>(\mathbf{g}_i,\nabla p)=-(\mathbf{g}_i,\mathbf{v}\cdot\nabla\mathbf{v}_j)-\nu(\nabla\mathbf{g}_i: \nabla\mathbf{v}_j)+(\mathbf{g}_i,\mathbf{f}^I)\,</math>, | ||
| Line 18: | Line 20: | ||
In the discrete case, it is desirable to choose basis functions for the velocity which reflect the essential feature of incompressible flow — the velocity elements must be divergence-free. While the velocity is the variable of interest, the existence of the stream function or vector potential is necessary by the Helmholtz Theorem. Further, to determine fluid flow in the absence of a pressure gradient, one can specify the difference of stream function values across a 2D channel, or the line integral of the tangential component of the vector potential around the channel in 3D, the flow being given by Stokes' Theorem. This leads naturally to the use of Hermite stream function (in 2D) or velocity potential elements (in 3D). | In the discrete case, it is desirable to choose basis functions for the velocity which reflect the essential feature of incompressible flow — the velocity elements must be divergence-free. While the velocity is the variable of interest, the existence of the stream function or vector potential is necessary by the Helmholtz Theorem. Further, to determine fluid flow in the absence of a pressure gradient, one can specify the difference of stream function values across a 2D channel, or the line integral of the tangential component of the vector potential around the channel in 3D, the flow being given by Stokes' Theorem. This leads naturally to the use of Hermite stream function (in 2D) or velocity potential elements (in 3D). | ||
| - | Involving, as it does, both stream function and velocity degrees-of-freedom, the method might be called a velocity-stream function or stream function-velocity method. | + | Involving, as it does, both stream function and velocity degrees-of-freedom, the method might be called a '''velocity-stream function''' or '''stream function-velocity''' method. |
We now restrict discussion to 2D continuous Hermite finite elements which have at least first-derivative degrees-of-freedom. With this, one can draw a large number of candidate triangular and rectangular elements from the plate-bending literature. These elements have derivatives as components of the gradient. In 2D, the gradient and curl of a scalar are clearly orthogonal, given by the expressions, | We now restrict discussion to 2D continuous Hermite finite elements which have at least first-derivative degrees-of-freedom. With this, one can draw a large number of candidate triangular and rectangular elements from the plate-bending literature. These elements have derivatives as components of the gradient. In 2D, the gradient and curl of a scalar are clearly orthogonal, given by the expressions, | ||
| Line 33: | Line 35: | ||
The algebraic equations to be solved are simple to set up, but of course are non-linear, requiring iteration of the linearized equations. | The algebraic equations to be solved are simple to set up, but of course are non-linear, requiring iteration of the linearized equations. | ||
| - | The finite elements we will use here are apparently due to Melosh [3], but can also be found in Zienkiewitz [4]. These simple cubic-complete elements have three degrees-of-freedom at each of the four nodes. In the sample code we use this Hermite element for the pressure, and the modified form obtained by interchanging derivatives and the sign of one of them (though a simple bilinear element could be used for the pressure as well). The degrees-of-freedom are the pressure and pressure gardient, and the stream function and components of the solenoidal velocity for the modified element. | + | The finite elements we will use here are apparently due to Melosh [3], but can also be found in Zienkiewitz [4]. These simple cubic-complete elements have three degrees-of-freedom at each of the four nodes. In the sample code we use this Hermite element for the pressure, and the modified form obtained by interchanging derivatives and the sign of one of them (though a simple bilinear element could be used for the pressure as well). The degrees-of-freedom are the pressure and pressure gardient, and the stream function and components of the solenoidal velocity for the modified element. The normal component of the velocity is continuous at element interfaces as is required, but the tangential velocity component may not be continuous. |
The code implementing the lid-driven cavity problem is written for Matlab. The script below is problem-specific, and calls problem-independent functions to evaluate the element diffusion and convection matricies and evaluate the pressure from the resulting velocity field. These three functions accept general quadrilateral elements with straight sides as well as the rectangular elements used here. Other functions are a GMRES iterative solver using ILU preconditioning and incorporating the essential boundary conditions, and a function to produce non-uniform nodal spacing for the problem mesh. | The code implementing the lid-driven cavity problem is written for Matlab. The script below is problem-specific, and calls problem-independent functions to evaluate the element diffusion and convection matricies and evaluate the pressure from the resulting velocity field. These three functions accept general quadrilateral elements with straight sides as well as the rectangular elements used here. Other functions are a GMRES iterative solver using ILU preconditioning and incorporating the essential boundary conditions, and a function to produce non-uniform nodal spacing for the problem mesh. | ||
| - | This "educational code" is a simplified version of the code used in [1]. The user interface is the code itself. The user can experiment with changing the mesh, the Reynolds number, and the number of nonlinear iterations performed, as well as the relaxation factor. There are suggestions in the code regarding near-optimum choices for this factor as a function of Reynolds number. These values are given in the paper as well. | + | This "educational code" is a simplified version of the code used in [1]. The user interface is the code itself. The user can experiment with changing the mesh, the Reynolds number, and the number of nonlinear iterations performed, as well as the relaxation factor. There are suggestions in the code regarding near-optimum choices for this factor as a function of Reynolds number. These values are given in the paper as well. For larger Reynolds numbers, a smaller relaxation factor speeds up convergence by smoothing the velocity factor <math>(\mathbf{v}\cdot\nabla)</math> in the convection term, but will impede convergence if made too small. |
The output consists of graphic plots of contour levels of the stream function and the pressure levels. | The output consists of graphic plots of contour levels of the stream function and the pressure levels. | ||
| Line 473: | Line 475: | ||
==references== | ==references== | ||
| - | [1] {{reference-paper |author = Holdeman, J. T. |year = 2010 | title = A Hermite finite element method for incompressible fluid flow | rest = Int. J. Numer. Meth. Fluids, '''64''':376-408 }} | + | [1] {{reference-paper |author = Holdeman, J. T. |year = 2010 | title = A Hermite finite element method for incompressible fluid flow | rest = Int. J. Numer. Meth. Fluids, '''64''': 376-408 }} |
| - | [2] {{reference-paper |author = Holdeman, J. T. |year = 2010 | title = Computation of incompressible thermal flows using Hermite finite elements | rest = Comput. Methods Appl. Mech. Engr., '''199''':3297-3304 }} | + | [2] {{reference-paper |author = Holdeman, J. T. and Kim, J.W. |year = 2010 | title = Computation of incompressible thermal flows using Hermite finite elements | rest = Comput. Methods Appl. Mech. Engr., '''199''': 3297-3304 }} |
| - | [3] {{reference-paper |author = Melosh, R. J. | year = 1963 | title = Basis of derivation of matricies for the direct stifness method | rest = J. A. I. A. A., '''1''':1631-1637 }} | + | [3] {{reference-paper |author = Melosh, R. J. | year = 1963 | title = Basis of derivation of matricies for the direct stifness method | rest = J.A.I.A.A., '''1''': 1631-1637 }} |
| - | [4] {{reference-book | author = Zienkiewicz, O. C. | year = 1971 | title = The | + | [4] {{reference-book | author = Zienkiewicz, O. C. | year = 1971 | title = The Finite Element Method in Engineering Science | rest = McGraw-Hill, London}} |
Revision as of 22:44, 9 July 2011
Lid-driven cavity using pressure-free velocity formulation
This sample code uses four-node simple-cubic finite elements and simple iteration.
Theory
The incompressible Navier-Stokes equation is a differential algebraic equation, having the inconvenient feature that there is no explicit mechanism for advancing the pressure in time. Consequently, much effort has been expended to eliminate the pressure from all or part of the computational process. We show a simple, natural way of doing this.
The incompressible Navier-Stokes equation is composite, the sum of two orthogonal equations,
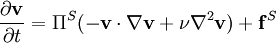 ,
,
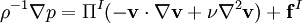 ,
,
where 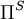 and
and 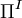 are solenoidal and irrotational projection operators satisfying
are solenoidal and irrotational projection operators satisfying 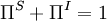 and
and
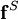 and
and 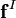 are the nonconservative and conservative parts of the body force. This result follows from the Helmholtz Theorem . The first equation is a pressureless governing equation for the velocity, while the second equation for the pressure is a functional of the velocity and is related to the pressure Poisson equation. The explicit functional forms of the projection operator in 2D and 3D are found from the Helmholtz Theorem, showing that these are integro-differential equations, and not particularly convenient for numerical computation.
are the nonconservative and conservative parts of the body force. This result follows from the Helmholtz Theorem . The first equation is a pressureless governing equation for the velocity, while the second equation for the pressure is a functional of the velocity and is related to the pressure Poisson equation. The explicit functional forms of the projection operator in 2D and 3D are found from the Helmholtz Theorem, showing that these are integro-differential equations, and not particularly convenient for numerical computation.
Equivalent weak or variational forms of the equations, proved to produce the same velocity solution as the Navier-Stokes equation are
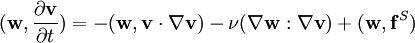 ,
,
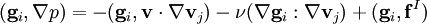 ,
,
for divergence-free test functions 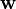 and irrotational test functions
and irrotational test functions 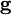 satisfying appropriate boundary conditions. Here, the projections are accomplished by the orthogonality of the solenoidal and irrotational function spaces. The discrete form of this is emminently suited to finite element computation of divergence-free flow.
satisfying appropriate boundary conditions. Here, the projections are accomplished by the orthogonality of the solenoidal and irrotational function spaces. The discrete form of this is emminently suited to finite element computation of divergence-free flow.
In the discrete case, it is desirable to choose basis functions for the velocity which reflect the essential feature of incompressible flow — the velocity elements must be divergence-free. While the velocity is the variable of interest, the existence of the stream function or vector potential is necessary by the Helmholtz Theorem. Further, to determine fluid flow in the absence of a pressure gradient, one can specify the difference of stream function values across a 2D channel, or the line integral of the tangential component of the vector potential around the channel in 3D, the flow being given by Stokes' Theorem. This leads naturally to the use of Hermite stream function (in 2D) or velocity potential elements (in 3D).
Involving, as it does, both stream function and velocity degrees-of-freedom, the method might be called a velocity-stream function or stream function-velocity method.
We now restrict discussion to 2D continuous Hermite finite elements which have at least first-derivative degrees-of-freedom. With this, one can draw a large number of candidate triangular and rectangular elements from the plate-bending literature. These elements have derivatives as components of the gradient. In 2D, the gradient and curl of a scalar are clearly orthogonal, given by the expressions,
Adopting continuous plate-bending elements, interchanging the derivative degrees-of-freedom and changing the sign of the appropriate one gives many families of stream function elements.
Taking the curl of the scalar stream function elements gives divergence-free velocity elements [1][2]. The requirement that the stream function elements be continuous assures that the normal component of the velocity is continuous across element interfaces, all that is necessary for vanishing divergence on these interfaces.
Boundary conditions are simple to apply. The stream function is constant on no-flow surfaces, with no-slip velocity conditions on surfaces. Stream function differences across open channels determine the flow. No boundary conditions are necessary on open boundaries [1], though consistent values may be used with some problems. These are all Dirichlet conditions.
The algebraic equations to be solved are simple to set up, but of course are non-linear, requiring iteration of the linearized equations.
The finite elements we will use here are apparently due to Melosh [3], but can also be found in Zienkiewitz [4]. These simple cubic-complete elements have three degrees-of-freedom at each of the four nodes. In the sample code we use this Hermite element for the pressure, and the modified form obtained by interchanging derivatives and the sign of one of them (though a simple bilinear element could be used for the pressure as well). The degrees-of-freedom are the pressure and pressure gardient, and the stream function and components of the solenoidal velocity for the modified element. The normal component of the velocity is continuous at element interfaces as is required, but the tangential velocity component may not be continuous.
The code implementing the lid-driven cavity problem is written for Matlab. The script below is problem-specific, and calls problem-independent functions to evaluate the element diffusion and convection matricies and evaluate the pressure from the resulting velocity field. These three functions accept general quadrilateral elements with straight sides as well as the rectangular elements used here. Other functions are a GMRES iterative solver using ILU preconditioning and incorporating the essential boundary conditions, and a function to produce non-uniform nodal spacing for the problem mesh.
This "educational code" is a simplified version of the code used in [1]. The user interface is the code itself. The user can experiment with changing the mesh, the Reynolds number, and the number of nonlinear iterations performed, as well as the relaxation factor. There are suggestions in the code regarding near-optimum choices for this factor as a function of Reynolds number. These values are given in the paper as well. For larger Reynolds numbers, a smaller relaxation factor speeds up convergence by smoothing the velocity factor 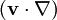 in the convection term, but will impede convergence if made too small.
in the convection term, but will impede convergence if made too small.
The output consists of graphic plots of contour levels of the stream function and the pressure levels.
This simplified version for this Wiki resulted from removal of computation of the vorticity, a restart capability, area weighting for the error, and production of publication-quality plots from one of the research codes used with the paper.
Lid-driven cavity Matlab script
%LDCW LID-DRIVEN CAVITY
% Finite element solution of the 2D Navier-Stokes equation using 4-node, 12 DOF,
% (3-DOF/node), simple-cubic-derived rectangular Hermite basis for
% the Lid-Driven Cavity problem.
%
% This could also be characterized as a VELOCITY-STREAM FUNCTION or
% STREAM FUNCTION-VELOCITY method.
%
% Reference: "A Hermite finite element method for incompressible fluid flow",
% Int. J. Numer. Meth. Fluids, 64, P376-408 (2010).
%
% Simplified Wiki version
% The rectangular problem domain is defined between Cartesian
% coordinates Xmin & Xmax and Ymin & Ymax.
% The computational grid has NumEx elements in the x-direction
% and NumEy elements in the y-direction.
% The nodes and elements are numbered column-wise from the
% upper left corner to the lower right corner.
%
%This script calls the user-defined functions:
% regrade - to regrade the mesh
% DMatW - to evaluate element diffusion matrix
% CMatW - to evaluate element convection matrix
% GetPresW - to evaluate the pressure
% ilu_gmres_with_EBC - to solve the system with essential/Dirichlet BCs
%
% Jonas Holdeman August 2007, revised June 2011
clear all;
disp('Lid-driven cavity');
disp(' Four-node, 12 DOF, simple-cubic stream function basis.');
% -------------------------------------------------------------
nd = 3; nd2=nd*nd; % Number of DOF per node - do not change!!
% -------------------------------------------------------------
ETstart=clock;
% Parameters for GMRES solver
GMRES.Tolerance=1.e-14;
GMRES.MaxIterates=15;
GMRES.MaxRestarts=6;
% Optimal relaxation parameters for given Reynolds number
% (see IJNMF reference)
% Re 100 1000 3200 5000 7500 10000 12500
% RelxFac: 1.04 1.11 .860 .830 .780 .778 .730
% ExpCR1 1.488 .524 .192 .0378 -- -- --
% ExpCRO 1.624 .596 .390 .331 .243 .163 .133
% CritFac: 1.82 1.49 1.14 1.027 .942 .877 .804
% Define the problem geometry, set mesh bounds:
Xmin = 0.0; Xmax = 1.0; Ymin = 0.0; Ymax = 1.0;
% Set mesh grading parameters (set to 1 if no grading).
% See below for explanation of use of parameters.
xgrd = .75; ygrd=.75; % (xgrd = 1, ygrd=1 for uniform mesh)
% Set " RefineBoundary=1 " for additional refinement at boundary,
% i.e., split first element along boundary into two.
RefineBoundary=1;
% DEFINE THE MESH
% Set number of elements in each direction
NumEx = 18; NumEy = NumEx;
% PLEASE CHANGE OR SET NUMBER OF ELEMENTS TO CHANGE/SET NUMBER OF NODES!
NumNx=NumEx+1; NumNy=NumEy+1;
% Define problem parameters:
% Lid velocity
Vlid=1.;
% Reynolds number
Re=1000.;
% factor for under/over-relaxation starting at iteration RelxStrt
RelxFac = 1.; %
% Number of nonlinear iterations
MaxNLit=20; %
%--------------------------------------------------------
% Viscosity for specified Reynolds number
nu=Vlid*(Xmax-Xmin)/Re;
% Grade the mesh spacing if desired, call regrade(x,agrd,e).
% if e=0: refine both sides, 1: refine upper, 2: refine lower
% if agrd=xgrd|ygrd is the parameter which controls grading, then
% if agrd=1 then leave array unaltered.
% if agrd<1 then refine (make finer) towards the ends
% if agrd>1 then refine (make finer) towards the center.
%
% Generate equally-spaced nodal coordinates and refine if desired.
if (RefineBoundary==1)
XNc=linspace(Xmin,Xmax,NumNx-2);
XNc=[XNc(1),(.62*XNc(1)+.38*XNc(2)),XNc(2:end-1),(.38*XNc(end-1)+.62*XNc(end)),XNc(end)];
YNc=linspace(Ymax,Ymin,NumNy-2);
YNc=[YNc(1),(.62*YNc(1)+.38*YNc(2)),YNc(2:end-1),(.38*YNc(end-1)+.62*YNc(end)),YNc(end)];
else
XNc=linspace(Xmin,Xmax,NumNx);
YNc=linspace(Ymax,Ymin,NumNy);
end
if xgrd ~= 1 XNc=regrade(XNc,xgrd,0); end; % Refine mesh if desired
if ygrd ~= 1 YNc=regrade(YNc,ygrd,0); end;
[Xgrid,Ygrid]=meshgrid(XNc,YNc);% Generate the x- and y-coordinate meshes.
% Allocate storage for fields
psi0=zeros(NumNy,NumNx);
u0=zeros(NumNy,NumNx);
v0=zeros(NumNy,NumNx);
%--------------------Begin grid plot-----------------------
% ********************** FIGURE 1 *************************
% Plot the grid
figure(1);
clf;
orient portrait; orient tall;
subplot(2,2,1);
hold on;
plot([Xmax;Xmin],[YNc;YNc],'k');
plot([XNc;XNc],[Ymax;Ymin],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal;
axis image;
title([num2str(NumNx) 'x' num2str(NumNy) ...
' node mesh for Lid-driven cavity']);
pause(.1);
%-------------- End plotting Figure 1 ----------------------
%Contour levels, Ghia, Ghia & Shin, Re=100, 400, 1000, 3200, ...
clGGS=[-.1175,-.1150,-.11,-.1,-.09,-.07,-.05,-.03,-.01,-1.e-4,-1.e-5,-1.e-7,-1.e-10,...
1.e-8,1.e-7,1.e-6,1.e-5,5.e-5,1.e-4,2.5e-4,5.e-4,1.e-3,1.5e-3,3.e-3];
CL=clGGS; % Select contour level option
if (Vlid<0) CL=-CL; end
NumNod=NumNx*NumNy; % total number of nodes
MaxDof=nd*NumNod; % maximum number of degrees of freedom
EBC.Mxdof=nd*NumNod; % maximum number of degrees of freedom
nn2nft=zeros(2,NumNod); % node number -> nf & nt
NodNdx=zeros(2,NumNod);
% Generate lists of active nodal indices, freedom number & type
ni=0; nf=-nd+1; nt=1; % ________
for nx=1:NumNx % | |
for ny=1:NumNy % | |
ni=ni+1; % |________|
NodNdx(:,ni)=[nx;ny];
nf=nf+nd; % all nodes have 3 dofs
nn2nft(:,ni)=[nf;nt]; % dof number & type (all nodes type 1)
end;
end;
%NumNod=ni; % total number of nodes
nf2nnt=zeros(2,MaxDof); % (node, type) associated with dof
ndof=0; dd=[1:nd];
for n=1:NumNod
for k=1:nd
nf2nnt(:,ndof+k)=[n;k];
end
ndof=ndof+nd;
end
NumEl=NumEx*NumEy;
% Generate element connectivity, from upper left to lower right.
Elcon=zeros(4,NumEl);
ne=0; LY=NumNy;
for nx=1:NumEx
for ny=1:NumEy
ne=ne+1;
Elcon(1,ne)=1+ny+(nx-1)*LY;
Elcon(2,ne)=1+ny+nx*LY;
Elcon(3,ne)=1+(ny-1)+nx*LY;
Elcon(4,ne)=1+(ny-1)+(nx-1)*LY;
end % loop on ny
end % loop on nx
% Begin essential boundary conditions, allocate space
MaxEBC = nd*2*(NumNx+NumNy-2);
EBC.dof=zeros(MaxEBC,1); % Degree-of-freedom index
EBC.typ=zeros(MaxEBC,1); % Dof type (1,2,3)
EBC.val=zeros(MaxEBC,1); % Dof value
X1=XNc(2); X2=XNc(NumNx-1);
nc=0;
for nf=1:MaxDof
ni=nf2nnt(1,nf);
nx=NodNdx(1,ni);
ny=NodNdx(2,ni);
x=XNc(nx);
y=YNc(ny);
if(x==Xmin | x==Xmax | y==Ymin)
nt=nf2nnt(2,nf);
switch nt;
case {1, 2, 3}
nc=nc+1; EBC.typ(nc)=nt; EBC.dof(nc)=nf; EBC.val(nc)=0; % psi, u, v
end % switch (type)
elseif (y==Ymax)
nt=nf2nnt(2,nf);
switch nt;
case {1, 3}
nc=nc+1; EBC.typ(nc)=nt; EBC.dof(nc)=nf; EBC.val(nc)=0; % psi, v
case 2
nc=nc+1; EBC.typ(nc)=nt; EBC.dof(nc)=nf; EBC.val(nc)=Vlid; % u
end % switch (type)
end % if (boundary)
end % for nf
EBC.num=nc;
if (size(EBC.typ,1)>nc) % Truncate arrays if necessary
EBC.typ=EBC.typ(1:nc);
EBC.dof=EBC.dof(1:nc);
EBC.val=EBC.val(1:nc);
end % End ESSENTIAL (Dirichlet) boundary conditions
% partion out essential (Dirichlet) dofs
p_vec = [1:EBC.Mxdof]'; % List of all dofs
EBC.p_vec_undo = zeros(1,EBC.Mxdof);
% form a list of non-diri dofs
EBC.ndro = p_vec(~ismember(p_vec, EBC.dof)); % list of non-diri dofs
% calculate p_vec_undo to restore Q to the original dof ordering
EBC.p_vec_undo([EBC.ndro;EBC.dof]) = [1:EBC.Mxdof]; %p_vec';
Q=zeros(MaxDof,1); % Allocate space for solution (dof) vector
% Initialize fields to boundary conditions
for k=1:EBC.num
Q(EBC.dof(k))=EBC.val(k);
end;
errpsi=zeros(NumNy,NumNx); % error correct for iteration
MxNL=max(1,MaxNLit);
np0=zeros(1,MxNL); % Arrays for convergence info
nv0=zeros(1,MxNL);
Qs=[];
Dmat = spalloc(MaxDof,MaxDof,36*MaxDof); % to save the diffusion matrix
Vdof=zeros(nd,4);
Xe=zeros(2,4); % coordinates of element corners
NLitr=0; ND=1:nd;
while (NLitr<MaxNLit), NLitr=NLitr+1; % <<< BEGIN NONLINEAR ITERATION
tclock=clock; % Start assembly time <<<<<<<<<
% Generate and assemble element matrices
Mat=spalloc(MaxDof,MaxDof,36*MaxDof);
RHS=spalloc(MaxDof,1,MaxDof);
%RHS = zeros(MaxDof,1);
Emat=zeros(1,16*nd2); % Values 144=4*4*(nd*nd)
% BEGIN GLOBAL MATRIX ASSEMBLY
for ne=1:NumEl
for k=1:4
ki=NodNdx(:,Elcon(k,ne));
Xe(:,k)=[XNc(ki(1));YNc(ki(2))];
end
if NLitr == 1
% Fluid element diffusion matrix, save on first iteration
[DEmat,Rndx,Cndx] = DMatW(Xe,Elcon(:,ne),nn2nft);
Dmat=Dmat+sparse(Rndx,Cndx,DEmat,MaxDof,MaxDof); % Global diffusion mat
end
if (NLitr>1)
% Get stream function and velocities
for n=1:4
Vdof(ND,n)=Q((nn2nft(1,Elcon(n,ne))-1)+ND); % Loop over local element nodes
end
% Fluid element convection matrix, first iteration uses Stokes equation.
[Emat,Rndx,Cndx] = CMatW(Xe,Elcon(:,ne),nn2nft,Vdof);
Mat=Mat+sparse(Rndx,Cndx,-Emat,MaxDof,MaxDof); % Global convection assembly
end
end; % loop ne over elements
% END GLOBAL MATRIX ASSEMBLY
Mat = Mat -nu*Dmat; % Add in cached/saved global diffusion matrix
disp(['(' num2str(NLitr) ') Matrix assembly complete, elapsed time = '...
num2str(etime(clock,tclock)) ' sec']); % Assembly time <<<<<<<<<<<
pause(1);
Q0 = Q; % Save dof values
% Solve system
tclock=clock; %disp('start solution'); % Start solution time <<<<<<<<<<<<<<
RHSr=RHS(EBC.ndro)-Mat(EBC.ndro,EBC.dof)*EBC.val;
Matr=Mat(EBC.ndro,EBC.ndro);
Qs=Q(EBC.ndro);
Qr=ilu_gmres_with_EBC(Matr,RHSr,[],GMRES,Qs);
Q=[Qr;EBC.val]; % Augment active dofs with esential (Dirichlet) dofs
Q=Q(EBC.p_vec_undo); % Restore natural order
stime=etime(clock,tclock); % Solution time <<<<<<<<<<<<<<
% ****** APPLY RELAXATION FACTOR *********************
if(NLitr>1) Q=RelxFac*Q+(1-RelxFac)*Q0; end
% ****************************************************
% Compute change and copy dofs to field arrays
dsqp=0; dsqv=0;
for k=1:MaxDof
ni=nf2nnt(1,k); nx=NodNdx(1,ni); ny=NodNdx(2,ni);
switch nf2nnt(2,k) % switch on dof type
case 1
dsqp=dsqp+(Q(k)-Q0(k))^2; psi0(ny,nx)=Q(k);
errpsi(ny,nx)=Q0(k)-Q(k);
case 2
dsqv=dsqv+(Q(k)-Q0(k))^2; u0(ny,nx)=Q(k);
case 3
dsqv=dsqv+(Q(k)-Q0(k))^2; v0(ny,nx)=Q(k);
end % switch on dof type
end % for
np0(NLitr)=sqrt(dsqp);
nv0(NLitr)=sqrt(dsqv);
if (np0(NLitr)<=1e-15|nv0(NLitr)<=1e-15)
MaxNLit=NLitr; np0=np0(1:MaxNLit); nv0=nv0(1:MaxNLit); end;
disp(['(' num2str(NLitr) ') Solution time for linear system = '...
num2str(etime(clock,tclock)) ' sec']); % Solution time <<<<<<<<<<<<
%---------- Begin plot of intermediate results ----------
% ********************** FIGURE 2 *************************
figure(1);
% Stream function (intermediate)
subplot(2,2,3);
contour(Xgrid,Ygrid,psi0,8,'k'); % Plot contours (trajectories)
axis([Xmin,Xmax,Ymin,Ymax]);
title(['Lid-driven cavity, Re=' num2str(Re)]);
axis equal; axis image;
% Plot convergence info
subplot(2,2,2);
semilogy(1:NLitr,nv0(1:NLitr),'k-+',1:NLitr,np0(1:NLitr),'k-o');
xlabel('Nonlinear iteration number');
ylabel('Nonlinear correction');
axis square;
title(['Iteration conv., Re=' num2str(Re)]);
legend('U','Psi');
% Plot nonlinear iteration correction contours
subplot(2,2,4);
contour(Xgrid,Ygrid,errpsi,8,'k'); % Plot contours (trajectories)
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Iteration correction']);
pause(1);
% ********************** END FIGURE 2 *************************
%---------- End plot of intermediate results ---------
if (nv0(NLitr)<1e-15) break; end % Terminate iteration if non-significant
end; % <<< (while) END NONLINEAR ITERATION
format short g;
disp('Convergence results by iteration: velocity, stream function');
disp(['nv0: ' num2str(nv0)]); disp(['np0: ' num2str(np0)]);
% >>>>>>>>>>>>>> BEGIN PRESSURE RECOVERY <<<<<<<<<<<<<<<<<<
% Essential pressure boundary condition
% Index of node to apply pressure BC, value at node
PBCnx=fix((NumNx+1)/2); % Apply at center of mesh
PBCny=fix((NumNy+1)/2);
PBCnod=0;
for k=1:NumNod
if (NodNdx(1,k)==PBCnx & NodNdx(2,k)==PBCny) PBCnod=k; break; end
end
if (PBCnod==0) error('Pressure BC node not found');
else
EBCp.nodn = [PBCnod]; % Pressure BC node number
EBCp.val = [0]; % set P = 0.
end
% Cubic pressure
[P,Px,Py] = GetPresW(NumNod,NodNdx,Elcon,nn2nft,Xgrid,Ygrid,Q,EBCp,nu);
% ******************** END PRESSURE RECOVERY *********************
% ********************** CONTINUE FIGURE 1 *************************
figure(1);
% Stream function (final)
subplot(2,2,3);
[CT,hn]=contour(Xgrid,Ygrid,psi0,CL,'k'); % Plot contours (trajectories)
clabel(CT,hn,CL([1,3,5,7,9,10,11,19,23]));
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Stream lines, ' num2str(NumNx) 'x' num2str(NumNy) ...
' mesh, Re=' num2str(Re)]);
% Plot pressure contours (final)
subplot(2,2,4);
CPL=[-.002,0,.02,.05,.07,.09,.11,.12,.17,.3];
[CT,hn]=contour(Xgrid,Ygrid,P,CPL,'k'); % Plot pressure contours
clabel(CT,hn,CPL([3,5,7,10]));
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Simple cubic pressure contours, Re=' num2str(Re)]);
% ********************* END FIGURE 1 *************************
disp(['Total elapsed time = '...
num2str(etime(clock,ETstart)/60) ' min']); % Elapsed time from start <<<
Diffusion matrix for pressure-free velocity method (DMatW.m)
Convection matrix for pressure-free velocity method (CMatW.m)
Consistent pressure for pressure-free velocity method (GetPresW.m)
GMRES solver with ILU preconditioning and Essential BC (ilu_gmres_with_EBC.m)
Grade node spacing (regrade.m)
references
[1] Holdeman, J. T. (2010), "A Hermite finite element method for incompressible fluid flow", Int. J. Numer. Meth. Fluids, 64: 376-408.
[2] Holdeman, J. T. and Kim, J.W. (2010), "Computation of incompressible thermal flows using Hermite finite elements", Comput. Methods Appl. Mech. Engr., 199: 3297-3304.
[3] Melosh, R. J. (1963), "Basis of derivation of matricies for the direct stifness method", J.A.I.A.A., 1: 1631-1637.
[4] Zienkiewicz, O. C. (1971), The Finite Element Method in Engineering Science, McGraw-Hill, London.

![\nabla\phi = \left[\frac{\partial \phi}{\partial x},\,\frac{\partial \phi}{\partial y}\right]^T, \quad
\nabla\times\phi = \left[\frac{\partial \phi}{\partial y},\,-\frac{\partial \phi}{\partial x}\right]^T.](/W/images/math/8/a/5/8a58150cd07872905de0f26ea5212055.png)