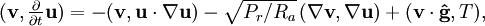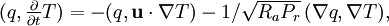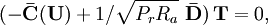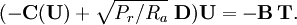Code: Thermal cavity using pressure-free velocity form
From CFD-Wiki
Thermal cavity using pressure-free velocity formulation
This sample code uses four-node quartic Hermite finite elements for velocity and simple-cubic Hermite elements for the temperature and pressure, and uses simple and iteration.
Theory
The incompressible Navier-Stokes equation is a differential algebraic equation, having the inconvenient feature that there is no explicit mechanism for advancing the pressure in time. Consequently, much effort has been expended to eliminate the pressure from all or part of the computational process. We show a simple, natural way of doing this.
The incompressible Navier-Stokes equation is composite, the sum of two orthogonal equations,
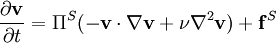 ,
,
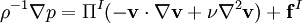 ,
,
where 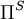 and
and 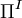 are solenoidal and irrotational projection operators satisfying
are solenoidal and irrotational projection operators satisfying 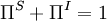 and
and
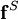 and
and 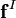 are the nonconservative and conservative parts of the body force. This result follows from the Helmholtz Theorem . The first equation is a pressureless governing equation for the velocity, while the second equation for the pressure is a functional of the velocity and is related to the pressure Poisson equation. The explicit functional forms of the projection operator in 2D and 3D are found from the Helmholtz Theorem, showing that these are integro-differential equations, and not particularly convenient for numerical computation.
are the nonconservative and conservative parts of the body force. This result follows from the Helmholtz Theorem . The first equation is a pressureless governing equation for the velocity, while the second equation for the pressure is a functional of the velocity and is related to the pressure Poisson equation. The explicit functional forms of the projection operator in 2D and 3D are found from the Helmholtz Theorem, showing that these are integro-differential equations, and not particularly convenient for numerical computation.
Equivalent weak or variational forms of the equations, proved to produce the same velocity solution as the Navier-Stokes equation are
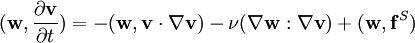 ,
,
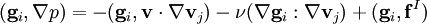 ,
,
for divergence-free test functions 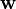 and irrotational test functions
and irrotational test functions 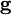 satisfying appropriate boundary conditions. Here, the projections are accomplished by the orthogonality of the solenoidal and irrotational function spaces. The discrete form of this is emminently suited to finite element computation of divergence-free flow.
satisfying appropriate boundary conditions. Here, the projections are accomplished by the orthogonality of the solenoidal and irrotational function spaces. The discrete form of this is emminently suited to finite element computation of divergence-free flow.
In the discrete case, it is desirable to choose basis functions for the velocity which reflect the essential feature of incompressible flow — the velocity elements must be divergence-free. While the velocity is the variable of interest, the existence of the stream function or vector potential is necessary by the Helmholtz Theorem. Further, to determine fluid flow in the absence of a pressure gradient, one can specify the difference of stream function values across a 2D channel, or the line integral of the tangential component of the vector potential around the channel in 3D, the flow being given by Stokes' Theorem. This leads naturally to the use of Hermite stream function (in 2D) or velocity potential elements (in 3D).
Involving, as it does, both stream function and velocity degrees-of-freedom, the method might be called a velocity-stream function or stream function-velocity method.
We now restrict discussion to 2D continuous Hermite finite elements which have at least first-derivative degrees-of-freedom. With this, one can draw a large number of candidate triangular and rectangular elements from the plate-bending literature. These elements have derivatives as components of the gradient. In 2D, the gradient and curl of a scalar are clearly orthogonal, given by the expressions,
Adopting continuous plate-bending elements, interchanging the derivative degrees-of-freedom and changing the sign of the appropriate one gives many families of stream function elements.
Taking the curl of the scalar stream function elements gives divergence-free velocity elements [3][4]. The requirement that the stream function elements be continuous assures that the normal component of the velocity is continuous across element interfaces, all that is necessary for vanishing divergence on these interfaces.
Boundary conditions are simple to apply. The stream function is constant on no-flow surfaces, with no-slip velocity conditions on surfaces. Stream function differences across open channels determine the flow. No boundary conditions are necessary on open boundaries [3], though consistent values may be used with some problems. These are all Dirichlet conditions.
The algebraic equations to be solved are simple to set up, but of course are non-linear, requiring iteration of the linearized equations.
For the thermal cavity, an energy equation expressed in terms of the temperature is introduced, and when the temperature-dependent density changes are small, a temperature-dependent buoyancy force 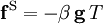 is introduced into the velocity equation. One nondimensional form is,
is introduced into the velocity equation. One nondimensional form is,
where Ra is the Rayleigh number and Pr is the Prandtl number. The velocity and temperature equations are coupled through the buoyancy force. In the following code we choose to split the equations. Instead of solving the coupled equations, which involves a larger matrix, we sequentially solve the steady nonlinear algebraic equations,
This results in smaller sets to be solved, but precludes using Newton's method to speed convergence. The solution of this pair is iterated until convegence.
The finite elements we will use here are a modified form of one due to Gopapacharyulu [1][2] and Watkins [5][6]. These quartic-complete elements have 24 degrees-of-freedom, six degrees-of-freedom at each of the four nodes, and have continuous first derivatives. In the sample code the modified form of the Hermite element was obtained by interchanging first derivatives and the sign of one of them. The degrees-of-freedom of the modified element are the stream function, two components of the solenoidal velocity, and three second derivatives of the stream function. The components of the velocity element, obtained by taking the curl of the stream function element, are continuous at element interfaces. Simple-cubic Hermite elements with three degrees-of-freedom are used for the temperature and pressure, though a simple bilinear element could be used for pressure.
The code implementing the thermal cavity problem is written for Matlab. The script below is problem-specific, and calls problem-independent functions to evaluate the velocity and thermal element diffusion and convection matricies, the buoyancy matrix, and to evaluate the pressure from the resulting velocity field. These six functions accept general convex quadrilateral elements with straight sides, as well as the rectangular elements used here. Other functions are a GMRES iterative solver using ILU preconditioning and incorporating the essential boundary conditions, and a function to produce non-uniform nodal spacing for the problem mesh.
This "educational code" is a simplified version of code used in [4]. The user interface is the code itself. The user can experiment with changing the mesh, the Rayleigh number, and the number of nonlinear iterations performed, as well as the relaxation factor, and there is an option for the nondimensional form of the temperature. There are suggestions in the code regarding near-optimum choices for this factor as a function of Rayleigh number. For larger Rayleigh numbers, a smaller relaxation factor speeds up convergence by smoothing the velocity in the factor 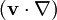 of the convection term, but will impede convergence if made too small.
of the convection term, but will impede convergence if made too small.
The output consists of graphic plots of contour levels of the stream function, temperature, velocity components, the pressure levels, and convergence rate.
This simplified version for this Wiki resulted from removal of computation of the vorticity field, a restart capability, comparison with published data, and production of publication-quality plots from the research code used with the paper. The vorticity at the nodes can be found, of course, from the second derivatives of the stream function. This code can be extended to fifth-order elements (and generalized bicubic elements), which use the same degrees-of-freedom, by simply replacing the functions evaluating the elements.
Thermal cavity Matlab script
%TC44SW THERMAL-DRIVEN CAVITY
%
% Finite element solution of the 2D Navier-Stokes equation for the
% bouyancy-driven thermal cavity problem using quartic Hermite elements
% and SEGMENTED SOLUTIONS (T-V split).
%
% This could be characterized as a VELOCITY-STREAM FUNCTION or
% STREAM FUNCTION-VELOCITY method.
%
% Reference: "Computation of incompressible thermal flows using Hermite finite
% elements", Comput. Methods Appl. Mech. Engrg, 199, P3297-3304 (2010).
%
% Simplified Wiki version
%
% The rectangular problem domain is defined between Cartesian
% coordinates Xmin & Xmax and Ymin & Ymax.
% The computational grid has NumNx nodes in the x-direction
% and NumNy nodes in the y-direction.
% The nodes and elements are numbered column-wise from the
% upper left corner to the lower right corner.
% Segmented version
%
%This script calls the user-defined functions:
% regrade - to regrade the mesh (optional)
% DMat4424W - to evaluate element velocity diffusion matrix
% CMat4424W - to evaluate element velocity convection matrix
% TDMat4424SW - to evaluate element thermal diffusion matrix
% TCMat4424SW - to evaluate element thermal convection matrix
% BMat4424SW - to evaluate element bouyancy matrix
% GetPres44243W - to evaluate the pressure
% ilu_gmres_with_EBC - to solve the system with essential/Dirichlet BCs
%
% Jonas Holdeman, December 2008 revised July 2011
clear all;
disp('Bouyancy-driven thermal cavity, T-V split');
disp(' Four-node, 24 dof quartic stream function basis, 12 dof cubic thermal basis.');
% ------------------ Fixed constants --------------------------
nV = 6; nV2=nV*nV; % Number velocity DOFs per node, DOFs squared.
nT = 3; nT2=nT*nT; % Number temperature DOFs per node, DOFs squared.
nD = nV+nT; nD2=nD*nD; % Total number of DOFs per node
% -------------------------------------------------------------
% Fixed parameters:
% Temperature on left, right side
TL=1; TR=0;
% Prandtl number
Pr=.71;
% Dimensionless equation form to be used
% Use EquationForm=1 for large Ra, EquationForm=0 for Ra->0
EquationForm=1; % (Choose 0 or 1)
ETstart=clock;
% Tolerance parameters for the GMRES iterative sparse solver
GMRESt.Tolerance=1.e-12; % For temperature
GMRESt.MaxIterates=20;
GMRESt.MaxRestarts=5;
GMRES.Tolerance=1.e-12;
GMRES.MaxIterates=20;
GMRES.MaxRestarts=5;
DropTol = []; % Use default drop tolerance in lui preconditioner
nn=[-1 -1; 1 -1; 1 1; -1 1]; % defines local nodal order
% Define the problem geometry:
Xmin = 0.0; Xmax = 1.0; Ymin = 0.0; Ymax = 1.0;
% Mesh grading parameters
xgrd = 1.0; ygrd=1.0; %
%xgrd = .75; ygrd=.75; %
% Set " RefineBoundary=1 " for additional refinement at boundary,
% i.e., split first element along each boundary into two.
RefineBoundary=0;
% DEFINE THE MESH:
% Number of elements in the x-direction
NumEx = 18;
% Number of elements in the y-direction
NumEy = 18;
NumEl = NumEx*NumEy;
% Number of nodes
NumNx = NumEx+1; NumNy = NumEy+1;
NumNod = NumNx*NumNy;
% --------------------------------------
% Suggested relaxation factors for steady flow
% Ra 10^3 10^4 10^5 10^6
% RelxFac .94 .67 .35 .04
% Rayleigh number Ra
Ra = 10^4;
% Relaxation factor ( <= 1 )
RelxFac=.67;
% Number of nonlinear iterations
MaxNLit=20;
%RA=Ra;
if (xgrd~=1 | ygrd~=1) meshsp='graded'; else meshsp='uniform'; end
disp(['Rayleigh number = ' num2str(Ra) ', ' num2str(NumEx) 'x' num2str(NumEy) ' element ' meshsp ' mesh' ]);
disp(['Maximum number of nonlinear iterations = ' num2str(MaxNLit)]);
disp(' ');
pause(1);
%--------------------------------------------------------
% Grade the mesh spacing if desired, call regrade(x,agrd,e).
% if e=0: refine both sides, 1: refine upper, 2: refine lower
% if agrd=xgrd|ygrd is the parameter which controls grading, then
% if agrd=1 then leave array unaltered.
% if agrd>1 then refine towards the ends
% if agrd<1 then refine towards the center.
%
% Generate equally-spaced nodal coordinates and refine if desired.
if (RefineBoundary==1)
XNc=linspace(Xmin,Xmax,NumNx-2);
XNc=[XNc(1),(.62*XNc(1)+.38*XNc(2)),XNc(2:end-1),(.38*XNc(end-1)+.62*XNc(end)),XNc(end)];
YNc=linspace(Ymax,Ymin,NumNy-2);
YNc=[YNc(1),.5*(YNc(1)+YNc(2)),YNc(2:end-1),(YNc(end-1)+YNc(end))/2.,YNc(end)];
else
XNc=linspace(Xmin,Xmax,NumNx);
YNc=linspace(Ymax,Ymin,NumNy);
end
if xgrd ~= 1 XNc=regrade(XNc,xgrd,0); end; % Refine mesh if desired
if ygrd ~= 1 YNc=regrade(YNc,ygrd,0); end;
[Xgrid,Ygrid]=meshgrid(XNc,YNc);% Generate the x- and y-coordinate meshes.
% Area-based nodal weights
wx=zeros(1,NumNx); wy=zeros(1,NumNy);
wx(1)=.5*(XNc(2)-XNc(1));
wx(2:NumNx-1)=.5*(XNc(3:NumNx)-XNc(1:NumNx-2));
wx(NumNx)=.5*(XNc(NumNx)-XNc(NumNx-1));
wy(1)=.5*(YNc(1)-YNc(2));
wy(2:NumNy-1)=.5*(YNc(1:NumNy-2)-YNc(3:NumNy));
wy(NumNy)=.5*(YNc(NumNy-1)-YNc(NumNy));
Wa=wy'*wx;
% Initial stream function and velocity, temperature & gradient fields
psi0=zeros(NumNy,NumNx);
u0=zeros(NumNy,NumNx);
v0=zeros(NumNy,NumNx);
pxx0=zeros(NumNy,NumNx);
pxy0=zeros(NumNy,NumNx);
pyy0=zeros(NumNy,NumNx);
T0=zeros(NumNy,NumNx);
Tx0=zeros(NumNy,NumNx);
Ty0=zeros(NumNy,NumNx);
%------------------Begin grid plot--------------------
% Plot the grid
figure(1);
clf;
orient portrait; orient tall;
subplot(2,2,2);
hold on;
plot([Xmax;Xmin],[YNc;YNc],'k');
plot([XNc;XNc],[Ymax;Ymin],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title([num2str(NumNx) 'x' num2str(NumNy) ' node mesh for thermal cavity']);
%-------------------End grid plot---------------------
MaxVdof=nV*NumNod;
MaxTdof=nT*NumNod;
MaxDof=MaxVdof+MaxTdof; % maximum number of degrees of freedom
VBC.Mxdof=MaxVdof; % maximum number V of degrees of freedom
TBC.Mxdof=MaxTdof; % maximum number of T degrees of freedom
nn2vft=zeros(2,NumNod); % node number -> nfv & nt
nn2tft=zeros(2,NumNod); % node number -> nft & nt
NodNdx=zeros(2,NumNod);
% Generate lists of active nodal indices, freedom number & type
ni=0; nt=1;
nfv=-nV+1; nft=-nT+1; % ________
for nx=1:NumNx % | |
for ny=1:NumNy % | |
ni=ni+1; % |________|
NodNdx(:,ni)=[nx;ny];
nfv=nfv+nV; % all V nodes have 6 dofs
nn2vft(:,ni)=[nfv;nt]; % dof number & type (all nodes type 1)
nft=nft+nT; % all T nodes have 3 dofs
nn2tft(:,ni)=[nft;nt]; % dof number & type (all nodes type 1)
end;
end;
%NumNod=ni; % total number of nodes
nvf2nnt=zeros(2,MaxVdof); % (node, type) associated with dof
ntf2nnt=zeros(2,MaxTdof); % (node, type) associated with dof
nfv=0; nft=0;
for n=1:NumNod
for k=1:nV
nvf2nnt(:,nfv+k)=[n;k];
end
nfv=nfv+nV;
for k=1:nT
ntf2nnt(:,nft+k)=[n;k];
end
nft=nft+nT;
end
% Generate element connectivity, from upper left to lower right.
Elcon=zeros(4,NumEl);
ne=0; LY=NumNy;
for nx=1:NumEx
for ny=1:NumEy
ne=ne+1;
Elcon(1,ne)=1+ny+(nx-1)*LY;
Elcon(2,ne)=1+ny+nx*LY;
Elcon(3,ne)=1+(ny-1)+nx*LY;
Elcon(4,ne)=1+(ny-1)+(nx-1)*LY;
end % loop on ny
end % loop on nx
% Begin ESSENTIAL (Dirichlet) V boundary conditions
MaxVBC=2*(5*NumNy+5*(NumNx-2)); % Allocate space for VBC
VBC.dof=zeros(MaxVBC,1); % Degree-of-freedom index
VBC.val=zeros(MaxVBC,1); % Dof value
nc=0;
for nf=1:MaxVdof
nt=nvf2nnt(2,nf); ni=nvf2nnt(1,nf);
nx=NodNdx(1,ni); ny=NodNdx(2,ni);
x=XNc(nx); y=YNc(ny);
if((x==Xmin | x==Xmax) & (y==Ymax | y==Ymin)) % corner
nc=nc+1; VBC.dof(nc)=nf; VBC.val(nc)=0; % psi, u, v, pxx, pxy, pyy
elseif(x==Xmin | x==Xmax) % left or right boundary
switch nt;
case {1, 2, 3, 5, 6}
nc=nc+1; VBC.dof(nc)=nf; VBC.val(nc)=0; % psi, u, v, pxy, pyy (pxx=-v_x free)
end % switch (type)
elseif (y==Ymax | y==Ymin) % top, bottom
switch nt
case {1, 2, 3, 4, 5}
nc=nc+1; VBC.dof(nc)=nf; VBC.val(nc)=0; % psi, u, v, pxx, pxy (pyy=u_y free)
end % switch (type)
end % if (boundary)
end % for nf
VBC.num=nc;
if (size(VBC.dof,1)>nc) % Truncate V arrays if necessary
VBC.dof=VBC.dof(1:nc);
VBC.val=VBC.val(1:nc);
end % truncate V
% End ESSENTIAL (Dirichlet) V boundary conditions
% Begin ESSENTIAL (Dirichlet) T boundary conditions
MaxTBC=2*(2*NumNy+(NumNx-2)); % Allocate space for TBC
TBC.dof=zeros(MaxTBC,1); % Degree-of-freedom index
TBC.val=zeros(MaxTBC,1); % Dof value
nc=0;
for nf=1:MaxTdof
nt=ntf2nnt(2,nf); ni=ntf2nnt(1,nf);
nx=NodNdx(1,ni); ny=NodNdx(2,ni);
x=XNc(nx); y=YNc(ny);
if(x==Xmin) % left boundary
switch nt;
case 1
nc=nc+1; TBC.dof(nc)=nf; TBC.val(nc)=TL; % T
case 3
nc=nc+1; TBC.dof(nc)=nf; TBC.val(nc)=0; % Ty
end % switch (type)
elseif (x==Xmax) % right boundary
switch nt;
case 1
nc=nc+1; TBC.dof(nc)=nf; TBC.val(nc)=TR; % T
case 3
nc=nc+1; TBC.dof(nc)=nf; TBC.val(nc)=0; % Ty
end % switch (type)
elseif (y==Ymax | y==Ymin) % top, bottom
switch nt
case 3
nc=nc+1; TBC.dof(nc)=nf; TBC.val(nc)=0; % Ty
end % switch (type)
end % if (boundary)
end % for nf
TBC.num=nc;
if (size(TBC.dof,1)>nc) % Truncate T arrays if necessary
TBC.dof=TBC.dof(1:nc);
TBC.val=TBC.val(1:nc);
end % truncate T
% End ESSENTIAL (Dirichlet) T boundary conditions
% Number active DOFs
ADOFs=MaxDof-VBC.num-TBC.num;
disp(['Number of active DOFs = ' num2str(ADOFs)]);
% partion out essential (Dirichlet) dofs
p_vec = [1:VBC.Mxdof]'; % List of all dofs
VBC.p_vec_undo = zeros(1,VBC.Mxdof);
% form a list of non-diri dofs
VBC.ndro = p_vec(~ismember(p_vec, VBC.dof)); % list of non-diri dofs
% calculate p_vec_undo to restore Q to the original dof ordering
VBC.p_vec_undo([VBC.ndro;VBC.dof]) = [1:VBC.Mxdof]; %p_vec';
p_vec = [1:TBC.Mxdof]'; % List of all dofs
TBC.p_vec_undo = zeros(1,TBC.Mxdof);
% form a list of non-diri dofs
TBC.ndro = p_vec(~ismember(p_vec, TBC.dof)); % list of non-diri dofs
% calculate p_vec_undo to restore Q to the original dof ordering
TBC.p_vec_undo([TBC.ndro;TBC.dof]) = [1:TBC.Mxdof]; %p_vec';
Qv=zeros(MaxVdof,1); % Allocate space for velocity solution (dof) vector
Qt=zeros(MaxTdof,1); % Allocate space for temperature solution (dof) vector
for k = 1:MaxTdof
nn=ntf2nnt(1,k);
nx=NodNdx(1,nn); ny=NodNdx(2,nn);
switch ntf2nnt(2,k) % switch on DOF type
case 1
Qt(k)=T0(ny,nx);
case 2
Qt(k)=Tx0(ny,nx);
case 3
Qt(k)=Ty0(ny,nx);
end; % switch (type)
end % loop over TDOFs
% Initialize fields to boundary conditions
KB=1:VBC.num;
Qv(VBC.dof(KB))=VBC.val(KB);
KB=1:TBC.num;
Qt(TBC.dof(KB))=TBC.val(KB);
errpsi=zeros(NumNy,NumNx); % error correct for iteration
MxNL=max(1,MaxNLit);
np0=zeros(1,MxNL); % Arrays for convergence info
nv0=zeros(1,MxNL);
nT0=zeros(1,MxNL);
if EquationForm==1
Ctd=1/sqrt(Ra*Pr); Cvd=Ctd*Pr; Cbf=1; % Coefficients for large Ra
else
Ctd=1; Cvd=Pr; Cbf=Pr*Ra; % Coefficients for small Ra
end
DMat = spalloc(MaxVdof,MaxVdof,54*MaxVdof); % to save the diffusion matrix
TDMat = spalloc(MaxTdof,MaxTdof,30*MaxTdof); % to save the thermal diffusion matrix
BMat = spalloc(MaxVdof,MaxTdof,18*MaxVdof); % to save the bouyancy matrix
MatV = []; % Velocity submatrix
MatT = []; % Temperature submatrix
Vdof=zeros(6,4);
Xe=zeros(2,4); % coordinates of element corners
NLitr=0;
NV=1:nV;
ItType=0; % Initialy simple iteration
while NLitr<MaxNLit, NLitr=NLitr+1; % <<< BEGIN NONLINEAR ITERATION
% Generate and assemble element matrices
CMat = spalloc(MaxVdof,MaxVdof,54*MaxVdof); % to save the fluid convection matrix
TCMat = spalloc(MaxTdof,MaxTdof,30*MaxTdof); % to save the thermal convection matrix
RHS=spalloc(MaxVdof,1,MaxVdof);
% Copy fields to dof vector
Qv0=Qv; Qt0=Qt;
tclock=clock; % Start assembly time <<<<<<<<<
for ne=1:NumEl % BEGIN GLOBAL MATRIX ASSEMBLY
for k=1:4
ki=NodNdx(:,Elcon(k,ne));
Xe(:,k)=[Xgrid(ki(2),ki(1));Ygrid(ki(2),ki(1))];
end
if NLitr == 1
% Fluid element diffusion matrix, save on first iteration
[DEmat,Rndx,Cndx] = DMat4424W(Xe,Elcon(:,ne),nn2vft); % Element fluid diffusion matrix
DMat = DMat + sparse(Rndx,Cndx,DEmat,MaxVdof,MaxVdof); % Global fluid diffusion matrix
[DEmat,Rndx,Cndx] = TDMat4424SW(Xe,Elcon(:,ne),nn2tft); % Element thermal diffusion matrix
TDMat = TDMat + sparse(Rndx,Cndx,DEmat,MaxTdof,MaxTdof); % Global thermal diffusion matrix
[DEmat,Rndx,Cndx] = BMat4424SW(Xe,Elcon(:,ne),nn2vft,nn2tft);
BMat = BMat + sparse(Rndx,Cndx,DEmat,MaxVdof,MaxTdof); % Global fluid bouyancy matrix
end
if (NLitr>1)
% First iteration uses Stokes equation.
% Get stream function and velocities for linearized Navier-Stokes
for n=1:4 % Loop over local nodes of element
Vdof(NV,n)=Qv((nn2vft(1,Elcon(n,ne))-1)+NV);
end
% Fluid element convection matrix
[CEmat,Rndx,Cndx] = CMat4424W(Xe,Elcon(:,ne),nn2vft,Vdof,0); % Element convection matrix
CMat = CMat + sparse(Rndx,Cndx,CEmat,MaxVdof,MaxVdof); % Global fluid convection assembly
% Thermal convection matrix
[CEmat,Rndx,Cndx] = TCMat4424SW(Xe,Elcon(:,ne),nn2tft,Vdof); % Element thermal convection matrix
TCMat = TCMat + sparse(Rndx,Cndx,CEmat,MaxTdof,MaxTdof); % Global thermal convection assembly
end; % NLitr>1
end; % END GLOBAL MATRIX ASSEMBLY
MatT = -Ctd*TDMat- TCMat;
MatV = -CMat -Cvd*DMat;
disp(['(' num2str(NLitr) ') Matrix assembly complete, elapsed time = '...
num2str(etime(clock,tclock)) ' sec']); % Assembly time <<<<<<<<<<<
pause(1);
% Solve system
tclock=clock; % Start solution time <<<<<<<<<<<<<<
RHSt=sparse(MaxTdof,1);
RHSt=RHSt(TBC.ndro)-MatT(TBC.ndro,TBC.dof)*TBC.val;
MatT=MatT(TBC.ndro,TBC.ndro);
Qs=Qt(TBC.ndro);
Qr=ilu_gmres_with_EBC(MatT,RHSt,[],GMRESt,Qs);
Qt=[Qr;TBC.val]; % Augment active dofs with esential (Dirichlet) dofs
Qt=Qt(TBC.p_vec_undo); % Restore natural order
RHS=RHS-Cbf*BMat*Qt;
RHS=RHS(VBC.ndro)-MatV(VBC.ndro,VBC.dof)*VBC.val;
MatV=MatV(VBC.ndro,VBC.ndro);
Qs=Qv(VBC.ndro);
Qr=ilu_gmres_with_EBC(MatV,RHS,[],GMRES,Qs,DropTol);
Qv=[Qr;VBC.val]; % Augment active dofs with esential (Dirichlet) dofs
Qv=Qv(VBC.p_vec_undo); % Restore natural order
% Copy dofs to field arrays, compute change
% --------------------------------------------
Qv=RelxFac*Qv+(1-RelxFac)*Qv0;
% --------------------------------------------
% Compute change and copy dofs to field arrays
dsqp=0; dsqv=0; dsqt=0;
for k=1:MaxVdof
ni=nvf2nnt(1,k);
nx=NodNdx(1,ni); ny=NodNdx(2,ni);
switch nvf2nnt(2,k) % switch on dof type
case 1
dsqp=dsqp+Wa(ny,nx)*(Qv(k)-Qv0(k))^2; psi0(ny,nx)=Qv(k);
errpsi(ny,nx)=Qv0(k)-Qv(k);
case 2
dsqv=dsqv+Wa(ny,nx)*(Qv(k)-Qv0(k))^2; u0(ny,nx)=Qv(k);
case 3
dsqv=dsqv+Wa(ny,nx)*(Qv(k)-Qv0(k))^2; v0(ny,nx)=Qv(k);
case 4
pxx0(ny,nx)=Qv(k);
case 5
pxy0(ny,nx)=Qv(k);
case 6
pyy0(ny,nx)=Qv(k);
end % switch on dof type
end % for
for k=1:MaxTdof
ni=ntf2nnt(1,k);
nx=NodNdx(1,ni); ny=NodNdx(2,ni);
switch ntf2nnt(2,k) % switch on dof type
case 1
dsqt=dsqt+Wa(ny,nx)*(Qt(k)-Qt0(k))^2; T0(ny,nx)=Qt(k);
case 2
Tx0(ny,nx)=Qt(k);
case 3
Ty0(ny,nx)=Qt(k);
end % switch on dof type
end % for
np0(NLitr)=sqrt(dsqp);
nv0(NLitr)=sqrt(dsqv);
nT0(NLitr)=sqrt(dsqt);
disp(['Solution time for linear system = '...
num2str(etime(clock,tclock)) ' sec, nv0=' num2str(nv0(NLitr))]); % Solution time <<<<<<<
if (np0(NLitr)<=1e-15|nv0(NLitr)<=1e-15|nT0(NLitr)<=1e-15)
MaxNLit=NLitr; np0=np0(1:MaxNLit); nv0=nv0(1:MaxNLit); nT0=nT0(1:MaxNLit); end;
%---------- Begin plot of intermediate results ----------
figure(2);
orient portrait;
orient tall;
% Stream function (intermediate)
subplot(2,2,1);
contour(Xgrid,Ygrid,psi0,10,'k'); % Plot contours (trajectories)
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Thermal cavity stream lines; Ra=' num2str(Ra)]);
% Temperature (intermediate)
subplot(2,2,3);
contour(Xgrid,Ygrid,T0,10,'k');
axis([Xmin,Xmax,Ymin,Ymax]);
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis equal; axis image;
title(['Thermal cavity isotherms, Ra=' num2str(Ra)]);
% Convergence
subplot(2,2,2);
semilogy(1:MaxNLit,nT0,'k-x',1:MaxNLit,nv0,'k-+',1:MaxNLit,np0,'k-o');
xlabel('Nonlinear iteration number');
ylabel('Nonlinear correction');
axis square;
title(['Iteration conv., Ra=' num2str(Ra)]);
legend('T','U','Psi');
% Error
subplot(2,2,4);
axis([Xmin,Xmax,Ymin,Ymax]);
contour(Xgrid,Ygrid,errpsi,8,'k'); % Plot contours (errors)
hold on;
pcolor(Xgrid,Ygrid,errpsi);
shading flat; % or interp
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis image;
title(['Iteration correction, psi']);
pause(1);
%---------- End plot of intermediate results ---------
end; % <<< END NONLINEAR ITERATION
format short g;
disp('Convergence results by iteration: temperature, velocity, stream function');
disp(['nT0: ' num2str(nT0)]); disp(['nv0: ' num2str(nv0)]); disp(['np0: ' num2str(np0)]);
% >>>>>>>>>>>>>> BEGIN PRESSURE RECOVERY <<<<<<<<<<<<<<<<<<
% Essential pressure boundary condition
% Index of node to apply pressure BC, value at node
PBCnx=fix((NumNx+1)/2); % Apply at center of mesh
PBCny=fix((NumNy+1)/2);
PBCnod=0;
for k=1:NumNod
if (NodNdx(1,k)==PBCnx & NodNdx(2,k)==PBCny) PBCnod=k; break; end
end
if (PBCnod==0) error('Pressure BC node not found');
else
EBCp.nodn = [PBCnod]; % Pressure BC node number
EBCp.val = [0]; % set P = 0.
end
% Cubic pressure
[P,Px,Py] = GetPres44243W(NumNod,NodNdx,Elcon,nn2vft,Xgrid,Ygrid,Qv,EBCp,Cvd);
%----------Plot of final result-------------
figure(1);
% Stream function (final)
subplot(2,2,1);
contour(Xgrid,Ygrid,psi0,10,'k'); % Plot contours (trajectories)
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Stream lines, Ra=' num2str(Ra)]);
% Temperature (final)
subplot(2,2,3);
contour(Xgrid,Ygrid,T0,10,'k');
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Isotherms, Ra=' num2str(Ra)]);...
% Plot pressure contours (final)
subplot(2,2,4);
contour(Xgrid,Ygrid,P,10,'k'); % Plot pressure contours
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['Pressure contours, Ra=' num2str(Ra)]);
% ************* FIGURE 2 ***********************
figure (2);
clf;
orient tall;
% U-velocity (final)
subplot(2,2,1);
contour(Xgrid,Ygrid,u0,10,'k'); % Plot vector field
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['U-velocity field']);...
% V-velocity (final)
subplot(2,2,3);
contour(Xgrid,Ygrid,v0,10,'k'); % Plot vector field
hold on;
plot([Xmin,Xmin,Xmax,Xmax,Xmin],[Ymax,Ymin,Ymin,Ymax,Ymax],'k');
hold off;
axis([Xmin,Xmax,Ymin,Ymax]);
axis equal; axis image;
title(['V-velocity field']);...
% Convergence
subplot(2,2,2);
semilogy(1:MaxNLit,nT0,'k-x',1:MaxNLit,nv0,'k-+',1:MaxNLit,np0,'k-o');
xlabel('Nonlinear iteration number');
ylabel('Nonlinear correction');
axis square;
title(['Iteration conv., Ra=' num2str(Ra)]);
legend('T','U','Psi');
subplot(2,2,4);
nc=fix((NumNy+1)/2);
plot(Xgrid(nc,:),T0(nc,:),'k-x');
title(['Centerline temperature']);...
% ----------- End final plot ------------
disp(['Total elapsed time = '...
num2str(etime(clock,ETstart)/60) ' min']); % Elapsed time from start <<<<<
return;
Program script for thermal cavity with pressure-free velocity method (TC44SW.m)
Modified-quartic velocity class for pressure-free velocity method (ELS4424r.m)
Simple-cubic pressure class for pressure-free velocity method (ELG3412r.m)
Velocity diffusion matrix for pressure-free velocity method (DMatW.m)
Velocity convection matrix for pressure-free velocity method (CMatW.m)
Thermal diffusion matrix for pressure-free velocity method (TDMatSW.m)
Thermal convection matrix for pressure-free velocity method (TCMatSW.m)
Buoyancy matrix for pressure-free velocity method (BMatSW.m)
Consistent pressure for pressure-free velocity method (GetPres3W.m)
Grade node spacing (regrade.m)
references
[1] Gopalacharyulu, S. (1973), "A higher order conforming rectangular plate element", Int. J. Numer. Meth. Fluids, 6: 305-308.
[2] Gopalacharyulu, S. (1976), "Author's reply to the discussion by Watkins", Int. J. Numer. Meth. Fluids, 10: 472-474.
[3] Holdeman, J. T. (2010), "A Hermite finite element method for incompressible fluid flow", Int. J. Numer. Meth. Fluids, 64: 376-408.
[4] Holdeman, J. T. and Kim, J.W. (2010), "Computation of incompressible thermal flows using Hermite finite elements", Comput. Methods Appl. Mech. Engr., 199: 3297-3304.
[5] Watkins, D. S. (1976), "A comment on Gopalacharyulu's 24 node element", Int. J. Numer. Meth. Fluids, 10: 471-472. }}
[6] Watkins, D. S. (1976), "On the construction of conforming rectangular plate elements", Int. J. Numer. Meth. Fluids, 10: 925-933. }}

![\nabla\phi = \left[\frac{\partial \phi}{\partial x},\,\frac{\partial \phi}{\partial y}\right]^T, \quad
\nabla\times\phi = \left[\frac{\partial \phi}{\partial y},\,-\frac{\partial \phi}{\partial x}\right]^T.](/W/images/math/8/a/5/8a58150cd07872905de0f26ea5212055.png)