Combustion
From CFD-Wiki
The power of Fire, or Flame, for instance, which we designate by some trivial chemical name, thereby hiding from ourselves the essential character of wonder that dwells in it as in all things, is with these old Northmen, Loke, a most swift subtle Demon of the brood of the Jötuns... From us too no Chemistry, if it had not Stupidity to help it, would hide that Flame is a wonder. What is Flame?
Carlyle on Heroes Odin and Scandinavian Mythology., [1].
What is combustion -- physics versus modelling
Combustion phenomena consist of many physical and chemical processes which exhibit a broad range of time and length scales. A mathematical description of combustion is not always trivial, although some analytical solutions exist for simple situations of laminar flame. Such analytical models are usually restricted to problems in zero or one-dimensional space.
Nomenclature
In a general manner, we shall try to stick to the official standards, the nomenclature for heat transfer, that may be found in an issue of Journal of Heat Transfer [2]
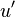 Turbulent integral RMS velocity
Turbulent integral RMS velocity
Fundamental Aspects
Main Specificities of Combustion Chemistry
Combustion can be split into two processes interacting with each other: thermal, and chemical.
The chemistry is highly exothermal (this is the reason of its use) but also highly temperature dependent, thus highly self-accelerating. In a simplified form, combustion can be represented by a single irreversible reaction involving 'a' fuel and 'an' oxidizer:
Although very simplified compared to real chemistry involving hundreds of species (and their individual transport properties) and elemental reactions, this rudimentary chemistry has been the cornerstone of combustion analysis and modelling.
The most widely used form for the rate of the above reaction is the Arrhénius law:
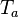 is the activation temperature, high in combustion, consistently with the temperature dependence.
This is where the high non-linearity in temperature is modelled. A is the pre-exponential constant. One of the interpretation of the Arrhénius law comes from gas kinetic theory: the number of molecules whose kinetic energy is larger than the minimum value allowing a collision to be energetic enough to trig a reaction is proportional to the exponential term introduced above divided by the square root of the temperature. This interpretation allows one to think that the temperature dependence of A is very weak compared to the exponential term. A is eventually considered as constant.
The reaction rate is also naturally proportional to the molecular density of each of the reactant. Nonetheless, the orders of reaction
is the activation temperature, high in combustion, consistently with the temperature dependence.
This is where the high non-linearity in temperature is modelled. A is the pre-exponential constant. One of the interpretation of the Arrhénius law comes from gas kinetic theory: the number of molecules whose kinetic energy is larger than the minimum value allowing a collision to be energetic enough to trig a reaction is proportional to the exponential term introduced above divided by the square root of the temperature. This interpretation allows one to think that the temperature dependence of A is very weak compared to the exponential term. A is eventually considered as constant.
The reaction rate is also naturally proportional to the molecular density of each of the reactant. Nonetheless, the orders of reaction 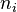 are different from the stoichiometric coefficients as the single-step reaction is global, not governed by collision for it represents hundreds of elementary reactions.
If one goes into the details, combustion chemistry is based on chain reactions, decomposed into three main steps: (i) generation (where radicals are created from the fresh mixture), (ii) branching (where products and new radicals appear from interaction of radicals with reactants), and (iii) termination (where radicals collide and turn into products). The branching step tends to accelerate the production of active radicals (autocatalytic). The impact is nevertheless small compared to the high non-linearity in temperature. This explains why single-step chemistry has been sufficient for most of the combustion modelling work up to now.
are different from the stoichiometric coefficients as the single-step reaction is global, not governed by collision for it represents hundreds of elementary reactions.
If one goes into the details, combustion chemistry is based on chain reactions, decomposed into three main steps: (i) generation (where radicals are created from the fresh mixture), (ii) branching (where products and new radicals appear from interaction of radicals with reactants), and (iii) termination (where radicals collide and turn into products). The branching step tends to accelerate the production of active radicals (autocatalytic). The impact is nevertheless small compared to the high non-linearity in temperature. This explains why single-step chemistry has been sufficient for most of the combustion modelling work up to now.
The fact that a flame is a very thin reaction zone separating, and making the transition between, a frozen mixture and an equilibrium is explained by the high temperature dependence of the reaction term, modelled by a large activation temperature, and a large heat release (the ratio of the burned and fresh gas temperatures is about 7 for typical hydrocarbon flames) leading to a sharp self-acceleration in a very narrow area. To evaluate the order of magnitude of the quantities, the terms in the exponential argument are normalized:
 is named the Zeldovitch number and
is named the Zeldovitch number and 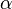 the heat release factor.
Here,
the heat release factor.
Here, 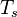 has been used instead of
has been used instead of 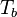 , the conventional notation for burned gas temperature (at final equilibrium).
, the conventional notation for burned gas temperature (at final equilibrium). 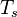 is actually
is actually 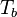 for a mixture at stoichiometry and when the system is adiabatic, i.e. this is the reference highest temperature that can be
obtained in the system.
for a mixture at stoichiometry and when the system is adiabatic, i.e. this is the reference highest temperature that can be
obtained in the system. 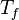 is the ambient temperature of the fresh gases. That said, typical value for
is the ambient temperature of the fresh gases. That said, typical value for  and
and 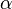 are 10 and 0.9, giving
a good taste of the level of non-linearity of the combustion process with respect to temperature.
Actually, the reaction rate is rewritten as:
are 10 and 0.9, giving
a good taste of the level of non-linearity of the combustion process with respect to temperature.
Actually, the reaction rate is rewritten as:
where the non-dimensionalized temperature is:
The non-linearity of the reaction rate is seen from the exponential term:
-
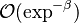 for
for 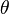 far from unity (in the fresh gas)
far from unity (in the fresh gas)
-
 for
for 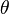 close to unity (in the reaction zone close to the burned gas whose temperature must be close to the adiabatic one
close to unity (in the reaction zone close to the burned gas whose temperature must be close to the adiabatic one 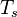 ), more exactly
), more exactly 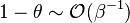
-
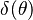 function. The figure, beside, illustrates how common values of
function. The figure, beside, illustrates how common values of  around 10 tend to make the reaction rate singular around
around 10 tend to make the reaction rate singular around 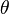 of unity. Two set of values are presented:
of unity. Two set of values are presented: 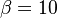 and
and 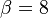 . The first magnitude is the representative value while the second one is a smoother one usually used to ease numerical simulations. In the same way, two values for the heat release
. The first magnitude is the representative value while the second one is a smoother one usually used to ease numerical simulations. In the same way, two values for the heat release 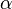 , 0.9 and 0.75, are explored. The heat release is seen to have a minor impact on the temperature non-linearity.
, 0.9 and 0.75, are explored. The heat release is seen to have a minor impact on the temperature non-linearity.
Transport Equations
Additionally to the Navier-Stokes equations, at least with variable density, the transport equations for a reacting flow are the energy and species transport equations with their appropriate boundary conditions that may be of Dirichlet or Neumann type. In usual notations, the specie i transport equation is written as:
and the temperature transport equation:
The diffusion is modelled thanks to Fick's law that is a (usually good) approximation to the rigorous diffusion velocity calculation. Regarding the temperature transport equation, it is derived from the energy transport equation under the assumption of a low-Mach number flow (compressibility and viscous heating neglected). The low-Mach number approximation is suitable for the deflagration regime (as it will be demonstrated below), which is the main focus of combustion modelling. Hence, the transport equation for temperature, as a simplified version of the energy transport equation, is usually retained for the study of combustion and its modelling.
Note: The species and temperature equations are not closed as the fields of velocity and density also need to be computed. Through intense heat release in a very small area (the jump in temperature in typical hydrocarbon flames is about seven and so is the drop in density in this isobaric process, and the thickness of a flame is of the order of the millimetre), combustion influences the flow field. Nevertheless, the vast majority of combustion modelling has been developed based on the species and temperature equations, assuming simple flow fields, sometimes including hydrodynamics perturbations.
Low-Mach Number Equations
In compressible flows, when the motion of the fluid is not negligible compared to the speed of sound (which is the speed at which the molecules can reorganize themselves), the heap of molecules results in a local increase of pressure and temperature moving as an acoustic wave. It means that, in such a system, a proper reference velocity is the speed of sound and a proper pressure reference is the kinetic pressure. A contrario, in low-Mach number flows, the reference speed is the natural representative speed of the flow and the reference pressure is the thermodynamic pressure. Hence, the set of reference quantities to characterize a low-Mach number flow is given in the table below:
Density 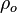 A reference density (upstream, average, etc.)
A reference density (upstream, average, etc.)
Velocity 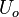 A reference velocity (inlet average, etc.)
A reference velocity (inlet average, etc.)
Temperature 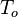 A reference temperature (upstream, average, etc.)
A reference temperature (upstream, average, etc.)
Pressure (static) 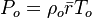 From Boyle-Mariotte
From Boyle-Mariotte
Length 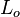 A reference length (representative of the domain)
A reference length (representative of the domain)
Time 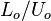
Energy 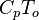 Internal energy at constant reference pressure.
Internal energy at constant reference pressure. 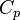 must also be chosen in a reference thermodynamical state.
must also be chosen in a reference thermodynamical state.
The equations for fluid mechanics properly adimensionalized can be written:
Mass conservation:
Momentum:
Total energy:
Specie:
State law:
The low-Mach number equations are obtained considering that 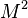 is small. 0.1 is usually taken as the limit, which recovers the value of a Mach number of 0.3 to characterize the incompressible regime.
is small. 0.1 is usually taken as the limit, which recovers the value of a Mach number of 0.3 to characterize the incompressible regime.
Considering the energy equation, in addition to the terms with 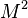 in factor in the equation, the total energy reduces to internal energy as:
in factor in the equation, the total energy reduces to internal energy as: 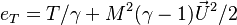 . Moreover, the work of pressure is considered as negligible because the gradient of pressure is negligible (low-Mach number approximation is indeed also named isobaric approximation) and the flow is assumed close to a divergence-free state.
For the same reason, volumic energy and enthalpy variations are assumed equal as they only differ through the addition of pressure. Hence, redimensionalized, the low-Mach number energy equation leads to the temperature equation as used in combustion analysis:
. Moreover, the work of pressure is considered as negligible because the gradient of pressure is negligible (low-Mach number approximation is indeed also named isobaric approximation) and the flow is assumed close to a divergence-free state.
For the same reason, volumic energy and enthalpy variations are assumed equal as they only differ through the addition of pressure. Hence, redimensionalized, the low-Mach number energy equation leads to the temperature equation as used in combustion analysis:
The Damköhler Number
A flame is a reaction zone. From this simple point of view, two aspects have to be considered: (i) the rate at which it is fed by reactants, let call 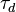 the characteristic time, and
the strength of the chemistry to consume them, let call the characteristic chemical time
the characteristic time, and
the strength of the chemistry to consume them, let call the characteristic chemical time 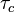 . In combustion, the Damköhler number, Da, compares these both time scales and, for that
reason, it is one of the most integral non-dimensional groups:
. In combustion, the Damköhler number, Da, compares these both time scales and, for that
reason, it is one of the most integral non-dimensional groups:
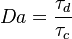 .
.
If Da is large, it means that the chemistry has always the time to fully consume the fresh mixture and turn it into equilibrium. Real flames are usually close to this state. The characteristic reaction time, 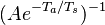 , is
estimated of the order of the tenth of a ms. When Da is low, the fresh mixture cannot be converted by a too weak chemistry. The flow remains frozen. This situation happens with ignition or misfire, for instance.
, is
estimated of the order of the tenth of a ms. When Da is low, the fresh mixture cannot be converted by a too weak chemistry. The flow remains frozen. This situation happens with ignition or misfire, for instance.
The picture of a deflagration lends itself to a description based on the Damköhler number. A reacting wave progresses towards the fresh mixture through preheating of the upstream closest layer. The elevation of the temperature strengthens the chemistry and reduces its characteristic time such that the mixture changes from a low-Da region (far upstream, frozen) to a high-Da region in the flame (intense reaction to equilibrium).
Conservation Laws
The processus of combustion transforms the chemical enthalpy into sensible enthalpy (i.e. rises the temperature of the gases thanks to the heat released). Simple relations can be drawn between species and temperature by studying the source terms appearing in the above equations:
Those coupling functions are named Schwalb-Zeldovich variables.
Hence 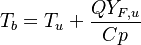 ,
, 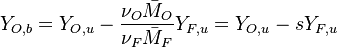 and
and 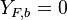 . Here, the example has been taken for a lean case.
. Here, the example has been taken for a lean case.
As mentioned in Sec. Main Specificities, the stoichiometric state is used to non-dimensionalize the conservation equations:
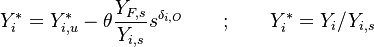 .
.
A comprehensive form of the reaction rate can be reconstituted to understand the difficulty of numerically resolving the reaction zone:
where 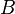 stands for all the constant terms present in this reaction rate, plus density.
stands for all the constant terms present in this reaction rate, plus density.
For the stoichiometric case and a global order of two, the reaction rate is graphed versus the reduced temperature for different values of the heat release and Zeldovitch parameter. A high value of  makes the reaction rate very sharp, versus temperature. It means that reaction is significant beyond a temperature level (sometimes called ignition temperature) that is close to one (the exponential term above is non-negligible for
makes the reaction rate very sharp, versus temperature. It means that reaction is significant beyond a temperature level (sometimes called ignition temperature) that is close to one (the exponential term above is non-negligible for 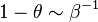 ). The heat release has qualitatively the same impact but not so strong. Transposed to the case of a flame sheet, it effectively shows that the reaction exists only in a fraction of the thermal thickness of the flame (the region close to the flame that the latter preheats, hence, where the reduced temperature rises from 0 to 1 here) where the temperature deviates few from the maximal one (density can be assumed as constant and equal to its burned-gas value). Numerically capturing such a sharp reaction zone can be costly and the lower values of
). The heat release has qualitatively the same impact but not so strong. Transposed to the case of a flame sheet, it effectively shows that the reaction exists only in a fraction of the thermal thickness of the flame (the region close to the flame that the latter preheats, hence, where the reduced temperature rises from 0 to 1 here) where the temperature deviates few from the maximal one (density can be assumed as constant and equal to its burned-gas value). Numerically capturing such a sharp reaction zone can be costly and the lower values of
 and
and 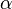 as presented here are usually preferred whenever possible.
as presented here are usually preferred whenever possible.
Most problems in combustion involve turbulent flows, gas and liquid
fuels, and pollution transport issues (products of combustion as well as for example noise
pollution). These problems require not only extensive experimental
work, but also numerical modelling. All combustion models must be validated
against the experiments as each one has its own drawbacks and limits. In this article, we will address the modeling fundamentals only.
The combustion models are often classified on their capability to deal with the different combustion regimes.
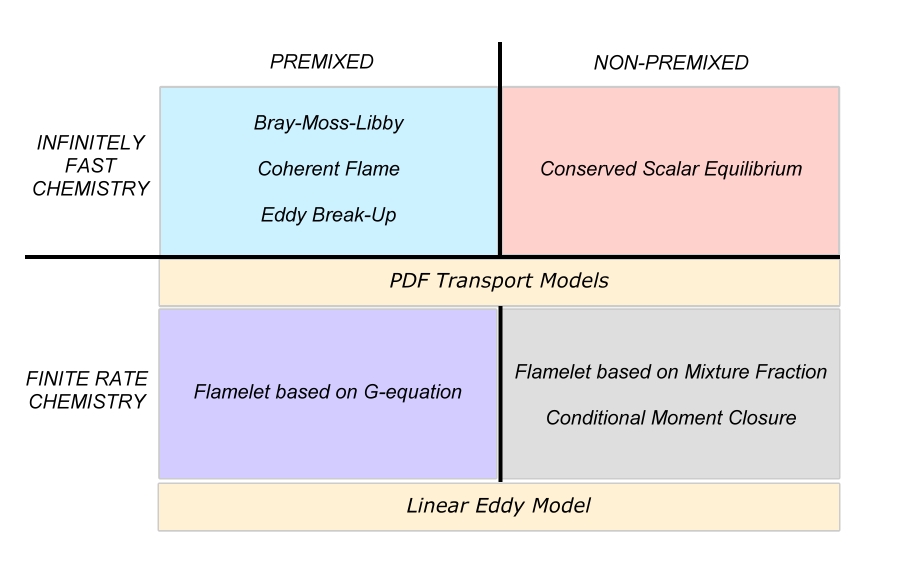
Three Combustion Regimes
Depending on how fuel and oxidizer are brought into contact in the combustion system, different combustion modes or regimes are identified. Traditionally, two regimes have been recognized: the premixed regime and the non-premixed regime. Over the last two decades, a third regime, sometime considered as a hybrid of the two former ones to a certain extend, has risen. It has been named partially-premixed regime.
The Non-Premixed Regime
This regime is certainly the easiest to understand. Everybody has already seen a lighter, candle or gas-powered stove. Basically, the fuel issues from a nozzle or a simple duct into the atmosphere. The combustion reaction is the oxidization of the fuel. Because fuel and oxidizer are in contact only in a limited region but are separated elsewhere (especially in the feeding system) this configuration is the safest. Diffusion of oxidant and fuel has to occur simultaneously to reaction to sustain combustion, the flame being a surface of separation of fuel and oxidant streams. The non-premixed flame has some other advantages. By controlling the flows of both reactants, it is (theoretically) possible to locate the stoichiometric interface, and thus, the location of the flame sheet. Moreover, the strength of the flame can also be controlled through the same process. Depending on the width of the transition region from the oxidizer to the fuel side, the species (fuel and oxidizer) feed the flame at different rates. This is because the diffusion of the species is directly dependent on the unbalance (gradient) of their distribution. A sharp transition from fuel to oxidizer creates intense diffusion of those species towards the flame, increasing its burning rate. This burning rate control through the diffusion process is certainly one of the reasons of the alternate name of such a flame and combustion mode: diffusion flame and diffusion regime.
Because a diffusion flame is fully determined by the inter-penetration of the fuel and oxidizer streams, it is convenient to introduce a tracer of the state of the mixture. This is the role of the mixture fraction, usually called Z or f. Z is usually taken as unity in the fuel stream and is null in the oxidizer stream. It varies linearly between this two bounds such that at any point of a frozen flow the fuel mass fraction is given by 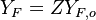 and the oxidizer mass fraction by
and the oxidizer mass fraction by 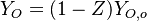 .
. 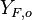 and
and 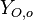 are the fuel and oxidizer mass fractions in the fuel and oxidizer streams, respectively.
The mixture fraction posses a transport equation that is expected to not have any source term as a tracer of a mixture must be a conserved scalar. First, the fuel and oxidizer mass fraction transport equations are written in usual notations:
are the fuel and oxidizer mass fractions in the fuel and oxidizer streams, respectively.
The mixture fraction posses a transport equation that is expected to not have any source term as a tracer of a mixture must be a conserved scalar. First, the fuel and oxidizer mass fraction transport equations are written in usual notations:
The two above equations are linearly combined in a single one in a manner that the source term disappears:
The quantity 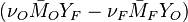 is thus a conserved scalar, one recognizes
one of the Schwalb-Zeldovich quantities introduced in Sec. Conservation Laws. One
also remarks that this transport equations combination is made in the equidiffusional approximation, i.e.
all the scalars, including temperature, diffuse at the same rate. The last step is to normalize it such that it equals unity in the pure fuel stream (
is thus a conserved scalar, one recognizes
one of the Schwalb-Zeldovich quantities introduced in Sec. Conservation Laws. One
also remarks that this transport equations combination is made in the equidiffusional approximation, i.e.
all the scalars, including temperature, diffuse at the same rate. The last step is to normalize it such that it equals unity in the pure fuel stream (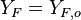 and
and 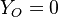 ) and is null in the pure oxidizer stream
(
) and is null in the pure oxidizer stream
(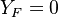 and
and 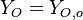 ). The resulting normalized passive scalar is the mixture fraction:
). The resulting normalized passive scalar is the mixture fraction:
governed by the transport equation:
The stoichiometric interface location (and thus the approximate location of the flame if the flow is reacting) is where 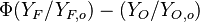 vanishes (or
vanishes (or 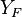 and
and 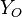 are both null in the reacting case). This leads to a stoichiometry definition:
are both null in the reacting case). This leads to a stoichiometry definition:
As the mixture fraction qualifies the degree of inter-penetration of fuel and oxidizer, the elements originally present in these molecules are conserved and can be directly traced back to the mixture fraction. This has led to an alternate defintion of the mixture fraction, based on element conservation.
First, the elemental mass fraction 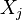 of element j is linked to the species mass fraction
of element j is linked to the species mass fraction 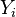 :
:
where 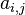 is a matrix counting the number of element j atoms in specie molecule named i and n is the number of species in the mixture.
The group pictured by the summation above is a linear combination of
is a matrix counting the number of element j atoms in specie molecule named i and n is the number of species in the mixture.
The group pictured by the summation above is a linear combination of 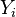 . Because the transport equations of species mass fraction, few lines earlier, are also linear, a transport equation for the elemental mass fraction can be written:
. Because the transport equations of species mass fraction, few lines earlier, are also linear, a transport equation for the elemental mass fraction can be written:
For mass is conserved, the linear combination of the source terms vanishes. Furthermore, by taking the same diffusion coefficient 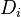 for all the species, the elemental mass fraction transport equation has exactly the same form as the specie transport equation (except the source term). Notice that the assumption of equal diffusion coefficient was also made in the previous definition of the mixture fraction and is justified in turbulent combustion modelling by the turbulence diffusivity flattening the diffusion process in high Reynolds number flows. Hence, the elemental mass fraction transport equation has the same structure as the mixture fraction transport equation seen above. Properly renormalized to reach unity in the fuel stream and zero in the oxidizer stream, the elemental mass fraction is a convenient way of determining the mixture fraction field in a flow. Indeed, it is widely used in practice for this purpose.
for all the species, the elemental mass fraction transport equation has exactly the same form as the specie transport equation (except the source term). Notice that the assumption of equal diffusion coefficient was also made in the previous definition of the mixture fraction and is justified in turbulent combustion modelling by the turbulence diffusivity flattening the diffusion process in high Reynolds number flows. Hence, the elemental mass fraction transport equation has the same structure as the mixture fraction transport equation seen above. Properly renormalized to reach unity in the fuel stream and zero in the oxidizer stream, the elemental mass fraction is a convenient way of determining the mixture fraction field in a flow. Indeed, it is widely used in practice for this purpose.
Simplified Diffusion Flame Solution
Because Schwalb-Zeldovitch variables rid off any source, they allow a first approximation of the flame description independent of the kinetics.
From the definition of 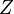 , the Schwalb-Zeldovich variables have the following expression:
, the Schwalb-Zeldovich variables have the following expression:
Two simplified limit cases for the diffusion flame equation can be built from those relations:
- In the frozen flow, the chemical source term is null everywhere. Hence,
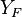 and
and 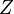 follow
follow
strictly the same linear transport equation. Then, 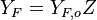 as anticipated above.
Follow:
as anticipated above.
Follow: 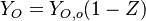 ,
, 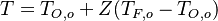 .
.
- The equilibrium solution, also with zero source term, the 'historical' diffusion flame description laid out by Burke and Schumann in 1928:
- Rich side:
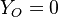 ,
, 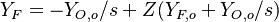 ,
, 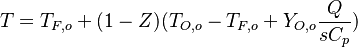
- Lean side:
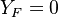 ,
, 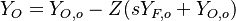 ,
, 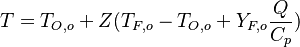
- Rich side:
From the value of 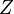 at stoichiometry above, the adiabatic flame temperature is obtained:
at stoichiometry above, the adiabatic flame temperature is obtained:
Remark 1: The Burke-Schumann solution for a diffusion flame, despite its age, is still one of the most used model, under some refreshments such as Mixed-Is-Burned, or Equilibrium combustion model where the burned value of the quantities is obtained by Gibbs function extrema instead of the full adiabatic consumption. The reason is that the concentration of the species and temperature can be calculated from the mixture fraction field, which is in turn described in terms of statistics in the turbulent flow.
Remark 2: In the Burke-Schuman solution, as the chemistry is infinitely fast, the flame is reduced to an interface separating the rich and lean sides. Therefore, quantities must be continuous at the flame and their gradients observe the jump conditions, from Sec. Conservation Laws:
Remark 3 From Remark 2, it is seen that the reactants fluxes must reach the flame in stoichiometric proportion (the fluxes and not the values themselves). Therefore, the relations developed in Remark 2 are true even without the equidiffusional approximation, whereas the relation based on 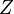 , no. On the other hand, the heat released by chemistry is conducted away from the flame thanks to the temperature gradients on both sides.
, no. On the other hand, the heat released by chemistry is conducted away from the flame thanks to the temperature gradients on both sides.
Dissipation Rate and Non-Equilibrium Effect
A very important quantity, derived from the mixture fraction concept, is the scalar dissipation rate, usually noted: 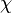 . In the above introduction to non-premixed combustion, it has been said that a diffusion flame is fully controlled through: (i) the position of the stoichiometric line, dictating where the flame sheet lies; (ii) the gradients of fuel on one side and oxidizer on the other side, dictating the feeding rate of the reaction zone through diffusion and thus the strength of combustion. According the the mixture fraction definition, the location of the stoichiometric line is naturally tracked through the
. In the above introduction to non-premixed combustion, it has been said that a diffusion flame is fully controlled through: (i) the position of the stoichiometric line, dictating where the flame sheet lies; (ii) the gradients of fuel on one side and oxidizer on the other side, dictating the feeding rate of the reaction zone through diffusion and thus the strength of combustion. According the the mixture fraction definition, the location of the stoichiometric line is naturally tracked through the 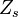 iso-line and it is seen here how the mixture fraction is a convenient tracer to locate the flame.
In the same manner, the mixture fraction field should also be able to give information on the strength of the chemistry as the gradients of reactants are directly linked to the mixture fraction distribution. The feeding rate of the reaction zone is characterized with the help of the inverse of a time. Because it is done through diffusion, it must be obtained through a combination of mixture fraction gradient and diffusion coefficient (dimensional analysis):
iso-line and it is seen here how the mixture fraction is a convenient tracer to locate the flame.
In the same manner, the mixture fraction field should also be able to give information on the strength of the chemistry as the gradients of reactants are directly linked to the mixture fraction distribution. The feeding rate of the reaction zone is characterized with the help of the inverse of a time. Because it is done through diffusion, it must be obtained through a combination of mixture fraction gradient and diffusion coefficient (dimensional analysis):
where the subscript s refers to quantities taken effectively where the reacting sheet is supposed to be, close to stoichiometry. This deduction of the scalar dissipation rate, scaling the feeding rate of the flame, is obtained here through physical arguments and is to be derived from equations below in a more mathematical manner. Note that the transport coefficient for the mixture fraction is identified to the one for temperature. This notation is usually used in the literature to emphasize that the rate of temperature diffusion (that is commensurable to the rate of species diffusion) is the retained parameter (as introduced in the following approach highlighting the role of the scalar dissipation rate). Depending if the diffusion process is free (mixing layer, boundary layer) or controlled (stagnation), the dissipation rate and then the non-premixed combustion may be of unsteady or steady nature.
Ignition / Burning / Extinction Curve
Let consider a mixing layer between fuel and oxidizer whose strain (and then intensity of reactant inter-diffusion) is carefully controlled. Let start from a flame already existing. Let also use the Damköhler number as defined above with the inverse of the scalar dissipation rate being the characteristic mechanical time of flow of reactants feeding the reaction zone. For high Da (low dissipation rate), the reactants diffuse slowly. The reaction is not very intense but the chemistry is fully achieved such that the maximum temperature is reached. Now, let decrease slowly (to avoid any unsteady effect on the chemistry) the Da. On one hand, the rate of feeding of flame through diffusion increases, and so does the reaction rate (that said, the reaction rate normalized by the dissipation rate decreases as the Da). On the other hand, the chemistry may not have the time to `eat' every reactant molecules that begin to leak through the flame: the fully sensible value is not realized and a lower temperature is achieved. With still increasing the dissipation rate, this mechanism leads to lower temperature in the flame zone down to a level that cannot be sustained by combustion (that strongly depends on temperature). The diffusion flame leaves the diffusion-controlled burning regime and extinguishes suddenly. It is said to be quenched. This is experienced in real life when blowing off a small wood fire. Slightly blowing increases the transfer between reactants and strengthens the reaction but blowing too much extinguishes the fire.
If now the start state is a frozen mixing layer between fuel and oxidant, at low Da (high dissipation rate), the flow remains frozen. When increasing Da, there will be a point where the chemistry will self-accelerate and the flame will light up through a sudden increase in temperature. Because the starting temperature is low, the ignition Da number is higher that the extinction Da above, exhibiting an hysteresis phenomenon.
When looking at the trend of the maximum temperature only versus Da, a curve with a shape in `S' appears, named as S-Curve for diffusion flames (see beside figure).
Flamelet Equation
In turbulent combustion modelling, the flamelet regime is identified as a regime that saves the integrity of the flame structure (Sec. The Wrinkled Regime). Turbulent eddies do not enter the structure and only contord the flame at a large scale. Therefore, it is usual to call the flamelet equation, the equation that describes the diffusion flame structure when not perturbed by turbulence. The model problem is usually retained as the counterflow diffusion flame. The strain imposed to the flame mimicks the one due to inhomogeneities in a real turbulent flow.
A counter-flow diffusion flame is basically made of two ducts, front-to-front, one issuing fuel at a mass fraction 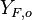 (may be diluted by an inert) and temperature
(may be diluted by an inert) and temperature 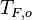 , and the other issuing oxidizer at a mass fraction
, and the other issuing oxidizer at a mass fraction 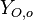 (the inert is usually di-nitrogen in air such that
(the inert is usually di-nitrogen in air such that 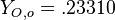 is a value commonly encountered) and temperature
is a value commonly encountered) and temperature 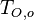 . A stretched mixging layer develops at the location the flows oppose. This stretch can be modulated by the flow rate from the feeding ducts. The diffusion flame sits around the iso-surface corresponding to stoichiometry. The figure beside sketches this widely used configuration, with the coordinate frame origin taken at the stagnation location in the middle of the mixing layer.
. A stretched mixging layer develops at the location the flows oppose. This stretch can be modulated by the flow rate from the feeding ducts. The diffusion flame sits around the iso-surface corresponding to stoichiometry. The figure beside sketches this widely used configuration, with the coordinate frame origin taken at the stagnation location in the middle of the mixing layer.
The Howarth-Dorodnitzyn transform and the Chapman approximation are applied to the above mixture fraction transport equation.
In the Chapman approximation, the thermal dependence of 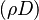 is approximated as
is approximated as 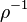 .
The Howarth-Dorodnitzyn transform introduces
.
The Howarth-Dorodnitzyn transform introduces 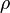 in the space coordinate system:
in the space coordinate system: 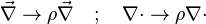 . The effect of these both mathematical operations is to `digest' the thermal variation of quantities such as density or transport coefficient. Hence, the mixture fraction equation comes in a simpler mathematical shape:
. The effect of these both mathematical operations is to `digest' the thermal variation of quantities such as density or transport coefficient. Hence, the mixture fraction equation comes in a simpler mathematical shape:
Here the references are taken in the stoichiometric zone (s subscript).
For the sake of simplicity, we shall use the potential flow result for this counter-flow problem with two identical jets although the presence of the flame (the associated density change) jeopardizes this theory, strictly speaking.
The velocity solution is thus:
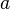 is named the stretch of the mixing layer and is the inverse of a time.
is named the stretch of the mixing layer and is the inverse of a time.
In such a flow, the transport equation for the mixture fraction may be written as a purely 1-D problem (assuming constant properties):
from which a `length' scale emerges for the mixing layer: 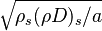 . Non-dimensionalized, with
. Non-dimensionalized, with 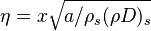 :
:
The boundary conditions may be approximated as 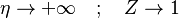 and
and
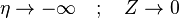 . Note that this approximation requires a thin layer compared to the counter-flow distance, and thus a relatively high strain rate.
Then, the solution for
. Note that this approximation requires a thin layer compared to the counter-flow distance, and thus a relatively high strain rate.
Then, the solution for 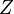 :
:
The scalar dissipation rate is deduced from this equation as:
Because combustion is highly temperature-dependent, T is certainly the scalar to which attention must be paid for. The temperature equation in the Low-Mach Number regime (Sec. Low-Mach Number Equations) is written below in steady-state:
After the Chapman approximation and the Howarth-Dorodnitzyn transform:
Here the references are taken in the flame, i.e. close to the stoichiometric line (s subscript).
In a non-premixed system, strictly speaking, 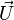 , is not really relevant as the flame is fully controlled by the diffusion process. Notwithstanding, in practice, non-premixed flames must be stabilized by creating a strain in the direction of diffusion. This is the reason why the velocity is left in the equation. Because a diffusion flame is fully described by the mixture fraction field, a change in coordinate can be applied:
, is not really relevant as the flame is fully controlled by the diffusion process. Notwithstanding, in practice, non-premixed flames must be stabilized by creating a strain in the direction of diffusion. This is the reason why the velocity is left in the equation. Because a diffusion flame is fully described by the mixture fraction field, a change in coordinate can be applied:
The Jacobian of the transform is given as:
Note that the diffusive layer of thickness 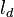 is defined as the region of transition between fuel and oxidizer and is thus given by the gradient of Z along the x direction.
This transform is applied to the vectorial operators:
is defined as the region of transition between fuel and oxidizer and is thus given by the gradient of Z along the x direction.
This transform is applied to the vectorial operators:
With this transform, the above temperature equation looks like:
As mentioned above, the velocity and the variation along the tangential direction to the main flame structure r are not supposed to play a major role. To be convinced, a variable scaling may be done, considering that the reaction zone extends
over a small fraction  of the diffusion thickness
of the diffusion thickness 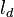 around stoichiometry. Then
the convective term of the above equation is
around stoichiometry. Then
the convective term of the above equation is 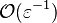 and the diffusive
term is
and the diffusive
term is 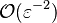 . By emphasizing the role of the gradient of Z along x as a key parameter defining the configuration the following equation is obtained:
. By emphasizing the role of the gradient of Z along x as a key parameter defining the configuration the following equation is obtained:
This equation (sometimes named the flamelet equation) serves as the basic framework to study the structure of diffusion flames. It highlights the role of the dissipation rate with respect to the strength of the source term and shows that the dissipation rate calibrates the combustion intensity.
Ignition
The flamelet equation may be used to explore the behaviour of the mixing-layer for not too high strain rate. As mentioned earlier, the Damköaut;hler may be high enough to allow a self-ignition. In this regime, the following assumptions may be made:
- the exponential argument in the reaction term,
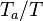 , is linearized around the frozen temperature value (indeed, as the activation temperature is large, a small change in the temperature from its frozen value is magnified in the reaction rate magnitude):
, is linearized around the frozen temperature value (indeed, as the activation temperature is large, a small change in the temperature from its frozen value is magnified in the reaction rate magnitude): 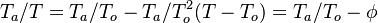 . It can be seen that a small change of temperature leading to
. It can be seen that a small change of temperature leading to 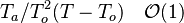 impacts the exponential term of the reaction rate.
impacts the exponential term of the reaction rate.
- the reactants may be approximated by their frozen flow values:
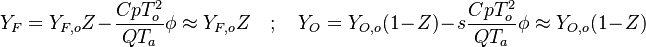 , under the hypothesis of large activation energy.
, under the hypothesis of large activation energy.
The flamelet equation is recast as:
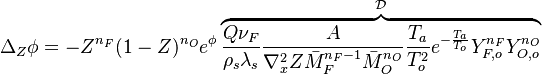 In this expression
In this expression 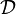 is a Damk\"ohler number.
is a Damk\"ohler number.
This expression must be solved numerically but, with the help of simplifications, an analytical solution may be found. It must be noticed that this analytical solution has no quantitative prediction capabilities. However, it is sufficient to illustrate the critical Damk\"ohler number for ignition for pedagogical purpose.
First, the equation is integrated from 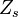 to
to 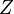 'somewhere in the rich side'.
'somewhere in the rich side'.
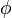 may be approximated as, on the asymptote
may be approximated as, on the asymptote 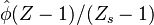 with a maximum
with a maximum  on the stoichiometric line, where ignition is supposed the strongest. Then, on the stoichiometric line, the derivative of
on the stoichiometric line, where ignition is supposed the strongest. Then, on the stoichiometric line, the derivative of 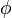 vanishes and, sufficiently far from the stoichiometric line it tends to
vanishes and, sufficiently far from the stoichiometric line it tends to 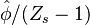 . To keep the solution simple, we choose the integration limit to be
on the border of the region where
. To keep the solution simple, we choose the integration limit to be
on the border of the region where 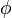 remains within 10% of its maximum such that it may be approximated as constant on the right hand side. The value of
remains within 10% of its maximum such that it may be approximated as constant on the right hand side. The value of 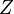 that fits this trade-off of being sufficiently far from
that fits this trade-off of being sufficiently far from 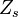 to allow the derivative of
to allow the derivative of 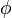 to reach its asymptote and
sufficiently close to prevent
to reach its asymptote and
sufficiently close to prevent 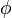 from decreasing is estimated to 40% of
from decreasing is estimated to 40% of 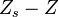 .
This estimation, quite disputable, is based on temperature profile observed in diffusion flames at low Da when the diffusive effect strongly smoothes it.
.
This estimation, quite disputable, is based on temperature profile observed in diffusion flames at low Da when the diffusive effect strongly smoothes it.
The end equation has the form:
This makes  a function of
a function of 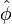 , maximum temperature in the ignition zone at
stoichiometry, that has a maximum for
, maximum temperature in the ignition zone at
stoichiometry, that has a maximum for 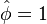 . This gives the bottom tipping point of the S-curve presented above. For the academical case
. This gives the bottom tipping point of the S-curve presented above. For the academical case 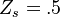 and
and 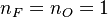 , this gives
, this gives 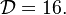 which is in a satisfactory agreement with the full numerical solution. It is interesting to note that the numerical solution follows the physics process of ignition of the diffusion layer by slowly increasing the Damk\"ohler number. Therefore, it cannot catch properly the turning point and the doubled-value relation. Instead, once the maximum Damk\"ohler number corresponding to ignition is reached, the reduced temperature soars sharply. Further increasing D in the forbidden range, no solution can be found. Physically, for larger values of the Damköhler number, the configuration jumps from this nearly frozen situation to an equilibrium situation with a well developed diffusion flame, see the S-Curve above. The simplified equation for ignition is thus unadapted and a specific solution for a developed diffusion flame is now to be presented.
which is in a satisfactory agreement with the full numerical solution. It is interesting to note that the numerical solution follows the physics process of ignition of the diffusion layer by slowly increasing the Damk\"ohler number. Therefore, it cannot catch properly the turning point and the doubled-value relation. Instead, once the maximum Damk\"ohler number corresponding to ignition is reached, the reduced temperature soars sharply. Further increasing D in the forbidden range, no solution can be found. Physically, for larger values of the Damköhler number, the configuration jumps from this nearly frozen situation to an equilibrium situation with a well developed diffusion flame, see the S-Curve above. The simplified equation for ignition is thus unadapted and a specific solution for a developed diffusion flame is now to be presented.
Diffusion Burning Process
From Sec. Simplified Solution of Diffusion Flame, the temperature jump at stoichiometry is identified as 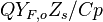 .
.
Although chemistry in a diffusion flame is usually very fast, one expects a very residual amount of reactants in the reaction zone laying along the stoichiometric line. It thus means that equilibrium is not reached in practice and that the temperature is somewhat lower than the equilibrium temperature. Thermodynamics is moderated by kinetics effects or, in other words, the curves T(Z) and Y(Z) depend on the dissipation rate and are not simply made of straight lines meeting at stoichiometry as in the simplified Burke-Schumann solution for diffusion flames.
To a certain extend, the flamelet equation Sec. Flamelet Equation may be used to present a solution for the non-premixed flame when the flame is already ignited, and the chemistry strength controlled by diffusion (we have stressed the author that an interesting aspect of diffusion flames is the ability to control the reaction rate through the level of mixing in the neighbourhood of the flame). As already emphasized, due to a strong non-linearity in temperature, the structure of a burning flame can never be far from the Burke-Schumann simplified solution.
Non-dimensionalized, the temperature solution in the flamelet may be written as:
in the rich side of the mixing layer, and:
in the lean side.
On recognizes the structure of the Burke-Schumann solution (Sec. Simplified Diffusion Flame Solution). 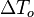 is the non-dimensionalized temperature difference between the reactants feed streams:
is the non-dimensionalized temperature difference between the reactants feed streams:
Those solutions are amended by the term 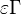 with
with 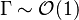 in the reaction zone and vanishing on the sides.
This amendment corresponds to the departure from the equilibrium solution due to kinetics effect. The quantity
in the reaction zone and vanishing on the sides.
This amendment corresponds to the departure from the equilibrium solution due to kinetics effect. The quantity  is taken small for the physical reasons explained above.
is taken small for the physical reasons explained above.
It is interesting to introduce 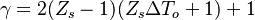 , combining the temperature difference between the reactant feeding streams and the stoichiometry of the combustion) as a synthetic parameter to inform about the geometry of the flame structure in the (Z,T) diagram (Burke-Schumann):
, combining the temperature difference between the reactant feeding streams and the stoichiometry of the combustion) as a synthetic parameter to inform about the geometry of the flame structure in the (Z,T) diagram (Burke-Schumann):
in the rich side of the mixing layer, and:
in the lean side.
For 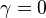 the slope in temperatue vs Z is the same on both sides of the flame. For
the slope in temperatue vs Z is the same on both sides of the flame. For 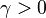 the rich side slope is the sharpest, and for
the rich side slope is the sharpest, and for 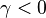 this is the lean side.
An interesting case is when
this is the lean side.
An interesting case is when 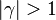 : one for the feeding stream enters the flame zone with a temperature higher than the flame temperature. In that case, whatever the dissipation rate, the flame is stretched with a hot stream
that sustains its temperature such that it is never extinguished.
: one for the feeding stream enters the flame zone with a temperature higher than the flame temperature. In that case, whatever the dissipation rate, the flame is stretched with a hot stream
that sustains its temperature such that it is never extinguished.
The departure in temperature from equilibrium in the reaction zone is reflected into the species concentrations, as it corresponds to still unburned reactants. With the help of the above Conservation Laws one finds:
- Lean side:
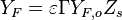 ,
, 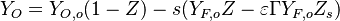
- Rich side:
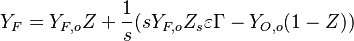 ,
, 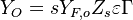
The picture beside illustrates the structure of a diffusion flame in its `normal' regime.
Recasting the Flamelet Equation above in terms of the reduced temperature, we find:
To describe the structure of the diffusion flame, the reduced mixture fraction is set:
The utility of the reduced mixture fraction is to focus on the reaction zone. This reaction zone is supposed located on the stoichiometric line (this is why the reduced mixture fraction is centred on 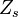 ) and to be very thin (reason of the introduction of the magnifying factor
) and to be very thin (reason of the introduction of the magnifying factor  ). One may convince oneself by considering in the above equation linking
). One may convince oneself by considering in the above equation linking 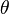 to
to 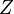 that one must stay close to the stoichiometric line if one wants
the non-equilibrium effect to be sensible compared to the adiabatic drop of the temperature. The equation is also written in terms of
that one must stay close to the stoichiometric line if one wants
the non-equilibrium effect to be sensible compared to the adiabatic drop of the temperature. The equation is also written in terms of 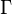 , the non-equilibrium departure rescaled by
, the non-equilibrium departure rescaled by  and the source term as
presented in Main Specificities of Combustion Chemistry is explicated:
and the source term as
presented in Main Specificities of Combustion Chemistry is explicated:
It is seen that one can form a Damköhler number as (see Sec. Damköhler Number for the general meaning of the Damköhler):
and that this number must scale with 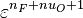 . So, to have a thin reaction zone, the Damköhler number must be high. Physically, it means that when fuel and oxidizer meet close to the stoichiometric line they combine quickly such that the reaction can be completed in a very narrow region.
. So, to have a thin reaction zone, the Damköhler number must be high. Physically, it means that when fuel and oxidizer meet close to the stoichiometric line they combine quickly such that the reaction can be completed in a very narrow region.
In the diffusion burning process, Da is sufficiently high to have 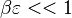 such that the departure from equilibirum for the temperature has no impact in the exponential term at the end of the RHS of the equations above. This exponential term approximates to unity (in the flame zone, so for small
such that the departure from equilibirum for the temperature has no impact in the exponential term at the end of the RHS of the equations above. This exponential term approximates to unity (in the flame zone, so for small 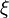 ). Physically, this is the Burke-Schumann solution when the chemistry is sufficiently fast such that the kinetics limitation (modelled by this exponential term in the reaction rate) is inexistent.
This gives more details on the structure of the diffusion flame for the simplified solution
presented above Sec. Simplified Diffusion Flame Solution. In particular, the relationship between Da and
). Physically, this is the Burke-Schumann solution when the chemistry is sufficiently fast such that the kinetics limitation (modelled by this exponential term in the reaction rate) is inexistent.
This gives more details on the structure of the diffusion flame for the simplified solution
presented above Sec. Simplified Diffusion Flame Solution. In particular, the relationship between Da and  allows an estimation of the quantities in the flame zone.
allows an estimation of the quantities in the flame zone.
As for the boundary conditions, in the diffusion regime, the chemistry is fast enough to deplete the reactants diffusing into the reaction zone. Then, no presence of fuel on the oxidizer side and vice versa is expected. In a concise manner, we must have:
Extinction
When, for a given Damköhler number, the Zeldovitch parameter is too high such that its product with  is no more negligible, the combustion regime enters an extinction process. Physically, the small departure from equilibrium is sufficient to impact the RHS exponential of the temperature equations above such that the non-linear temperature dependence is sensitive.
is no more negligible, the combustion regime enters an extinction process. Physically, the small departure from equilibrium is sufficient to impact the RHS exponential of the temperature equations above such that the non-linear temperature dependence is sensitive. 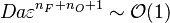 and
and 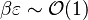 lead to the construction of a reduced
Damköhler number
lead to the construction of a reduced
Damköhler number 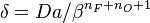 . This reduced Damköhler number is expected to be around unity in the extinction regime, meaning that the Da is still high enough to sustain combustion but that the non-linearity of combustion due to a high value of
. This reduced Damköhler number is expected to be around unity in the extinction regime, meaning that the Da is still high enough to sustain combustion but that the non-linearity of combustion due to a high value of  makes it very dependent to the temperature such that a weakening Damköhler, further enhancing the departure (temperature drop) from equilibrium, will quench the flame.
makes it very dependent to the temperature such that a weakening Damköhler, further enhancing the departure (temperature drop) from equilibrium, will quench the flame.
The fact that the chemistry is not fast enough to `eat' the reactants entering the flame and turn them into full equilibrium is synonymous to say that, at extinction, we expect a leakage of one or both reactants across the flame such that a concentration of the order of  may be found on the oxidizer side for the fuel and/or vice versa. This quantity is a function of
may be found on the oxidizer side for the fuel and/or vice versa. This quantity is a function of 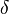 . When the leakage is too intense, the combustion is quenched. There is thus a quenching
. When the leakage is too intense, the combustion is quenched. There is thus a quenching 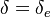 .
.
Depending on the value of 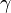 , as said above, the temperature slope on either side of the flame may be different. When reaching extinction, it is expected that the leakage happens for the reactant coming from the side with the weaker temperature slope through the side with the stronger temperature slope. The maximum temperature zone is lower than the adiabatic flame temperature, as previously mentioned, and also shifted towards the side of the flame with the weaker temperature slope. Hence, depending of the value of
, as said above, the temperature slope on either side of the flame may be different. When reaching extinction, it is expected that the leakage happens for the reactant coming from the side with the weaker temperature slope through the side with the stronger temperature slope. The maximum temperature zone is lower than the adiabatic flame temperature, as previously mentioned, and also shifted towards the side of the flame with the weaker temperature slope. Hence, depending of the value of 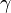 the flame at extinction is described by one of the two equations above. Fortunately, due to the symmetrical role of
the flame at extinction is described by one of the two equations above. Fortunately, due to the symmetrical role of 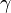 , a synthetic correlation for the Da at extinction can be obtained from the numerical solution of the above set of equations (with
, a synthetic correlation for the Da at extinction can be obtained from the numerical solution of the above set of equations (with 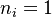 ):
):
This correlation, together with its equation now in a generic form for each side of the flame:
has an especial place in combustion theory and modelling. It has been first proposed in [3] in 1974 and is since used as a canonical equation for problems that may be reduced to. It is also at the heart of understanding of non-premixed combustion modelling such as the flamelet model that will be introduced later.
It is important to notice that due to the leakage of reactants at extinction, the boundary conditions must be weaker than for the diffusion controlled regime:
0 on the side where the flame lies at extinction (depending on 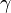 as seen above and where the equation is written) and 2 for the other.
as seen above and where the equation is written) and 2 for the other.
The idea is that, compared to the diffusion-controlled regime, the shape of the Burke-Schumann asymptotes is conserved but with a shift corresponding to the unburned leakage and the associated drop in sensible enthalpy. Then, compared to the diffusion-controlled regime the asymptotic boundary gradients are the same, but not the actual values.
In the case the flame is highly asymmetrical (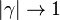 ) either because one of the reactant streams is preheated or because the stoichiometry is far from
) either because one of the reactant streams is preheated or because the stoichiometry is far from 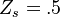 , an analytical approach may be found for
, an analytical approach may be found for 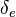 . This approach allows us to illustrate qualitatively the mechanism of extinction described only with words so far. Let take the case
. This approach allows us to illustrate qualitatively the mechanism of extinction described only with words so far. Let take the case 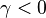 , meaning that the slopes (temperature and species) are sharper on the oxidizer side. Then, the maximum temperature zone is shifted on the fuel side (it may be seen for instance even for a moderate departure from the symmetry as in the figure above) and a leakage of fuel is expected on the oxidizer side.
In a first approximation, the leakage amount is approximated as
, meaning that the slopes (temperature and species) are sharper on the oxidizer side. Then, the maximum temperature zone is shifted on the fuel side (it may be seen for instance even for a moderate departure from the symmetry as in the figure above) and a leakage of fuel is expected on the oxidizer side.
In a first approximation, the leakage amount is approximated as 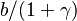 , with
, with 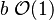 . So, for highly unsymmetrical flames (
. So, for highly unsymmetrical flames (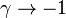 ), this leakage is considered important before extinction may occur. One may convince oneself by considering that the asymmetry is due to a preheating of the fuel stream. When
), this leakage is considered important before extinction may occur. One may convince oneself by considering that the asymmetry is due to a preheating of the fuel stream. When
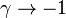 , it means that the preheating is such that the fuel stream temperature is close to the adiabatic temperature of the system. One may imagine that the flame is fairly robust and may bear a high level of leakage before being quenched. Actually, when
, it means that the preheating is such that the fuel stream temperature is close to the adiabatic temperature of the system. One may imagine that the flame is fairly robust and may bear a high level of leakage before being quenched. Actually, when 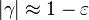 , by looking at the equation linking
, by looking at the equation linking 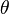 ,
,  , and
, and  , it is seen that an especial scaling happens between the non-equilibrium departure from the B-S solution and the drop of the B-S temperature away from stoichiometry. The non-premixed flame has thus the freedom to switch to a `premixed' regime on the side with the weakest temperature slope of the B-S solution and at a location corresponding to a strong chemistry. Hence, the fuel leakage on the oxidizer side is quantified as
, it is seen that an especial scaling happens between the non-equilibrium departure from the B-S solution and the drop of the B-S temperature away from stoichiometry. The non-premixed flame has thus the freedom to switch to a `premixed' regime on the side with the weakest temperature slope of the B-S solution and at a location corresponding to a strong chemistry. Hence, the fuel leakage on the oxidizer side is quantified as 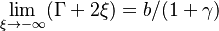 (remember the maximum temperature location is expected on the fuel side and the corresponding equation is used for the diffusion flame as developed above). The new asymptote intersects the
(remember the maximum temperature location is expected on the fuel side and the corresponding equation is used for the diffusion flame as developed above). The new asymptote intersects the 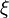 axis at the location
axis at the location
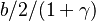 , that is taken as the flame position at extinction (in other words, the dissipation has the effect of shifting with respect to the Burke-Schumann infinitely fast chemistry / equilibrium).
, that is taken as the flame position at extinction (in other words, the dissipation has the effect of shifting with respect to the Burke-Schumann infinitely fast chemistry / equilibrium).
We use this shift to make a change of frame of reference, which is now centred around the flame position at extinction as just defined: 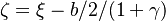 . The equation for the flame above becomes:
. The equation for the flame above becomes:
With this shift, stronger boundary conditions may be devised:
-
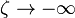 , we are on the oxidizer side of the flame in the new frame of reference and the fuel concentration must equals its leakage level, then
, we are on the oxidizer side of the flame in the new frame of reference and the fuel concentration must equals its leakage level, then 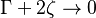 ,
,
-
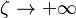 , given the fact that we are in the limit case
, given the fact that we are in the limit case 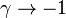 , it is expected that the oxidizer is consumed instead of leaking through the fuel side:
, it is expected that the oxidizer is consumed instead of leaking through the fuel side: 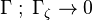 .
.
This equation may be simplified to the first order in 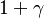 :
:
A first integral gives:
With the boundary conditions:
one obtains:
The RHS is a measure of the integrated reaction rate across the flame, which is a function of the leakage term b. One retrieves some of the arguments developed previously. This RHS is positive and increases in value with b up to a maximum corresponding to 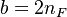 . Then it vanishes because the dissipation imposed to the flame is too strong for the chemistry. At this maximum, the minimum Damköhler that the flame can deal with is found, which is identified as the Damköhler number at extinction:
. Then it vanishes because the dissipation imposed to the flame is too strong for the chemistry. At this maximum, the minimum Damköhler that the flame can deal with is found, which is identified as the Damköhler number at extinction:
For 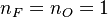 the first term of the correlation from [2] as provided above is recovered.
the first term of the correlation from [2] as provided above is recovered.
The figure beside illustrates the effect of the Damköhler number on the temperature profile across the flame (i.e. vs the
mixture fraction). Those solutions have been obtained from the flamelet equation presented above with reactant orders and free stream mass fractions equal to unity. The stoichiometry is 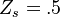 and the reactant free stream temperatures are the same. Two values of
and the reactant free stream temperatures are the same. Two values of 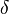 are chosen: 5, which is far from extinction and 2, which is relatively closer to extinction for this set of combustion parameters as seen below. It is retrieved that reducing the ratio chemistry strength / dissipation strength by reducing
are chosen: 5, which is far from extinction and 2, which is relatively closer to extinction for this set of combustion parameters as seen below. It is retrieved that reducing the ratio chemistry strength / dissipation strength by reducing 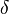 leads to a larger departure from equilibrium in the flame zone, around
leads to a larger departure from equilibrium in the flame zone, around 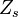 . The temperature profile is smoothed out in the flame.
. The temperature profile is smoothed out in the flame.
The figure on the right tracks the change in the maximal temperature in the flame zone for decreasing 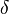 .
This figure illustrates well the non-linearity of combustion vs temperature: once the extinction value is passed, the temperature drop is as sharp as a cliff, meaning a sudden end of chemistry. Physically, this is what is experienced when blowing to much on a wood fire: as explained earlier, blowing reduces the Damköhler number. Below a threshold value, one experiences a sudden blow-off / extinction of the fire.
.
This figure illustrates well the non-linearity of combustion vs temperature: once the extinction value is passed, the temperature drop is as sharp as a cliff, meaning a sudden end of chemistry. Physically, this is what is experienced when blowing to much on a wood fire: as explained earlier, blowing reduces the Damköhler number. Below a threshold value, one experiences a sudden blow-off / extinction of the fire.
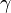 in the figure beside. It is retrieved that when the asymmetry is sensitive, there is considerable improvement of the flame robustness as predicted.
in the figure beside. It is retrieved that when the asymmetry is sensitive, there is considerable improvement of the flame robustness as predicted.
Remark: To develop this extinction analysis, we have assumed that the Zeldovitch parameter was asymptotically high. This is what is commonly named Asymptotic Energy Analysis (AEA). It uses the fact that combustion, under normal conditions, is highly temperature dependent by assuming that the activation temperature of the combustion chemistry tends to infinity. For the numerical simulation of the same extinction solutions, we use finite values of the Zeldovitch parameter. When the combustion parameters are scaled to values representative of actual chemistry, it is seen that the discrepancies with the AEA may be substantial. In order to get close to the analytical development, the numerical simulations must use unreasonably high values of the Zeldovitch parameter. It must also be noticed that pushing up to the second order the perturbation analysis will bring a correction that is even worse since it will predict an infinitely robust flame at 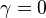 .
.
The Premixed Regime
In contrast to the non-premixed regime above, the reactants are here well mixed before entering the combustion chamber. Chemical reaction can occur everywhere and this flame can propagate upstream into the feeding system as a subsonic (deflagration regime) chemical wave. This presents lots of safety issues. Some situations prevent them: (i) the mixture is made too rich (lot of fuel compared to oxidizer) or too lean (too much oxidizer) such that the flame is close to its flammability limits (it cannot easily propagate); (ii) the feeding system and regions where the flame is not wanted are designed such that they impose strong heat loss to the flame in order to quench it. For a given thermodynamical state of the mixture (composition, temperature, pressure), the flame has its own dynamics (speed, heat release, etc) on which there is few control: the wave exchanges mass and energy through diffusion process in the fresh gases. On the other hand, those well defined quantities are convenient to describe the flame characteristics. The mechanism of spontaneous propagation
towards fresh gas through the thermal transfer from the combustion zone to the immediate slice of fresh gas
such that the ignition temperature is eventually reached for this latter was highlighted as early as by the end of the 19th century by Mallard and LeChatelier.
The reason the chemical wave is contained in a narrow region of reaction propagating upstream is the consequence of the discussion on the non-linearity of the combustion with temperature in the
Sec. Fundamental Aspects. It is of interest to compare the orders of magnitude of the temperature dependent term 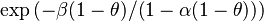 of the reaction source upstream in the fresh gas (
of the reaction source upstream in the fresh gas (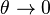 ) and in the reaction zone close to equilibrium temperature (
) and in the reaction zone close to equilibrium temperature (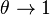 ) for the set of representative values:
) for the set of representative values: 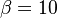 and
and
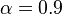 . It is found that the reaction is about
. It is found that the reaction is about 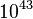 times slower in the fresh
gas than close to the burned gas. It is known that the chemical time scale is about 0.1 ms in the reaction zone of a typical flame, then the typical reaction time in the fresh gas in normal conditions is about
times slower in the fresh
gas than close to the burned gas. It is known that the chemical time scale is about 0.1 ms in the reaction zone of a typical flame, then the typical reaction time in the fresh gas in normal conditions is about
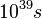 . To be compared with the order of magnitude of the estimated Universe age:
. To be compared with the order of magnitude of the estimated Universe age: 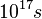 . Non-negligible chemistry is only confined in a thin reaction zone stuck to the hot burned gas at equilibrium temperature. In this zone, the #Damköhler number is high, in contrast to in the fresh mixture. It is natural and convenient to consider that the reaction rate is strictly zero everywhere except in this small reaction zone (one recovers the Dirac-like shape of the reaction profile,
provided that one can see the upstream flow as a region of increasing temperature towards the combustion zone and the downstream flow as in fully equilibrium).
. Non-negligible chemistry is only confined in a thin reaction zone stuck to the hot burned gas at equilibrium temperature. In this zone, the #Damköhler number is high, in contrast to in the fresh mixture. It is natural and convenient to consider that the reaction rate is strictly zero everywhere except in this small reaction zone (one recovers the Dirac-like shape of the reaction profile,
provided that one can see the upstream flow as a region of increasing temperature towards the combustion zone and the downstream flow as in fully equilibrium).
As the premixed flame is a reaction wave propagating from burned to fresh gases, the basic parameter is known to be the progress variable. In the fresh gas, the progress variable is conventionally put to zero. In the burned gas, it equals unity. Across the flame, the intermediate values describe the progress of the reaction to turn into burned gas the fresh gas penetrating the flame sheet. A progress variable can be set with the help of any quantity like temperature, reactant mass fraction, provided it is bounded by a single value in the burned gas and another one in the fresh gas. The progress variable is usually named c, in usual notations:
It is seen that c is a normalization of a scalar quantity. As mentioned above, the scalar transport equations are assumed linear such that the transport equation for c can be obtained directly. Actually, the transport equation for T (Sec. Transport Equations) is linear if constant heat capacity is further assumed (combustion of hydrocarbon in air implies a large excess of nitrogen whose heat capacity is only slightly varying) and the progress variable equation is directly obtained (here for a default of fuel - lean combustion):
The fact that the default or excess of fuel has been discussed above leads to the introduction of another quantity: the equivalence ratio. The equivalence ratio, usually noted 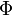 , is the ratio of two ratios. The first one is the ratio of the mass of fuel with the mass of oxidizer in the mixture. The second one is the same ratio for a mixture at stoichiometry. Hence, when the equivalence ratio equals unity, the mixture is at stoichiometry. If it is greater than unity, the mixture is named rich as there is an excess of fuel. In contrast, when it is smaller than unity the mixture is named lean. The equivalence ratio presented here for premixed flames has little connection with the equivalence ratio introduced earlier regarding the non-premixed regime. Basically, the equivalence ratio as defined for non-premixed flames gives the equivalence ratio of a premixed mixture with the same mass of fuel and oxidizer. Moreover, the equivalence ratio as defined for a premixed mixture can be obtained based on the mixture fraction (it is thus the local equivalence ratio at a point in the non-homogeneous mixture described by the mixture fraction). From the definitions given above:
, is the ratio of two ratios. The first one is the ratio of the mass of fuel with the mass of oxidizer in the mixture. The second one is the same ratio for a mixture at stoichiometry. Hence, when the equivalence ratio equals unity, the mixture is at stoichiometry. If it is greater than unity, the mixture is named rich as there is an excess of fuel. In contrast, when it is smaller than unity the mixture is named lean. The equivalence ratio presented here for premixed flames has little connection with the equivalence ratio introduced earlier regarding the non-premixed regime. Basically, the equivalence ratio as defined for non-premixed flames gives the equivalence ratio of a premixed mixture with the same mass of fuel and oxidizer. Moreover, the equivalence ratio as defined for a premixed mixture can be obtained based on the mixture fraction (it is thus the local equivalence ratio at a point in the non-homogeneous mixture described by the mixture fraction). From the definitions given above:
Premixed Flame Péclet Number
Earlier in this section, it has been said that a premixed flame posses its own dynamics, as a free propagating surface, and has thus characteristic quantities. For this reason, a Péclet number may be defined, based on these quantities. The Péclet number has the same structure as the Reynolds number but the dynamical viscosity is replaced by the ratio of the thermal conductivity and the heat capacity of the mixture. The thickness 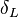 of a premixed flame is essentially thermal. It means that it corresponds to the distance of the temperature rise between fresh and burned gases. This thickness is below the millimetre for conventional flames. The width of the reaction zone inside this flame is even smaller, by about one order of magnitude. This reaction zone is stuck to the hot side of the flame due to the high thermal dependency of the combustion reactions, as seen above. Hence, the flame region is essentially governed by a convection-diffusion process, the source term being negligible in most of it.
of a premixed flame is essentially thermal. It means that it corresponds to the distance of the temperature rise between fresh and burned gases. This thickness is below the millimetre for conventional flames. The width of the reaction zone inside this flame is even smaller, by about one order of magnitude. This reaction zone is stuck to the hot side of the flame due to the high thermal dependency of the combustion reactions, as seen above. Hence, the flame region is essentially governed by a convection-diffusion process, the source term being negligible in most of it.
It is convenient to write the progress variable transport equation in a steady-state framework. The quantities at flame temperature (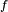 ) are used to non-dimensionalize the equation:
) are used to non-dimensionalize the equation:
Note that the source term is neglected, consistently with what has been said above. This convection-diffusion equation makes appear a first approximation of a flame Péclet number:
From the Péclet number, it is possible to obtain an expression for the flame velocity (remembering that 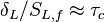 , vid. inf. Sec. Three Turbulent-Flame Interaction Regimes):
, vid. inf. Sec. Three Turbulent-Flame Interaction Regimes):
For typical hydrocarbon flames, the speed is some tens of centimetres per second and the diffusivity is some
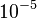 square metres per second. The chemical time in the reaction zone of about one tenth of a millisecond is recovered.
square metres per second. The chemical time in the reaction zone of about one tenth of a millisecond is recovered.
Details of the Premixed Unstrained Planar Flame
A plane combustion wave propagating in a homogeneous fresh mixture is the reference case to describe the premixed regime. At constant speed, it is convenient to see the flame at rest with a flowing upstream mixture. This is actually the way propagating flames are usually stabilized. In the frame of description, the
physics is 1-D, steady with a uniform (the flame is said unstrained) mass flowing across the system. Two types of equations are thus sufficient to describe the problem, the temperature transport equation and the species transport equations, as in Sec. Transport Equations. The transport coefficients will be chosen as equal: 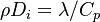 (unity Lewis numbers). Suppose the 1-D domain is described thanks to a conventional (Ox) axis with a flame propagating towards negative x (this is the conventional usage), the boundary conditions are:
(unity Lewis numbers). Suppose the 1-D domain is described thanks to a conventional (Ox) axis with a flame propagating towards negative x (this is the conventional usage), the boundary conditions are:
- in the frozen mixture:
-
- in the burned gas region supposed at equilibrium:
-
- in the frozen mixture:
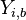 and
and 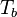 are obtained from Sec. Conservation Laws.
are obtained from Sec. Conservation Laws.
The quantities that have been mentioned just above (scalar and temperature profiles, mass flow rate through the system) are the solution to be sought.
According to the discussions above, the temperature transport equation in its full normalized form may be written as (lean /stoichiometric case):
This equation is further simplified by the variable change 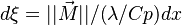 :
:
Although somewhat out of scope, the existence and unicity of the solution of this type of equation are usually demonstrated with the help of the Schauder Theorem and Maximum Principle. From the point of view of physicists and engineers, the solution that is found analytically is de facto considered as the unique solution of the equation.
Scenarii of Combustion Process in the Phase Portrait
In the frame moving with the flame, both phase variables are the reduced temperature and its gradient. To ease the reading with usual notations, it is written: 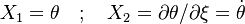 . The system arises:
. The system arises:
with 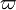 being the full source term in the above equation.
being the full source term in the above equation.
In the frame moving with the flame, two singular nodes are found in the frozen flow  and the equilibrium region
and the equilibrium region 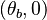 , i.e when
, i.e when 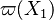 vanishes.
vanishes.
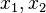 are defined as small departures from the singular nodes such that the linearized system in their neighbourhood is:
are defined as small departures from the singular nodes such that the linearized system in their neighbourhood is:
provided: 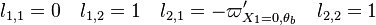 .
The characteristic polynom is, in usual notations:
.
The characteristic polynom is, in usual notations: 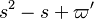 such that the eigenvalues are:
such that the eigenvalues are:
A priori, those eigenvalues may be (i) real distinct, (ii) real identical, or (iii) conjugated complex. In the first case, the orbits in the phase diagram are organized, in the immediate neighbourhood of the singular node, with respect to the eigenvectors directions associated to the eigenvalues. The following task is to identify the nature of those eigenvalues and of the corresponding nodes. Because 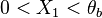 is bounded, complex eigenvalues are excluded as they would lead to a spiral node. This remark is important for the node on the cold side as it imposes a bound:
is bounded, complex eigenvalues are excluded as they would lead to a spiral node. This remark is important for the node on the cold side as it imposes a bound:
As the mass flow rate through the flame is included into 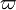 , it imposes a minimum value on the flame speed to tackle with the cold boundary difficulty (rise of the chemical rate in the frozen flow). In this condition, it
is an unstable node (improper in case of equality).
On the other hand, because
, it imposes a minimum value on the flame speed to tackle with the cold boundary difficulty (rise of the chemical rate in the frozen flow). In this condition, it
is an unstable node (improper in case of equality).
On the other hand, because 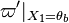 is not positive, the node on the hot side is found as a saddle point. The overall scenario of combustion within the flame is thus an orbit leaving the cold node to join the hot node by branching on a trajectory compatible with the negative eigenvalue of the saddle.
is not positive, the node on the hot side is found as a saddle point. The overall scenario of combustion within the flame is thus an orbit leaving the cold node to join the hot node by branching on a trajectory compatible with the negative eigenvalue of the saddle.
It must be noted that the associated eigenvectors are of the form:
that is, on the cold node, a positive departure on 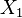 following any of the two eigendirections, leads
to a consistent creation of positive temperature gradient, while on the hot node, only the stable direction will allow a consistent creation of a positive temperature gradient for any departure of the temperature towards region where it is inferior to
following any of the two eigendirections, leads
to a consistent creation of positive temperature gradient, while on the hot node, only the stable direction will allow a consistent creation of a positive temperature gradient for any departure of the temperature towards region where it is inferior to 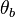 . Another remark is the structure of the eigendirections. The leaving directions on the cold node have a slope larger than the one of
. Another remark is the structure of the eigendirections. The leaving directions on the cold node have a slope larger than the one of 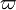 while the stable direction of the hot node has a slope smaller than the one of
while the stable direction of the hot node has a slope smaller than the one of 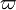 . It means that there is some point where the orbit must cross the profile of the chemical term versus temperature. For that temperature, the gradient equals the reaction rate through construction of the phase space. When looking back to the equation of the premixed flame, it happens in a region of inflexion for the temperature (the second order derivative must vanish). Furthermore, at this intersection, the orbit is horizontal (if the frame of reference for
. It means that there is some point where the orbit must cross the profile of the chemical term versus temperature. For that temperature, the gradient equals the reaction rate through construction of the phase space. When looking back to the equation of the premixed flame, it happens in a region of inflexion for the temperature (the second order derivative must vanish). Furthermore, at this intersection, the orbit is horizontal (if the frame of reference for 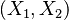 is Cartesian) due to the shape of the premixed flame equation above that can be recast into
is Cartesian) due to the shape of the premixed flame equation above that can be recast into 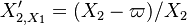 .
Close to the cold node, the orbits have a shape of parabola whose axis is the direction with the largest eigenvalue magnitude.
Close to the hot node, the orbits have an hyperboloid shape with asymptots as the eigendirections. Now the ingredients are here to draw a sketchy scenario of the combustion in a premixed flame. It will be superimposed on the reaction rate graph studied in Sec. Fundamentals.
Some typical orbits from the above analysis are drawn in the figure on the right. The basic geometrical arguments developed are reproduced. In particular, the dashed lines represent forbidden orbits by the physics (boundedness of
.
Close to the cold node, the orbits have a shape of parabola whose axis is the direction with the largest eigenvalue magnitude.
Close to the hot node, the orbits have an hyperboloid shape with asymptots as the eigendirections. Now the ingredients are here to draw a sketchy scenario of the combustion in a premixed flame. It will be superimposed on the reaction rate graph studied in Sec. Fundamentals.
Some typical orbits from the above analysis are drawn in the figure on the right. The basic geometrical arguments developed are reproduced. In particular, the dashed lines represent forbidden orbits by the physics (boundedness of 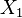 , irreversibility). Orbits must be travelled from left to right, corresponding to increasing free parameter
, irreversibility). Orbits must be travelled from left to right, corresponding to increasing free parameter  .
It is of integral importance to remember that, in combustion in conventional conditions, the source term is highly non-linear. Therefore, it is localized in a very thin sheet and, upstream,
.
It is of integral importance to remember that, in combustion in conventional conditions, the source term is highly non-linear. Therefore, it is localized in a very thin sheet and, upstream,  and
and 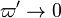 .
Only the most unstable eigendirection of the cold node is compatible as an orbit. The other trajectories, being paraboloidal, are tangent to the other direction that is flat at the limit. It physically means an elevation of temperature in bulk, that is contradictory to what is expected from a highly non-linear combustion term. Hence, the additional orbit in red is the one expected in idealized combustion conventional conditions.
.
Only the most unstable eigendirection of the cold node is compatible as an orbit. The other trajectories, being paraboloidal, are tangent to the other direction that is flat at the limit. It physically means an elevation of temperature in bulk, that is contradictory to what is expected from a highly non-linear combustion term. Hence, the additional orbit in red is the one expected in idealized combustion conventional conditions.
The following picture is the result of actual computations of the above 1-D flame equation (stoichiometry and 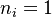 ) with the help of a high-order (6) code. The already presented combinations of
) with the help of a high-order (6) code. The already presented combinations of  and
and
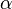 are used and the orbits are retrieved. For most of the cases, as predicted above, the system selects a solution leaving the cold node with the most unstable direction (identifiable with its slope close to unity for vanishing
are used and the orbits are retrieved. For most of the cases, as predicted above, the system selects a solution leaving the cold node with the most unstable direction (identifiable with its slope close to unity for vanishing
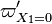 ). There is also an additional curve, for
). There is also an additional curve, for 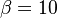 with the denominator of the exponential argument suppressed. This curve is remarkable as the solution selected by the system leaves the cold node in a manner fully controlled by the
with the denominator of the exponential argument suppressed. This curve is remarkable as the solution selected by the system leaves the cold node in a manner fully controlled by the 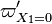 . This is a very singular solution, not expected in combustion in conventional conditions, as explained above. The purpose of this remark is to question the well-posedness of considering simplifying the exponential argument for
. This is a very singular solution, not expected in combustion in conventional conditions, as explained above. The purpose of this remark is to question the well-posedness of considering simplifying the exponential argument for  "sufficiently high", as it is usually proposed for this type of modelling. As observed, the dynamical system analysis demonstrates a switch in the nature of the solution selected.
At the physical level, when the orbit follows the most unstable direction with a slope close to unity, it means that
"sufficiently high", as it is usually proposed for this type of modelling. As observed, the dynamical system analysis demonstrates a switch in the nature of the solution selected.
At the physical level, when the orbit follows the most unstable direction with a slope close to unity, it means that 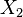 "follows"
"follows" 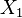 , which is a signature of a diffusion process. In other words, the preheating mechanism of a premixed flame propagation as proposed for more than one century is in work. On the other hand, when
, which is a signature of a diffusion process. In other words, the preheating mechanism of a premixed flame propagation as proposed for more than one century is in work. On the other hand, when
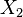 is dependent on the evolution of
is dependent on the evolution of 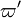 , it shows that "cold" chemistry drives the solution in the frozen flow and not the acknowledged mechanism of deflagration.
, it shows that "cold" chemistry drives the solution in the frozen flow and not the acknowledged mechanism of deflagration.
Flame Solution
As already mentioned, the flame system may be split into three zones. Upstream, the conventional mechanism of deflagration
is supported by diffusion of heat. Downstream, the mixture is at equilibrium after combustion. In between, there exists the reaction layer. For large  the reaction layer is very thin such that it can be seen as a discontinuity between the fresh and burned gases. This is this difference in scales that introduces the use of the asymptotic method to resolve some of the flame characteristics, such as speed, time, heat region thickness, or reaction zone thickness.
the reaction layer is very thin such that it can be seen as a discontinuity between the fresh and burned gases. This is this difference in scales that introduces the use of the asymptotic method to resolve some of the flame characteristics, such as speed, time, heat region thickness, or reaction zone thickness.
The domain is partitioned, according to this zoning defined by the scales driving the physics with an outer domain, driven by large scales and an inner domain refining the description within the discontinuity. If the discontinuity (flame reaction zone) is at 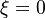 , everywhere but 0, the equation is simplified as:
, everywhere but 0, the equation is simplified as:
- For
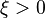 , it is expected that the mixture has reached equilibrium chemistry, such that:
, it is expected that the mixture has reached equilibrium chemistry, such that: 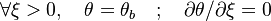 .
.
- For
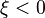 , this is the preheat zone and the solution is
, this is the preheat zone and the solution is 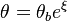 with
with 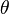 reaching
reaching 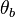 at the disconstinuity and vanishing, together with its gradient, far upstream in the frozen mixture.
at the disconstinuity and vanishing, together with its gradient, far upstream in the frozen mixture.
The solution for the species and the value of 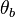 are obtained from Conservation Equations above. The 'big picture' is thus an exponential variation in the thermal thickness matched with a plateau in the downstream region, the line of matching being the discontinuity (flame) that has no thickness at this scale of description.
are obtained from Conservation Equations above. The 'big picture' is thus an exponential variation in the thermal thickness matched with a plateau in the downstream region, the line of matching being the discontinuity (flame) that has no thickness at this scale of description.
To refine the analysis in the discontinuity region, a magnifying factor  is used to stretch the coordinates:
is used to stretch the coordinates: 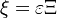 . The inner solution is thus a slowly-varying function of
. The inner solution is thus a slowly-varying function of 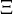 . Hence, in this inner region, the equation for the premixed flame becomes:
. Hence, in this inner region, the equation for the premixed flame becomes:
In order to stretch and 'look inside' a discontinuity,  is very small. It yields two remarks:
is very small. It yields two remarks:
- convection is negligible compared to diffusion. The heat losses from the reaction zone are essentially diffusion driven.
- The reaction zone is governed by a diffusion-reaction budget and the reaction term
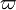 must be strong to balance the intense heat loss due to the sharp diffusion (the zone is very thin, hence the gradients are sharp).
must be strong to balance the intense heat loss due to the sharp diffusion (the zone is very thin, hence the gradients are sharp).
The mechanism is thus different from the outer region that was convection-diffusion driven.
Each quantity is developed in a series of  .
At the leading order, for
.
At the leading order, for 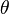 , in the lean case, the conservation relations (Sec. Conservation Laws) yield:
, in the lean case, the conservation relations (Sec. Conservation Laws) yield:
where 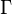 is the first-order development of the departure of
is the first-order development of the departure of 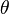 from the maximum value due to the incomplete combustion, and
from the maximum value due to the incomplete combustion, and 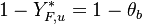 is the reduction of temperature for non-stoichiometric cases. Injected into the above equation:
is the reduction of temperature for non-stoichiometric cases. Injected into the above equation:
Although the full develoment is not achieved, a number of scaling may be highlighted:
- because the temperature cannot be much below unity,
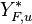 must be close to 1
must be close to 1  . For clarity, it is not expanded in an
. For clarity, it is not expanded in an  series.
series.
- The denominator of the exponential argument simplifies to unity for small
 .
.
- To get a finite rate in the reaction zone,
 scales with
scales with 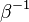 .
.
The burning rate eigenvalue, 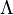 , is naturally expanded as:
, is naturally expanded as: 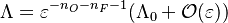 . The low-order equation to be solved is:
. The low-order equation to be solved is:
The boundary conditions are obtained from the matching of the outer solutions on the right and left sides of the flame as written above (the outer solutions are reached at infinity for a very small magnifying factor  ).
Once integrated with respect to those boundary conditions, the burning-rate eigenvalue (from which
).
Once integrated with respect to those boundary conditions, the burning-rate eigenvalue (from which  is extracted) is obtained as:
is extracted) is obtained as:
The RHS integral is not developed for clarity but presents no peculiar difficulties.
The development has been carried out at the first order in  . As soon as a second order development is attempted, some expressions are no more analytically tractable. On the other hand, a second order development allows introduce the temperature-dependent trends of some terms in
. As soon as a second order development is attempted, some expressions are no more analytically tractable. On the other hand, a second order development allows introduce the temperature-dependent trends of some terms in  . Physical results are retrieved such as a slight decrease of the speed for a positive sensitivity of transport parameters to temperature around equilibrium conditions.
. Physical results are retrieved such as a slight decrease of the speed for a positive sensitivity of transport parameters to temperature around equilibrium conditions.
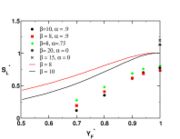
 and
and 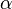 are used. Very high values of
are used. Very high values of  (and thus negligible effect of
(and thus negligible effect of 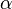 are also presented to show the problem of slow convergence for finite value of the Zeldovitch parameter. Not that
are also presented to show the problem of slow convergence for finite value of the Zeldovitch parameter. Not that 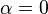 does not mean an athermal reaction but the mathematical simplification of the denominator of the exponential argument of the source term.
does not mean an athermal reaction but the mathematical simplification of the denominator of the exponential argument of the source term.The image beside illustrates the response of the premixed flame speed with respect to fuel concentration (chosen as the limiting component here; equivalent findings are obtained for default of oxidizer) for different values of the chemical parameters  and
and 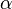 (as noted above, the pre-exponential constant
(as noted above, the pre-exponential constant 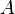 impacts only the overall magnitude). The theoretical expression (continuous line) is tested against a 1-D high accuracy
code with the given chemistry implemented. It is seen that:
impacts only the overall magnitude). The theoretical expression (continuous line) is tested against a 1-D high accuracy
code with the given chemistry implemented. It is seen that:
- the Zeldovitch parameter drives the drop for non-stoichiomeric mixtures,
- the drop is relatively well modelled by the theoretical expression, and
- the absolute magnitude converges slowly towards the theoretical one when increasing
 in the code (effect of the finiteness of
in the code (effect of the finiteness of  in the real case).
in the real case).
The picture exhibiting profiles for different Zeldovitch and heat release parameters shows the factual impact: upstream, the exact exponential profile is recovered and corresponds to the pre-heating region (thermal thickness). In the reaction zone (just upstream of the extremum), the departure from the exact solution is due to the kinetic effect. This kinetic effect is more pronounced when  is lower because the lower the Zeldovitch parameter, the lower the temperature reaction zone can be without leading to extinction. The flame takes this opportunity to maximize its transfer in heat and reactant with the cold zone. This is the physical understanding of an inverse dependence of the maximum flame speed with
is lower because the lower the Zeldovitch parameter, the lower the temperature reaction zone can be without leading to extinction. The flame takes this opportunity to maximize its transfer in heat and reactant with the cold zone. This is the physical understanding of an inverse dependence of the maximum flame speed with  .
.
Modification of the Flame Speed with Curvature
When the thickness of the flame 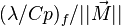 is considered small compared to inhomogeneities existing in the flow, the flame can be reduced to an interface between fresh and burned gases. This interface may not be strictly plan in the general case. For instance, when the interface is curved towards the burned gas, it offers a larger opportunity for transfer of mass and heat with the fresh gas. As the ability of the chemistry to burn the coming matter is limited, the flame has thus to reduce its displacement speed. The figure beside provides a 2-D sketch of this situation that happens in contorded turbulent fields. Curvature effect is thus an ingredient appearing in combustion models.
is considered small compared to inhomogeneities existing in the flow, the flame can be reduced to an interface between fresh and burned gases. This interface may not be strictly plan in the general case. For instance, when the interface is curved towards the burned gas, it offers a larger opportunity for transfer of mass and heat with the fresh gas. As the ability of the chemistry to burn the coming matter is limited, the flame has thus to reduce its displacement speed. The figure beside provides a 2-D sketch of this situation that happens in contorded turbulent fields. Curvature effect is thus an ingredient appearing in combustion models.
To mathematically give the expression showing that the curvature influences the flame speed (for small curvature), the non-dimensionalized temperature equation across a planar premixed flame above is slightly recast:
In this expression, 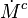 is the flame mass flow rate when perturbed by a curvature normalized by the reference one developed above.
is the flame mass flow rate when perturbed by a curvature normalized by the reference one developed above. 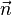 is the normal to the iso-temperature pointing towards the fresh gas, what is named the normal to the flame. From the expression developed above and for a slightly perturbed flame, the gradients, production and diffusion terms are very close to the unperturbed flame. Only the last term, the normal divergence, does not exist for a non-perturbed flame. Hence, the above equation may be simplified against the one for unperturbed flame presented earlier:
is the normal to the iso-temperature pointing towards the fresh gas, what is named the normal to the flame. From the expression developed above and for a slightly perturbed flame, the gradients, production and diffusion terms are very close to the unperturbed flame. Only the last term, the normal divergence, does not exist for a non-perturbed flame. Hence, the above equation may be simplified against the one for unperturbed flame presented earlier:
This is the divergence of the flame normal that contains the information upon geometrical perturbation (curvature) that impacts the speed.
The key is thus to get an idea of the geometrical significance of the normal divergence. The normal divergence theorem says that this is the sum of the principal curvatures of the flame surface at the location considered. To give a good mental picture, the simplest configuration without loss of generality is to consider the flame surface approached by an osculatory revolution ellipsoid, as in the figure beside. The location of the approximation is the intersection of the Ox axis and the flame surface in red (where the ellipsoid is tangent to the flame). At this location, the normal divergence is the sum of the curvature of the basic ellipse (before its rotation around Oy) at its minor extremum, and the curvature of the circle corresponding to the rotation of this point around Oy when the 3-D shape is formed. Giving a lecture on conical coordinate systems is beyond the purpose but the interested reader may want to follow the corresponding steps to check this result: (i) write the divergence of a vector in the ellipsoid coordinate system, (ii) consider that the vector is the normal, i.e. it has only one constant component perpendicular to the local ellipsoidal iso-coordinate, to simplify the divergence expression, (iii) split the resulting terms into two parts by identifying the second derivative of the basic shape 2-D ellipse as one principal curvature, and the inverse of the radius of the circle corresponding to the rotation of the ellipse around Oy at the point where the flame surface is approached, in the figure this is simply the minor axis of the ellipse.
The expression is readily written as:
where 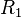 and
and 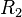 are the two radius of curvature (non-dimensionalized by the reference flame thickness) local to the surface.
For instance, they are the small axis of the basic ellipse and its radius of curvature at its minor maximum when the
surface is approached by the osculatory ellipsoid as above.
are the two radius of curvature (non-dimensionalized by the reference flame thickness) local to the surface.
For instance, they are the small axis of the basic ellipse and its radius of curvature at its minor maximum when the
surface is approached by the osculatory ellipsoid as above.
Natural Instabilities of Premixed Flames
Another aspect accounted for in turbulent combustion modelling of premixed flame is the creation of flame surface (corrugation) by hydrodynamics instabilities. These instabilities have been mentioned by Darrieus as early as 1938. The motivation of discussing about this is also related to the framework of description used that is widely employed for combustion models development. This framework is named the hydrodynamics limit, where the flame is isolated as a zero-thickness interface in the flow, and has been first introduced just above. In this framework, any diffusive and energetic aspects disappear and the set of equations is limited to two incompressible Euler systems. One system in the fresh gases (with a constant density of cold mixture). One system in the burned gases (with a constant density of mixture at equilibrium).
To understand the basic properties of a premixed flame leading to the birth of instabilities, it is first important to realize that a premixed flame, in the hydrodynamic limit, behaves as a dioptre with a refractive index in the burned gases larger than in the fresh gases. For a flow with an angle of attack on the flame (i.e. a flame not strictly 1-D perpendicular to the flow), the tangential component of the flow speed relative to the flame surface is conserved while the normal component is accelerated by a factor corresponding to the ratio of the density in order to conserve mass flow across the interface. Hence, the streamlines are pushed towards the normal to the flame when crossing, that is similar to rays of light entering a refracting medium.
If one considers a region of a premixed flame that bumps a little bit towards the fresh gas (see figure beside -- the same approach is symmetrically true for the bump towards the burned gas), the local stream tube slightly opens on the bumpy interface before being refracted and coming back to its original section at constant mass flow rate. Hence, just in front of the bump, the gas velocity in this stream tube decreases and does not oppose the flame motion, allowing the bump to increase in magnitude. This is the fundamental mechanism of such instabilities.
The equations sets are in usual notations:
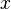 is the coordinate used above along the flame path and
is the coordinate used above along the flame path and 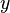 is in the tangential plan.
is in the tangential plan.
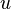 and
and 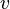 are the respective velocities.
Those equations may be normalized by steady-state reference quantities such as flame speed, flame length, gauge pressure and density with respect to fresh gas properties and are written on both sides of the interface.
are the respective velocities.
Those equations may be normalized by steady-state reference quantities such as flame speed, flame length, gauge pressure and density with respect to fresh gas properties and are written on both sides of the interface.
These sets of equations must match at the interface (flame surface) through conservation of mass flow rate and momentum:
The subscripts 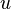 and
and 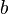 stand for unburned and burned sides, respectively. The subscript
stand for unburned and burned sides, respectively. The subscript 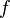 points the interface. In these equations, the flame motion
points the interface. In these equations, the flame motion 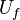 is reintroduced because we want to track the instability movement over the mean position of the flame. This instability motion is described by the equation
is reintroduced because we want to track the instability movement over the mean position of the flame. This instability motion is described by the equation 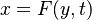 such that the motion of the interface normal to itself is obtained as:
such that the motion of the interface normal to itself is obtained as:
with a normal to the front:
As the instability motion is considered at its birth, i.e. when it is still small, the quantities are linearized with  as a small parameter:
as a small parameter:
The Eulerian system is reduced to (at the first order in  , the order zero is simplified for homogeneous flow):
, the order zero is simplified for homogeneous flow):
The one-sided equations for the jump conditions become (terms up to the first order in  are kept):
are kept):
The following jump conditions are obtained (by recalling that unburned steady-state quantities are chosen as references):
- From the first equation at the order 0,
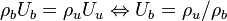
- From the first equation at the order 1,
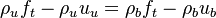
- From the second equation at the order 0,
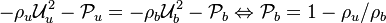
- From the second equation at the order 1,
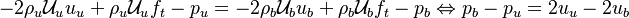
- From the third equation at order 1 (no order 0),
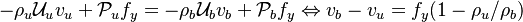
The solution for the linearized, autonomous Euler system is:
where one recognizes an account for the perturbation of the field in the  direction (
direction ( ), the wave number of the instability following
), the wave number of the instability following  ,
,  and the
growth rate with time
and the
growth rate with time 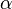 .
The eigenvalues of the system are used to determine the
.
The eigenvalues of the system are used to determine the 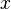 dependence of the solution
dependence of the solution 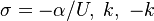 , with the positive ones applying on the fresh side and the negative ones on the burned size to have a vanishing perturbation far from the flame.
, with the positive ones applying on the fresh side and the negative ones on the burned size to have a vanishing perturbation far from the flame.
The eigenmodes give the flow pertubations on either side of the flame:
The jump conditions above applied to this perturbation field yield the following system (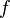 has also been put into the harmonic form
has also been put into the harmonic form 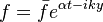 ):
):
Additionaly, from the definition of the flame path 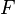 , we have the kinematic relation
, we have the kinematic relation
 .
.
The above set of equations forms a system of four unknowns  for a given (but unknown) shape information on the flame bump
for a given (but unknown) shape information on the flame bump 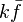 .
Solving for the growth rate gives:
.
Solving for the growth rate gives:
This third-degree polynom has three solutions, namely the dispersion relation found by Darrieus, a stable mode, and the trivial solution (with no physical meaning), respectively:
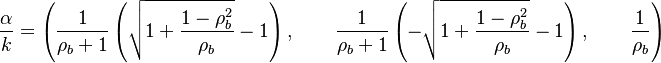
Remark 1 By considering the shape of the eigenvectors giving the perturbation, one recovers that, upstream of the flame, the flow is potential (the rotational of the velocity vector is null and we have chosen a constant density flow, that is barotropic and divergence free), while downstream, additionally to another
perturbation of the potential type, one finds a vorticity mode (the mode with the eigenvalue  . The drift of vorticity at the crossing of the flame front is a known property of flames.
. The drift of vorticity at the crossing of the flame front is a known property of flames.
Remark 2 In more conventional literature, the strange trivial solution for the instability growth rate is swept under the rug. Given the pedagogical nature of this electronic documentation, we can dig a little bit as the appearance of this trivial, fool solution is a good example of some modelling issue. It is important to realize that a mathematical model and the physics it describes belong to different realities. Hence, the mathematical model will generate all the solutions that the mathematics can reach in its own space. Some of them are still connected to the physics. Some others, like this trivial solution, belongs only to the mathematical solution space, an indirect way of pointing out a model limitation. The model under scope here is the hydrodynamic limit. In this model, the domain is divided into two subdomains, one upstream of the flame interface, one downstream, that are put in relation with each other through a limited number of jump conditions. In reality, the physics connects these both domains much more tightly. The curious reader will have observed that the trivial solution makes the equation system for  (i.e. for a fixed growth rate) undetermined, and so are the jump conditions. By generating this trivial solution, the mathematics decouples both domains. The information coming from upstream to downstream (thanks to the shape of the linearized Euler system), a solution is found only for the upstream domain, the downstream being not solved and remains undetermined in lack of information. This solution cannot happen in reality because the fresh and burned gases in a real system are connected by many aspects, and not only by the jump conditions.
(i.e. for a fixed growth rate) undetermined, and so are the jump conditions. By generating this trivial solution, the mathematics decouples both domains. The information coming from upstream to downstream (thanks to the shape of the linearized Euler system), a solution is found only for the upstream domain, the downstream being not solved and remains undetermined in lack of information. This solution cannot happen in reality because the fresh and burned gases in a real system are connected by many aspects, and not only by the jump conditions.
Stretch / Compression of Premixed Flame
The last of the `big' three turbulent ingredients (including aforementioned curvature and instabilities) impacting the flame at the local level is the compression or stretch of a premixed flame due to inhomogeneities in the flow, likely to happen with turbulence.
The physics is pictured in the beside figure. In the flame area, the mass flow rate along the main direction may decrease (or increase) with distance. In a frame of reference whose origin is the core of the flame, a stretch (compression) results due to the difference in mass flow rate entering and leaving the flame zone. Important Remark Here, we are interested in the inhomogeneity in the mass flow rate along one direction only. We do NOT write that the flame volume is a region of mass source/sink.
In the same manner as above for the curvature effect, we introduce a (small) inhomogeneity of the flow as
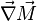 such that the following equation can be substracted from the unperturbed flame equation.
such that the following equation can be substracted from the unperturbed flame equation.
Hence, for a small perturbation, the linearized dependence of the flame on stretch/compression is:
The Partially-Premixed Regime
This regime is somewhat less academics and has been recognized two decades ago. It is acknowledged as a hybrid of the premixed and the non-premixed regimes but the degree of interaction of these two modes of combustion to accurately describe a partially-premixed flame is still not well understood. It can be simply pictured by a lifted diffusion flame. Let us consider fuel issuing from a nozzle into the air. If the exit velocity is large enough, for some fuels, the flame lifts off the rim of the nozzle. It means that below the flame base, fuel and oxidizer have room to premix. Hence, the flame base propagates into a premixed mixture. However, it cannot be reduced to a premixed flame (although it is often simplified as this): (i) the mixing is not perfect and the different parts of the flame front constituting the flame base burn in mixtures of different thermodynamical states. This provides those parts with different deflagration capabilities such that the flame base has a complex shape. Indeed, it is convex, naturally leaded by the part burning at stoichiometry, unless `exotic' feeding temperatures are used. (ii) Because the mixture is not homogeneous, transfer of species and temperature driven by diffusion occurs in a direction perpendicular to the propagation of the flame base. Because the flame front is not flat, those transfers act as a connection vehicle across the different parts of the leading front. (iii) The unburned left downstream by the sections of the leading front not burning at stoichiometry diffuse towards each other to form a diffusion flame as described above. The connection of the leading front with the trailing diffusion flame has been evidenced as complicated and the siege of transfers of species and temperature. These two last items are the state-of-the-art difficulties in understanding those flames and do not appear in the models although it has been demonstrated they have a major impact and are certainly a fundamental characteristic of partially-premixed flames.
The partially-premixed flame is usually described using c and Z as introduced earlier. Because the framework is essentially non-premixed, the mixture fraction is primarily used to describe the flame. Regarding the head of the flame where partial-premixing has an impact, each part of the front is described with a local progress variable. The need of defining a local progress variable is that each section of the partially-premixed front has a different equivalence ratio leading to a different definition of c:
Three Turbulent-Flame Interaction Regimes
It may appear odd to try to describe here what is the reason of combustion modelling research: the interaction of the turbulence with chemistry. However, one of the first steps in building knowledge in turbulent combustion was the qualitative exploration of what might be the dynamics of a flame in a turbulent environment. This led to what is now known as combustion diagrams. As explained above, the premixed regime lends itself the easiest to such an approach as it exhibits natural intrinsic quantities which are not as objectively identifiable in the other combustion regimes. Note that these quantities may depend on the geometry of the flame: for instance turbulence can bend a flame sheet, leading to a change in its dynamics compared to the flat flame propagating in a medium at rest. In this section, the turbulence-flame interaction modes will be described for a premixed flame. Only remarks will be added regarding the non-premixed and partially-premixed regimes.
An integral quantity to assess the interaction between a premixed flame sheet and the turbulence is the Karlovitz number Ka. It compares the characteristic time of flame displacement with the characteristic time of the smallest structures (that are also the fastest) of the turbulence.
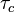 is the chemical time of the flame. To estimate it, it is necessary to come back to the above progress variable transport equation in a steady-state framework.
is the chemical time of the flame. To estimate it, it is necessary to come back to the above progress variable transport equation in a steady-state framework.
The premixed wave propagates at a speed 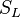 because it is fed by reactants diffusing inside the combustion zone and which are preheated because temperature diffuses in the reverse direction. The speed at which the flame progresses is thus related to the rate of species diffusion into the reaction zone which are then consumed. As the premixed flame is a free propagating wave whose speed of propagation is only limited by the chemical strength, the characteristic chemical time is based only on the diffusion and the mass flow rate experienced by the flame:
because it is fed by reactants diffusing inside the combustion zone and which are preheated because temperature diffuses in the reverse direction. The speed at which the flame progresses is thus related to the rate of species diffusion into the reaction zone which are then consumed. As the premixed flame is a free propagating wave whose speed of propagation is only limited by the chemical strength, the characteristic chemical time is based only on the diffusion and the mass flow rate experienced by the flame:
The smallest eddies are the ones being dissipated by the viscous forces. Their characteristic time is estimated thanks to a combination of the viscosity and the flux of turbulent energy to be dissipated (also called turbulent dissipation 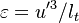 ):
):
Thanks to those definitions of chemical and small structure times, it is possible to give another definition of the Karlovitz number:
which is the square of the ratio between the premixed flame thickness and the small structure scale: Ka actually compares scales. To arrive to this latter result, the three following assumptions must be used: (i) the flame thickness is obtained thanks to the premixed flame Péclet number (vid. sup.); (ii) the turbulence small structure (Kolmogorov eddies) scale is given by: 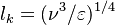 following the same dimensional argument as for the estimation of its time; and (iii) scalar diffusion scales with viscosity.
following the same dimensional argument as for the estimation of its time; and (iii) scalar diffusion scales with viscosity.
Remark Regarding the Diffusion Flame
From what has been presented above, a diffusion flame does not have characteristic scales. Setting a turbulence combustion regime classification for non-premixed flames has still not been answered by research. Some laws of behaviour will only be drawn around the scalar dissipation rate which is the parameter of integral importance for a diffusion flame.
Indeed, the dynamics of a diffusion flame is determined by the strain rate imposed by the turbulence. As for the premixed flames, the shortest eddies (Kolmogorov) are the ones having the largest impact. The diffusive layer is thus given by the size of the Kolmogrov eddies: 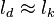 and the typical diffusion time scale (feeding rate of the reaction zone) is given by the characteristic time of the Kolmogorov eddies:
and the typical diffusion time scale (feeding rate of the reaction zone) is given by the characteristic time of the Kolmogorov eddies: 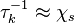 as the Reynolds number of the Kolmogorov structures is unity. Here,
as the Reynolds number of the Kolmogorov structures is unity. Here, 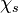 is the sample-averaging of
is the sample-averaging of 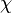 based on (conditioned) stoichiometric conditions, where the flame is expected to be.
based on (conditioned) stoichiometric conditions, where the flame is expected to be.
The Wrinkled Regime
This regime is also called the flamelet regime. Basically, it assumes that the flame structure is not affected by turbulence. The flame sheet is convoluted and wrinkled by eddies but none of them is small enough to enter it. Locally magnifying, the laminar flame structure is maintained.
This regime exists for a Karlovitz number below unity (vid. sup.), i.e. chemical time smaller than the small structure time or flame thickness smaller than small structure scale. Notwithstanding, the laminar flame dynamics can be disrupted for 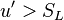 . In that case, although the flame structure is not altered by the small structures, it can be convected by large structures such that areas of different locations in the front interact. It shows that, even with a small Karlovitz number, the turbulence effect is not always weak.
. In that case, although the flame structure is not altered by the small structures, it can be convected by large structures such that areas of different locations in the front interact. It shows that, even with a small Karlovitz number, the turbulence effect is not always weak.
The Corrugated Regime
The formal definition of a flame is the region of temperature rise. However, the volume where the reaction takes place is about one order of magnitude smaller, embedded inside the temperature rise region and close to its high temperature end. Hence, there exist some levels of turbulence creating eddies able to enter the flame zone but still large enough to not affect the internal reaction sheet. In other words, the flame thermal region is thickened by turbulence but the reaction zone is still in the wrinkled regime. This situation is called the Corrugated Regime.
Due to the structure of the Karlovitz number, once written in terms of length scales (vid. sup.), this situation arises for an
increase of the Karlovitz number by two orders of magnitude compared to the value for the wrinkled regime. Hence, in the range
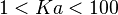 , the laminar structure of the reaction zone is still preserved but not the one of the preheat zone.
, the laminar structure of the reaction zone is still preserved but not the one of the preheat zone.
The Thickened Regime
In this last case, turbulence is intense enough to generate eddies able to affect the structure of the reaction zone as well. In practice, it is expected that those eddies are in the tail of the energy spectrum such that their lifetime is very short. Their impact on the reaction zone is thus limited.
Obviously, Ka > 100. A topological description is of little relevance here and a well-stirred reactor model fits better.
Reaction mechanisms
Combustion is mainly a chemical process. Although we can, to some extent, describe a flame without any chemistry information, modelling of the flame propagation requires the knowledge of speeds of reactions, product concentrations, temperature, and other parameters. Therefore fundamental information about reaction kinetics is essential for any combustion model. A fuel-oxidizer mixture will generally combust if the reaction is fast enough to prevail until all of the mixture is burned into products. If the reaction is too slow, the flame will extinguish. If too fast, explosion or even detonation will occur. The reaction rate of a typical combustion reaction is influenced mainly by the concentration of the reactants, temperature, and pressure.
A stoichiometric equation for an arbitrary reaction can be written as:
|
|
where  denotes the stoichiometric coefficient, and
denotes the stoichiometric coefficient, and 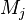 stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction.
stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction.
The reaction rate, expressing the rate of disappearance of reactant i, is defined as:
|
|
in which k is the specific reaction rate constant. Arrhenius found that this constant is a function of temperature only and is defined as:
|
|
where A is pre-exponential factor, E is the activation energy, and  is a temperature exponent. The constants vary from one reaction to another and can be found in the literature.
is a temperature exponent. The constants vary from one reaction to another and can be found in the literature.
Reaction mechanisms can be deduced from experiments (for every resolved reaction), they can also be constructed numerically by the automatic generation method (see [Griffiths (1994)] for a review on reaction mechanisms). For simple hydrocarbons, tens to hundreds of reactions are involved. By analysis and systematic reduction of reaction mechanisms, global reactions (from one to five step reactions) can be found (see [Westbrook (1984)]).
Governing equations for chemically reacting flows
Together with the usual Navier-Stokes equations for compresible flow (See Governing equations), additional equations are needed in reacting flows.
The transport equation for the mass fraction 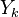 of k-th species is
of k-th species is
where Ficks' law is assumed for scalar diffusion with 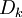 denoting the species difussion coefficient, and
denoting the species difussion coefficient, and 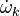 denoting the species reaction rate.
denoting the species reaction rate.
A non-reactive (passive) scalar (like the mixture fraction 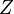 ) is goverened by the following transport equation
) is goverened by the following transport equation
where 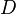 is the diffusion coefficient of the passive scalar.
is the diffusion coefficient of the passive scalar.
RANS equations
In turbulent flows, Favre averaging is often used to reduce the scales (see Reynolds averaging) and the mass fraction transport equation is transformed to
where the turbulent fluxes 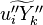 and reaction terms
and reaction terms
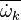 need to be closed.
need to be closed.
The passive scalar turbulent transport equation is
where 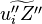 needs modelling. A common practice is to model the turbulent fluxes using the
gradient diffusion hypothesis. For example, in the equation above the flux
needs modelling. A common practice is to model the turbulent fluxes using the
gradient diffusion hypothesis. For example, in the equation above the flux 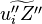 is modelled as
is modelled as
where 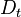 is the turbulent diffusivity. Since
is the turbulent diffusivity. Since 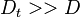 , the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.
, the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.
In addition to the mean passive scalar equation,
an equation for the Favre variance 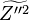 is often employed
is often employed
where 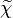 is the mean Scalar dissipation rate
defined as
is the mean Scalar dissipation rate
defined as 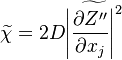 This term and the variance diffusion fluxes needs to be modelled.
This term and the variance diffusion fluxes needs to be modelled.
LES equations
The Large eddy simulation (LES) approach for reactive flows introduces equations for the filtered species mass fractions within the compressible flow field. Similar to the #RANS equations, but using Favre filtering instead of Favre averaging, the filtered mass fraction transport equation is
where 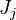 is the transport of subgrid fluctuations of mass fraction
is the transport of subgrid fluctuations of mass fraction
and has to be modelled.
Fluctuations of diffusion coefficients are often ignored and their contributions are assumed to be much smaller than the apparent turbulent diffusion due to transport of subgrid fluctuations. The first term on the right hand side is then
Infinitely fast chemistry
All combustion models can be divided into two main groups according to the assumptions on the reaction kinetics. We can either assume the reactions to be infinitely fast - compared to e.g. mixing of the species, or comparable to the time scale of the mixing process. The simple approach is to assume infinitely fast chemistry. Historically, mixing of the species is the older approach, and it is still in wide use today. It is therefore simpler to solve for #Finite rate chemistry models, at the overshoot of introducing errors to the solution.
Premixed combustion
Premixed flames occur when the fuel and oxidiser are homogeneously mixed prior to ignition. These flames are not limited only to gas fuels, but also to the pre-vaporised fuels. Typical examples of premixed laminar flames is bunsen burner, where the air enters the fuel stream and the mixture burns in the wake of the riser tube walls forming nice stable flame. Another example of a premixed system is the solid rocket motor where oxidizer and fuel and properly mixed in a gum-like matrix that is uniformly distributed on the periphery of the chamber. Premixed flames have many advantages in terms of control of temperature and products and pollution concentration. However, they introduce some dangers like the autoignition (in the supply system).
Turbulent flame speed model
Eddy Break-Up model
The Eddy Break-Up model is the typical example of mixed-is-burnt combustion model. It is based on the work of Magnussen, Hjertager, and Spalding and can be found in all commercial CFD packages. The model assumes that the reactions are completed at the moment of mixing, so that the reaction rate is completely controlled by turbulent mixing. Combustion is then described by a single step global chemical reaction
|
|
in which F stands for fuel, O for oxidiser, and P for products of the reaction. Alternativelly we can have a multistep scheme, where each reaction has its own mean reaction rate. The mean reaction rate is given by
|
|
where  denotes the mean concentrations of fuel, oxidiser, and products
respectively. A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for all the situations. Care must be taken especially in highly strained regions, where the ratio of
denotes the mean concentrations of fuel, oxidiser, and products
respectively. A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for all the situations. Care must be taken especially in highly strained regions, where the ratio of  to
to  is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually have some remedies to overcome this problem.
is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually have some remedies to overcome this problem.
This model largely over-predicts temperatures and concentrations of species like CO and other species. However, the Eddy Break-Up model enjoys a popularity for its simplicity, steady convergence, and implementation.
Bray-Moss-Libby model
Non-premixed combustion
Non premixed combustion is a special class of combustion where fuel and oxidizer
enter separately into the combustion chamber. The diffusion and mixing of the two streams
must bring the reactants together for the reaction to occur.
Mixing becomes the key characteristic for diffusion flames.
Diffusion burners are easier and safer to operate than premixed burners.
However their efficiency is reduced compared to premixed burners.
One of the major theoretical tools in non-premixed combustion
is the passive scalar mixture fraction  which is the
backbone on most of the numerical methods in non-premixed combustion.
which is the
backbone on most of the numerical methods in non-premixed combustion.
Conserved scalar equilibrium models
The reactive problem is split into two parts. First, the problem of mixing , which consists of the location of the flame surface which is a non-reactive problem concerning the propagation of a passive scalar; And second, the flame structure problem, which deals with the distribution of the reactive species inside the flamelet.
To obtain the distribution inside the flame front we assume it is locally one-dimensional and depends only on time and the scalar coodinate.
We first make use of the following chain rules
and transformation
upon substitution into the species transport equation (see #Governing Equations for Reacting Flows), we obtain
The second and third terms in the LHS cancel out due to continuity and mixture fraction transport. At the outset, the equation boils down to
where 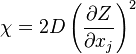 is called the scalar dissipation
which controls the mixing, providing the interaction between the flow and the chemistry.
is called the scalar dissipation
which controls the mixing, providing the interaction between the flow and the chemistry.
If the flame dependence on time is dropped, even though the field  still depends on it.
still depends on it.
If the reaction is assumed to be infinetly fast, the resultant flame distribution is in equilibrium.
and 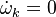 . When the flame is in equilibrium, the flame configuration
. When the flame is in equilibrium, the flame configuration 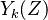 is independent of strain.
is independent of strain.
Burke-Schumann flame structure
The Burke-Schuman solution is valid for irreversible infinitely fast chemistry. With a reaction in the form of
|
|
If the flame is in equilibrium and therefore the reaction term is 0.
Two possible solution exists, one with pure mixing (no reaction)
and a linear dependence of the species mass fraction with 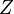 .
Fuel mass fraction
.
Fuel mass fraction
Oxidizer mass fraction
Where 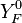 and
and 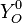 are fuel and oxidizer mass fractions
in the pure fuel and oxidizer streams respectively.
are fuel and oxidizer mass fractions
in the pure fuel and oxidizer streams respectively.
The other solution is given by a discontinuous slope at stoichiometric mixture fraction
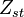 and two linear profiles (in the rich and lean side) at either
side of the stoichiometric mixture fraction.
Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.
and two linear profiles (in the rich and lean side) at either
side of the stoichiometric mixture fraction.
Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.
and oxidizer mass fraction
Finite rate chemistry
Premixed combustion
Coherent flame model
Flamelets based on G-equation
Flame surface density model
Non-premixed combustion
Flamelets based on conserved scalar
Peters (2000) define Flamelets as "thin diffusion layers embedded in a turbulent non-reactive flow field".
If the chemistry is fast enough, the chemistry is active within a thin region
where the chemistry conditions are in (or close to) stoichiometric conditions, the "flame" surface.
This thin region is assumed to be smaller than Kolmogorov length scale and therefore the
region is locally laminar. The flame surface is defined as an iso-surface of a certain scalar 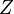 ,
mixture fraction in #Non premixed combustion.
,
mixture fraction in #Non premixed combustion.
The same equation used in #Conserved scalar models for equilibrium chemistry is used here but with chemical source term different from 0
This approach is called the Stationary Laminar Flamelet Model (SLFM) and has the advantage that
flamelet profiles 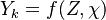 can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.
For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory COSILAB [1] with its relevant solver RUN1DL, which can be used for a variety of relevant geometries; see various publications that are available for download. Other software tools are available such as CHEMKIN [2] and
CANTERA [3].
can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.
For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory COSILAB [1] with its relevant solver RUN1DL, which can be used for a variety of relevant geometries; see various publications that are available for download. Other software tools are available such as CHEMKIN [2] and
CANTERA [3].
Flamelets in turbulent combustion
In turbulent flames the interest is 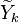 .
In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scale
and obviously is much smaller than the grid size.
It is therefore needed a distribution of the passive scalar within the cell.
.
In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scale
and obviously is much smaller than the grid size.
It is therefore needed a distribution of the passive scalar within the cell.
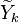 cannot be obtained directly from the flamelets library
cannot be obtained directly from the flamelets library
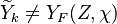 , where
, where 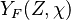 corresponds
to the value obtained from the flamelets libraries.
A generic solution can be expressed as
corresponds
to the value obtained from the flamelets libraries.
A generic solution can be expressed as
where 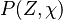 is the joint Probability Density Function (PDF) of the mixture fraction
and scalar dissipation which account for the scalar distribution inside the cell and "a priori"
depends on time and space.
is the joint Probability Density Function (PDF) of the mixture fraction
and scalar dissipation which account for the scalar distribution inside the cell and "a priori"
depends on time and space.
The most simple assumption is to use a constant distribution of the scalar dissipation within the cell and the above equation reduces to
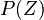 is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a beta PDF)
can be build depending only on two moments of the scalar
mean and variance,
is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a beta PDF)
can be build depending only on two moments of the scalar
mean and variance,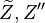 .
.
If the mixture fraction and scalar dissipation are consider independent variables,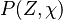 can be written as
can be written as 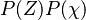 . The PDF of the scalar dissipation is assumed to be log-normal with
variance unity.
. The PDF of the scalar dissipation is assumed to be log-normal with
variance unity.
In Large eddy simulation (LES) context (see #LES equations for reacting flow),
the probability density function is replaced by a subgrid PDF  .
The same equation hold by replacing averaged values with filtered values.
.
The same equation hold by replacing averaged values with filtered values.
The assumptions made regarding the shapes of the PDFs are still justified. In LES combustion the subgrid variance is smaller than RANS counterpart (part of the large-scale fluctuations are solved) and therefore the modelled PDFs are thinner.
Unsteady flamelets
Intrinsic Low Dimensional Manifolds (ILDM)
Detailed mechanisms describing ignition, flame propagation and pollutant formation typically involve several hundred species and elementary reactions, prohibiting their use in practical three-dimensional engine simulations. Conventionally reduced mechanisms often fail to predict minor radicals and pollutant precursors. The ILDM-method is an automatic reduction of a detailed mechanism, which assumes local equilibrium with respect to the fastest time scales identified by a local eigenvector analysis. In the reactive flow calculation, the species compositions are constrained to these manifolds. Conservation equations are solved for only a small number of reaction progress variables, thereby retaining the accuracy of detailed chemical mechanisms. This gives an effective way of coupling the details of complex chemistry with the time variations due to turbulence.
The intrinsic low-dimensional manifold (ILDM) method {Maas:1992,Maas:1993} is a method for in-situ reduction of a detailed chemical mechanism based on a local time scale analysis. This method is based on the fact that different trajectories in state space start from a high-dimensional point and quickly relax to lower-dimensional manifolds due to the fast reactions. The movement along these lower-dimensional manifolds, however, is governed by the slow reactions. It exploits the variety of time scales to systematically reduce the detailed mechanism. For a detailed chemical mechanism with N species, N different time scales govern the process. An assumption that all the time scales are relaxed results in assuming complete equilibrium, where the only variables required to describe the system are the mixture fraction, the temperature and the pressure. This results in a zero-dimensional manifold. An assumption that all but the slowest 'n' time scales are relaxed results in a 'n' dimensional manifold, which requires the additional specification of 'n' parameters (called progress variables). In the ILDM method, the fast chemical reactions do not need to be identified a priori. An eigenvalue analysis of the detailed chemical mechanism is carried out which identifies the fast processes in dynamic equilibrium with the slow processes. The computation of ILDM points can be expensive, and hence an in-situ tabulation procedure is used, which enables the calculation of only those points that are needed during the CFD calculation.
--Fredgauss 07:37, 25 August 2006 (MDT)
U. Maas, S.B. Pope. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Comb. Flame 88, 239, 1992.
Ulrich Maas. Automatische Reduktion von Reaktionsmechanismen zur Simulation reaktiver Str¨omungen. Habilitationsschrift, Universit ¨at Stuttgart, 1993.
Conditional Moment Closure (CMC)
In Conditional Moment Closure (CMC) methods we assume that the species mass fractions are all correlated with the mixture fraction (in non premixed combustion).
From Probability density function we have
where  is the sample space for
is the sample space for  .
.
CMC consists of providing a set of transport equations for the conditional moments which define the flame structure.
Experimentally, it has been observed that temperature and chemical radicals are strong non-linear functions of mixture fraction. For a given species mass fraction we can decomposed it into a mean and a fluctuation:
The fluctuations 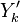 are usually very strong in time and space which makes the closure
of
are usually very strong in time and space which makes the closure
of 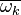 very difficult.
However, the alternative decomposition
very difficult.
However, the alternative decomposition
where 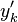 is the fluctuation around the conditional mean or the "conditional fluctuation".
Experimentally, it is observed that
is the fluctuation around the conditional mean or the "conditional fluctuation".
Experimentally, it is observed that 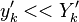 , which forms the basic assumption of the CMC method.
Closures. Due to this property better closure methods can be used reducing the non-linearity
of the mass fraction equations.
, which forms the basic assumption of the CMC method.
Closures. Due to this property better closure methods can be used reducing the non-linearity
of the mass fraction equations.
The Derivation of the CMC equations produces the following CMC transport equation
where 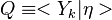 for simplicity.
for simplicity.
In this equation, high order terms in Reynolds number have been neglected. (See Derivation of the CMC equations for the complete series of terms).
It is well known that closure of the unconditional source term
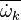 as a function of the
mean temperature and species (
as a function of the
mean temperature and species (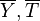 ) will give rise to large errors.
However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.
The first order closure
) will give rise to large errors.
However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.
The first order closure
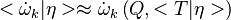 is a good approximation in zones which are not close to extinction.
is a good approximation in zones which are not close to extinction.
Second order closure
A second order closure can be obtained if conditional fluctuations are taken into account.
For a chemical source term in the form 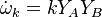 with the rate constant in Arrhenius form
with the rate constant in Arrhenius form
![k=A_0 T^\beta exp [-Ta/T]](/W/images/math/2/e/0/2e0c186caff5787cd5f2f76baac86531.png) the second order closure is (Klimenko and Bilger 1999)
the second order closure is (Klimenko and Bilger 1999)
where 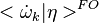 is the first order CMC closure and
is the first order CMC closure and
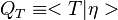 .
When the temperature exponent
.
When the temperature exponent  or
or 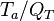 are large the error of taking the first order approximation increases.
Improvement of small pollutant predictions can be obtained using the above reaction
rate for selected species like CO and NO.
are large the error of taking the first order approximation increases.
Improvement of small pollutant predictions can be obtained using the above reaction
rate for selected species like CO and NO.
Double conditioning
Close to extinction and reignition. The conditional fluctuations can be very large
and the primary closure of CMC of "small" fluctuations is not longer valid.
A second variable 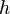 can be chosen to define a double conditioned mass fraction
can be chosen to define a double conditioned mass fraction
Due to the strong dependence on chemical reactions to temperature, 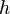 is advised to be a temperature related variable (Kronenburg 2004).
Scalar dissipation is not a good choice, due to its log-normal behaviour
(smaller scales give highest dissipation). A must better choice is the sensible enthalpy
or a progress variable.
Double conditional variables have much smaller conditional fluctuations and allow
the existence of points with the same chemical composition which can be fully burning
(high temperature) or just mixing (low temperature).
The range of applicability is greatly increased and allows non-premixed and premixed problems
to be treated without ad-hoc distinctions.
The main problem is the closure of the new terms involving cross scalar transport.
is advised to be a temperature related variable (Kronenburg 2004).
Scalar dissipation is not a good choice, due to its log-normal behaviour
(smaller scales give highest dissipation). A must better choice is the sensible enthalpy
or a progress variable.
Double conditional variables have much smaller conditional fluctuations and allow
the existence of points with the same chemical composition which can be fully burning
(high temperature) or just mixing (low temperature).
The range of applicability is greatly increased and allows non-premixed and premixed problems
to be treated without ad-hoc distinctions.
The main problem is the closure of the new terms involving cross scalar transport.
The double conditional CMC equation is obtained in a similar manner than the conventional CMC equations
LES modelling
In a LES context a conditional filtering operator can be defined
and 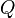 therefore represents a conditionally filtered reactive scalar.
therefore represents a conditionally filtered reactive scalar.
Linear Eddy Model
The Linear Eddy Model (LEM) was first developed by Kerstein(1988). It is an one-dimensional model for representing the flame structure in turbulent flows.
In every computational cell a molecular, diffusion and chemical model is defined as
where 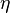 is a spatial coordinate. The scalar distribution obtained can be seen as a
one-dimensional reference field between Kolmogorov scale and grid scales.
is a spatial coordinate. The scalar distribution obtained can be seen as a
one-dimensional reference field between Kolmogorov scale and grid scales.
In a second stage a series of re-arranging stochastic event take place.
These events represent the effects
of a certain turbulent structure of size 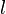 , smaller than the grid size at a location
, smaller than the grid size at a location 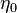 within the one-dimensional domain. This vortex distort the
within the one-dimensional domain. This vortex distort the 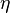 field obtain by the one-dimensional equation,
creating new maxima and minima in the interval
field obtain by the one-dimensional equation,
creating new maxima and minima in the interval 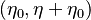 .
The vortex size
.
The vortex size 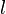 is chosen randomly based on the inertial scale range while
is chosen randomly based on the inertial scale range while
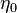 is obtained from a uniform distribution in
is obtained from a uniform distribution in 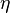 .
The number of events is chosen to match the turbulent diffusivity of the flow.
.
The number of events is chosen to match the turbulent diffusivity of the flow.
PDF transport models
Probability Density Function (PDF) methods are not exclusive to combustion, although they are particularly attractive to them. They provided more information than moment closures and they are used to compute inhomegenous turbulent flows, see reviews in Dopazo (1993) and Pope (1994).
PDF methods are based on the transport equation of the joint-PDF of the scalars.
Denoting 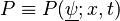 where
where
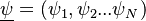 is the phase space for the reactive scalars
is the phase space for the reactive scalars
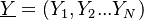 .
The transport equation of the joint PDF is:
.
The transport equation of the joint PDF is:
where the chemical source term is closed. Another term appeared on the right hand side which accounts for the effects of
the molecular mixing on the PDF, is the so called "micro-mixing " term.
Equal diffusivities are used for simplicity 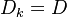
A more general approach is the velocity-composition joint-PDF
with 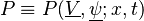 , where
, where
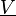 is the sample space of the velocity field
is the sample space of the velocity field
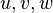 . This approach has the advantage of avoiding gradient-diffusion
modelling. A similar equation to the above is obtained combining the momentum
and scalar transport equation.
. This approach has the advantage of avoiding gradient-diffusion
modelling. A similar equation to the above is obtained combining the momentum
and scalar transport equation.
The PDF transport equation can be solved in two ways: through a Lagrangian approach
using stochastic methods or in a Eulerian ways using stochastic fields.
Lagrangian
The main idea of Lagrangian methods is that the flow can be represented by an ensemble of fluid particles. Central to this approach is the stochastic differential equations and in particular the Langevin equation.
Eulerian
Instead of stochastic particles, smooth stochastic fields can be used to represent the probability density function (PDF) of a scalar (or joint PDF) involved in transport (convection), diffusion and chemical reaction (Valino 1998). A similar formulation was proposed by Sabelnikov and Soulard 2005, which removes part of the a-priori assumption of "smoothness" of the stochastic fields. This approach is purely Eulerian and offers implementations advantages compared to Lagrangian or semi-Eulerian methods. Transport equations for scalars are often easy to programme and normal CFD algorithms can be used (see Discretisation of convective term). Although discretization errors are introduced by solving transport equations, this is partially compesated by the error introduced in Lagrangian approaches due to the numerical evaluation of means.
A new set of 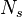 scalar variables
(the stochastic field
scalar variables
(the stochastic field 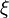 ) is used to represent the
PDF
) is used to represent the
PDF
Other combustion models
MMC
The Multiple Mapping Conditioning (MMC) (Klimenko and Pope 2003) is an extension of the #Conditional Moment Closure (CMC) approach combined with probability density function methods. MMC looks for the minimum set of variables that describes the particular turbulent combustion system.
Fractals
Derived from the #Eddy Dissipation Concept (EDC).
References
[1] Bone, W.A., and Townend, D.T.A. (1927), Flame and Combustion in Gases, Longmans, Green, and Co., Ltd.
[2] (1999), "", Journal of Heat Transfer, Vol. 121, No. 4, pp. 770-73.
[3] Liñan, A. (1974), "The Asymptotic Structure of Counter Flow Diffusion Flames for Large Activation Energies", Acta Astronautica, Vol. 1, No. 7/8, pp. 1007-1039.
- Dopazo, C. (1993), "Recent development in PDF methods", Turbulent Reacting Flows, ed. P. A. Libby and F. A. Williams.
- Fox, R.O. (2003), Computational Models for Turbulent Reacting Flows, ISBN 0-521-65049-6,Cambridge University Press.
- Kerstein, A. R. (1988), "A linear eddy model of turbulent scalar transport and mixing", Comb. Science and Technology, Vol. 60,pp. 391.
- Klimenko, A. Y., Bilger, R. W. (1999), "Conditional moment closure for turbulent combustion", Progress in Energy and Combustion Science, Vol. 25,pp. 595-687.
- Klimenko, A. Y., Pope, S. B. (2003), "The modeling of turbulent reactive flows based on multiple mapping conditioning", Physics of Fluids, Vol. 15, Num. 7, pp. 1907-1925.
- Kronenburg, A., (2004), "Double conditioning of reactive scalar transport equations in turbulent non-premixed flames", Physics of Fluids, Vol. 16, Num. 7, pp. 2640-2648.
- Griffiths, J. F. (1994), "Reduced Kinetic Models and Their Application to Practical Combustion Systems", Prog. in Energy and Combustion Science,Vol. 21, pp. 25-107.
- Peters, N. (2000), Turbulent Combustion, ISBN 0-521-66082-3,Cambridge University Press.
- Poinsot, T.,Veynante, D. (2001), Theoretical and Numerical Combustion, ISBN 1-930217-05-6, R. T Edwards.
- Pope, S. B. (1994), "Lagrangian PDF methods for turbulent flows", Annu. Rev. Fluid Mech, Vol. 26, pp. 23-63.
- Sabel'nikov, V.,Soulard, O. (2005), "Rapidly decorrelating velocity-field model as a tool for solving one-point Fokker-Planck equations for probability density functions of turbulent reactive scalars", Physical Review E, Vol. 72,pp. 016301-1-22.
- Valino, L., (1998), "A field montecarlo formulation for calculating the probability density function of a single scalar in a turbulent flow", Flow. Turb and Combustion, Vol. 60,pp. 157-172.
- Westbrook, Ch. K., Dryer,F. L., (1984), "Chemical Kinetic Modeling of Hydrocarbon Combustion", Prog. in Energy and Combustion Science,Vol. 10, pp. 1-57.

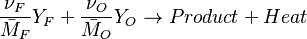
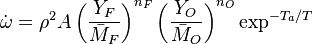
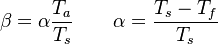
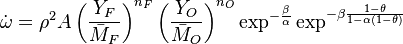
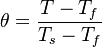
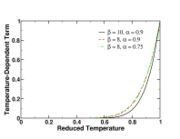
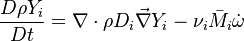
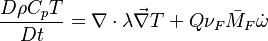
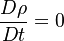
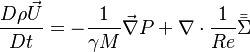
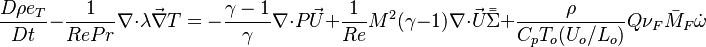
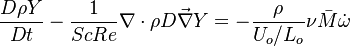
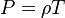
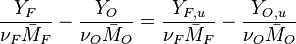
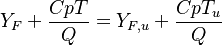
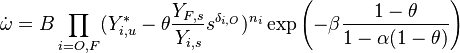
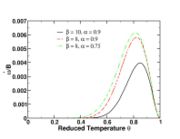

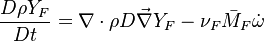
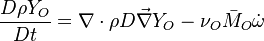
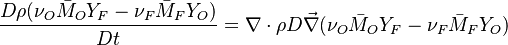
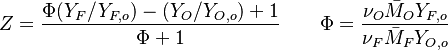
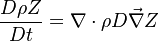
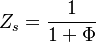
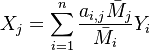
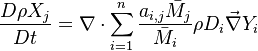
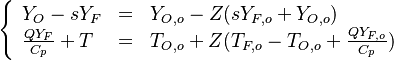
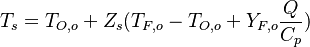
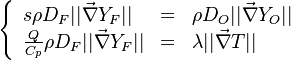
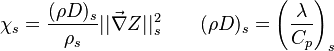

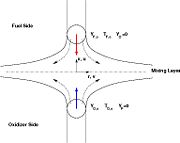
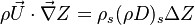
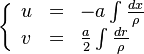
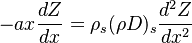
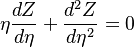
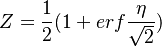
![\chi = \frac{1}{2\pi}\exp\left( - [erf^{-1} (2Z)]^2 \right) \frac{a\rho^2}{\rho_s^2}](/W/images/math/7/a/2/7a2faf8303ce50ef7f33790cbfaab5df.png)
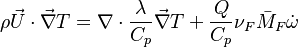
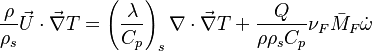
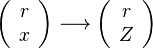
![\left [
\begin{array}{cc}
\frac{\partial r}{\partial r} & \frac{\partial Z}{\partial r} \\
\frac{\partial r}{\partial x} & \frac{\partial Z}{\partial x}
\end{array}\right ] =
\left [
\begin{array}{cc}
1 & 0 \\
0 & (\rho l_d)^{-1}
\end{array}\right ]](/W/images/math/9/9/f/99f373b487a2187521d0f465ec3206f3.png)
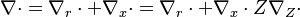
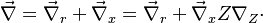
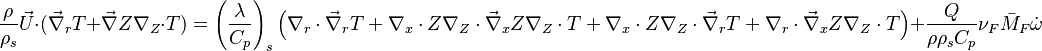
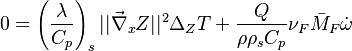
![\int_{Z_s}^{Z} dZ \Delta_Z\phi = \left [\frac{d\phi}{dZ} \right]_{Z_s}^{Z} = - \int_{Z_s}^{Z} dZ Z^{n_F}(1-Z)^{n_O} e^{\phi}{\mathcal D}](/W/images/math/9/f/9/9f95c056d12e9a06cf0f4fb4911c05d5.png)
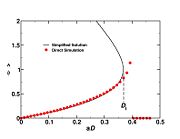
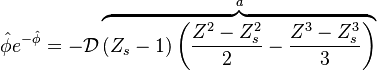
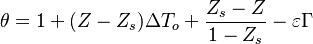
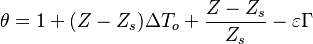
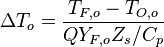
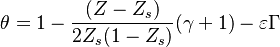
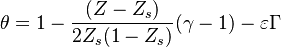
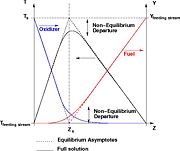
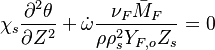
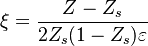
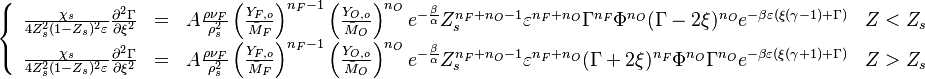
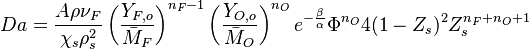
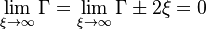
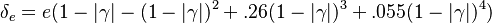
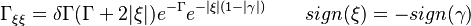
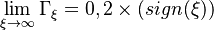
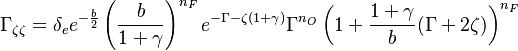
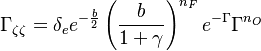
![\left [\frac{\Gamma_{\zeta}}{2}\right ]_{-\infty}^{+\infty} = \delta_e e^{-\frac{b}{2}} \left [\frac{b}{1+\gamma}\right ]^{n_F} \int_{\Gamma(-\infty)}^{\Gamma(+\infty)}d\Gamma e^{-\Gamma} \Gamma^{n_O}](/W/images/math/9/c/e/9ce2667ce51f75a550f0bba3b0661b71.png)
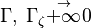
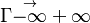
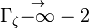
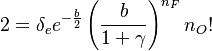
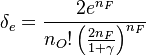
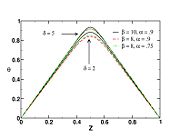
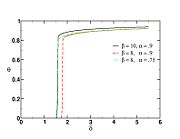
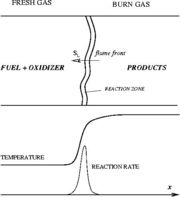
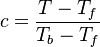
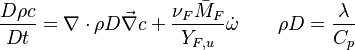
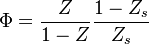
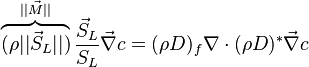
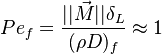
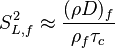
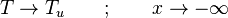
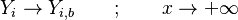
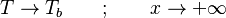
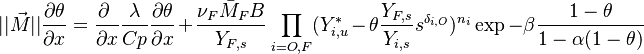
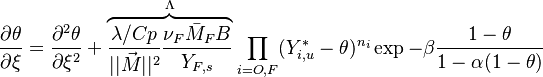
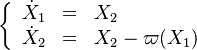
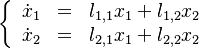
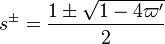
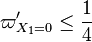
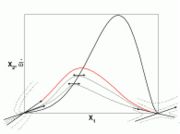
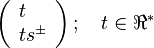
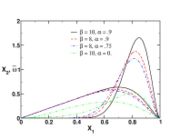
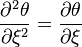
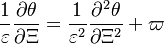
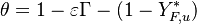
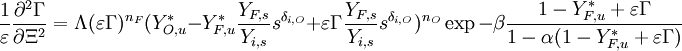

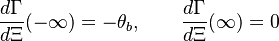
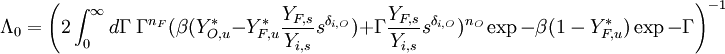
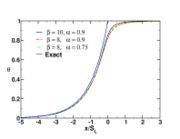
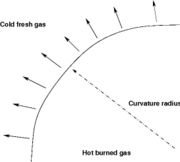
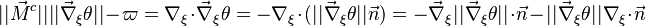
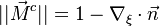
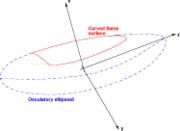
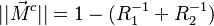
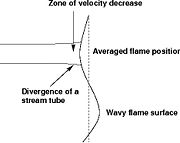
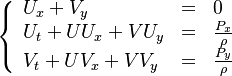
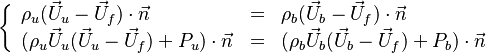
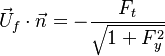
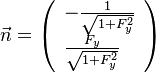
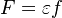
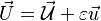
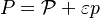
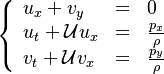
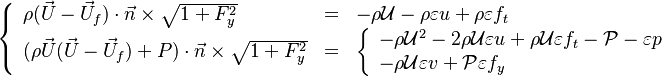
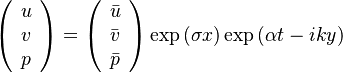
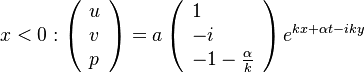
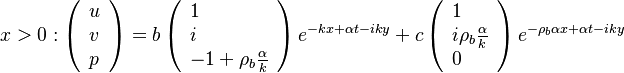
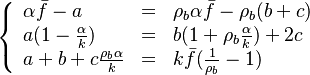
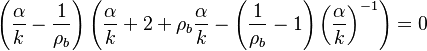
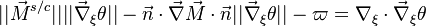
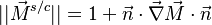
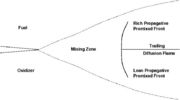
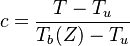
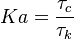
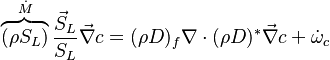
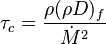
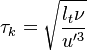
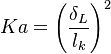
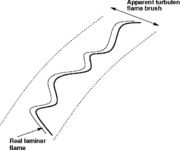
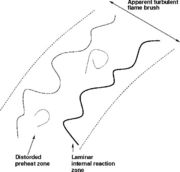
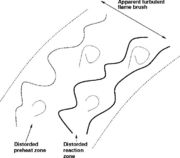
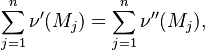
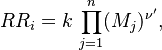
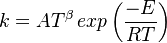
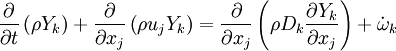
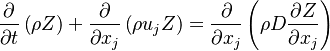
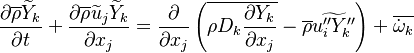
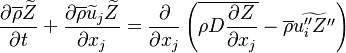
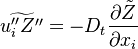
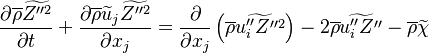
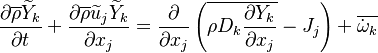
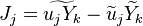
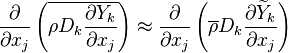
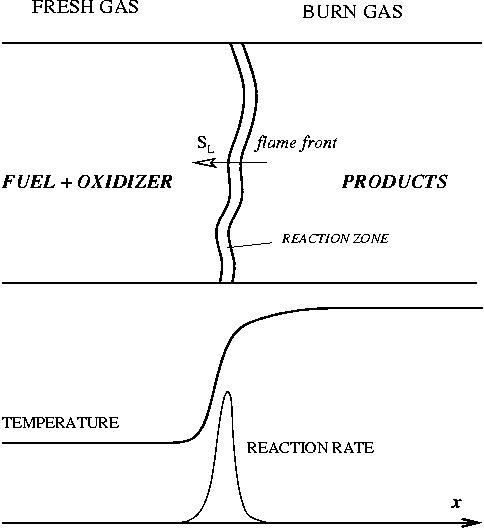
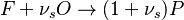
![\bar{\dot\omega}_F=A_{EB} \frac{\epsilon}{k}
min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu},
B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right]](/W/images/math/9/d/6/9d67c48a8dd1f2decb0d5bf3336d215b.png)
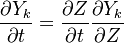
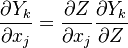
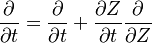
![\rho \frac{\partial Y_k}{\partial t} + Y_k \left[
\frac{\partial \rho}{\partial t} + \frac{\partial \rho u_j}{\partial x_j}
\right]
+ \frac{\partial Y_k}{\partial Z} \left[
\rho \frac{\partial Z}{\partial t} + \rho u_j \frac{\partial Z}{\partial x_j} -
\frac{\partial}{\partial x_j}\left( \rho D \frac{\partial Z}{\partial x_j} \right)
\right]
=
\rho D \left( \frac{\partial Z}{\partial x_j} \frac{\partial Z}{\partial x_j} \right)
\frac{\partial^2 Y_k}{\partial Z^2} + \dot \omega_k](/W/images/math/7/6/9/76972aa831910042bbf0ce5e9610a31b.png)
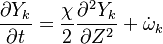
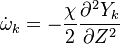
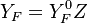
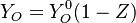
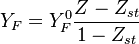
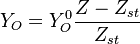
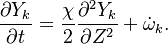
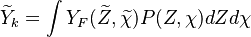
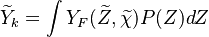
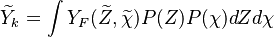
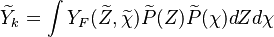
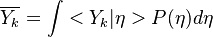
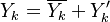
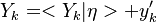
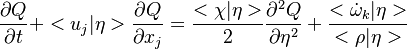
![< \dot \omega_k|\eta> \approx < \dot \omega_k|\eta >^{FO}
\left[1+ \frac{< Y''_A Y''_B |\eta>}{Q_A Q_B}+ \left( \beta + T_a/Q_T \right)
\left(
\frac{< Y''_A T'' |\eta>}{Q_AQ_T} + \frac{< Y''_B T'' |\eta>}{Q_BQ_T}
\right) + ...
\right]](/W/images/math/f/9/c/f9c779360789a63c6bb68e8c13d0489a.png)
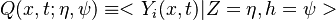
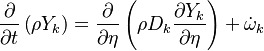
![\frac{\partial <\rho | \underline{Y}=\underline{\psi}> P }{\partial t} + \frac{
\partial <\rho u_j | \underline{Y}=\underline{\psi}> P }{\partial x_j} =
\sum^N_\alpha \frac{\partial}{\partial \psi_\alpha}\left[ \rho \dot{\omega}_\alpha P \right]
- \sum^N_\alpha \sum^N_\beta \frac{\partial^2}{\partial \psi_\alpha \psi_\beta}
\left[ <D \frac{\partial Y_\alpha}{\partial x_i} \frac{\partial Y_\beta}{\partial x_i} | \underline{Y}=\underline{\psi}> \right] P](/W/images/math/1/3/7/13767f4c5947b8df82fdd84c944ea62b.png)
![P (\underline{\psi}; x,t) = \frac{1}{N} \sum^{N_s}_{j=1} \prod^{N}_{k=1} \delta \left[\psi_k -\xi_k^j(x,t) \right]](/W/images/math/f/2/3/f23f3d712f59f83ab17babbfbe9834ab.png)