Detached eddy simulation (DES)
From CFD-Wiki
(→Introduction) |
m (Reverted edits by TroceLbasd (Talk) to last version by Amritkar) |
||
| (2 intermediate revisions not shown) | |||
| Line 6: | Line 6: | ||
</math> | </math> | ||
| - | where <math> C_\hbox{DES} </math> is a constant and <math>\Delta</math> is the largest dimension of the grid cell in question. This modification of the S-A model, while very simple in nature, changes the interpretation of the model substantially. This modified distance function causes the model to behave as a RANS model in regions close to walls, and in a Smagorinsky-like manner away from | + | where <math> C_\hbox{DES} </math> is a constant and <math>\Delta</math> is the largest dimension of the grid cell in question. This modification of the S-A model, while very simple in nature, changes the interpretation of the model substantially. This modified distance function causes the model to behave as a RANS model in regions close to walls, and in a Smagorinsky-like manner away from the walls. This is usually justifed with arguments that the scale-dependence of the model is made local rather than global, and that dimensional analysis backs up this claim. |
The DES approach may be used with any turbulence model that has an appropriately defined turbulence length scale (distance in the S-A model) and is a sufficiently localized model. The [[Baldwin-Barth model]], while very similar to the S-A model, is probably not a candidate for use with DES. The standard version of this model contains several van Driest-type damping functions that make the distance function more global in nature. Menter's SST model [''ref?''] is a good candidate, and has been used by a number of researchers. Menter's SST model uses a turbulence length scale obtained from the model's equations and compares it with the grid length scale to switch between LES and RANS [[#References|[Strelets (2001)]]]. | The DES approach may be used with any turbulence model that has an appropriately defined turbulence length scale (distance in the S-A model) and is a sufficiently localized model. The [[Baldwin-Barth model]], while very similar to the S-A model, is probably not a candidate for use with DES. The standard version of this model contains several van Driest-type damping functions that make the distance function more global in nature. Menter's SST model [''ref?''] is a good candidate, and has been used by a number of researchers. Menter's SST model uses a turbulence length scale obtained from the model's equations and compares it with the grid length scale to switch between LES and RANS [[#References|[Strelets (2001)]]]. | ||
Latest revision as of 09:56, 17 December 2008
Introduction
The difficulties associated with the use of the standard LES models, particularly in near-wall regions, has lead to the development of hybrid models that attempt to combine the best aspects of RANS and LES methodologies in a single solution strategy. An example of a hybrid technique is the detached-eddy simulation (DES) [Spalart et al (1997)] approach. This model attempts to treat near-wall regions in a RANS-like manner, and treat the rest of the flow in an LES-like manner. The model was originally formulated by replacing the distance function 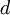 in the Spalart-Allmaras (S-A) model with a modified distance function
in the Spalart-Allmaras (S-A) model with a modified distance function
where 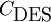 is a constant and
is a constant and 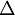 is the largest dimension of the grid cell in question. This modification of the S-A model, while very simple in nature, changes the interpretation of the model substantially. This modified distance function causes the model to behave as a RANS model in regions close to walls, and in a Smagorinsky-like manner away from the walls. This is usually justifed with arguments that the scale-dependence of the model is made local rather than global, and that dimensional analysis backs up this claim.
is the largest dimension of the grid cell in question. This modification of the S-A model, while very simple in nature, changes the interpretation of the model substantially. This modified distance function causes the model to behave as a RANS model in regions close to walls, and in a Smagorinsky-like manner away from the walls. This is usually justifed with arguments that the scale-dependence of the model is made local rather than global, and that dimensional analysis backs up this claim.
The DES approach may be used with any turbulence model that has an appropriately defined turbulence length scale (distance in the S-A model) and is a sufficiently localized model. The Baldwin-Barth model, while very similar to the S-A model, is probably not a candidate for use with DES. The standard version of this model contains several van Driest-type damping functions that make the distance function more global in nature. Menter's SST model [ref?] is a good candidate, and has been used by a number of researchers. Menter's SST model uses a turbulence length scale obtained from the model's equations and compares it with the grid length scale to switch between LES and RANS [Strelets (2001)].
In practice, more programming is needed than simply changing the calculation of the length scale. Many implementations of the DES approach allow for regions to be explicitly designated as RANS or LES regions, overruling the distance function calculation. Also, many implementations use different differencing in RANS regions (e.g. upwinded differences) and LES regions (e.g. central differences).
Computations
Add discusson of results in literature here
References
- Spalart, P. R., Jou, W.-H., Stretlets, M., and Allmaras, S. R. (1997), "Comments on the Feasibility of LES for Wings and on the Hybrid RANS/LES Approach", Advances in DNS/LES, Proceedings of the First AFOSR International Conference on DNS/LES.
- Strelets, M. (2001), "Detached Eddy Simulation of Massively Separated Flows", AIAA 2001-0879.

![\tilde{d}=\min[d,C_\hbox{DES}\Delta],](/W/images/math/6/c/4/6c453f864b43d2aa9e532f47c81d8c47.png)