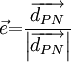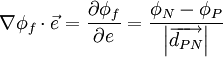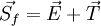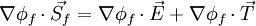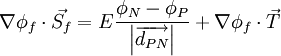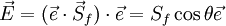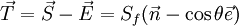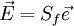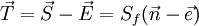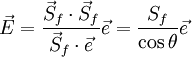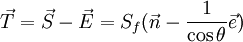Diffusion term
From CFD-Wiki
(difference vector incorrectly defined (compare with picture!)) |
|||
| (One intermediate revision not shown) | |||
| Line 4: | Line 4: | ||
<br> | <br> | ||
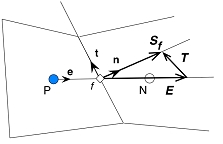
For a general control volume (orthogonal, non-orthogonal), the discretization of the diffusion term can be written in the following form<br> | For a general control volume (orthogonal, non-orthogonal), the discretization of the diffusion term can be written in the following form<br> | ||
| - | <math> \int_{S}\Gamma\nabla\phi\cdot{\rm{d\vec S}} = \sum_{faces}\Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f}} </math> <br> | + | |
| + | :<math> \int_{S}\Gamma\nabla\phi\cdot{\rm{d\vec S}} = \sum_{faces}\Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f}} </math> <br> | ||
where | where | ||
*S denotes the surface area of the control volume | *S denotes the surface area of the control volume | ||
| Line 14: | Line 15: | ||
If <math> \vec r_{P} </math> and <math> \vec r_{N} </math> are position vector of centroids of cells P and N respectively. Then, we define <br> | If <math> \vec r_{P} </math> and <math> \vec r_{N} </math> are position vector of centroids of cells P and N respectively. Then, we define <br> | ||
| - | <math> \overrightarrow{d_{PN}}= \vec r_{ | + | :<math> \overrightarrow{d_{PN}}= \vec r_{N} - \vec r_{P} </math> |
<br> | <br> | ||
| Line 33: | Line 34: | ||
=== Approach 2 === | === Approach 2 === | ||
We define the vector | We define the vector | ||
| - | <math> | + | :<math> |
\vec \alpha {\rm{ = }}\frac{{{\rm{\vec {S_f}}}}}{{{\rm{\vec S_f}} \cdot {\overrightarrow{d_{PN}}}}} | \vec \alpha {\rm{ = }}\frac{{{\rm{\vec {S_f}}}}}{{{\rm{\vec S_f}} \cdot {\overrightarrow{d_{PN}}}}} | ||
</math> | </math> | ||
| Line 45: | Line 46: | ||
=== Orthogonal correction approaches === | === Orthogonal correction approaches === | ||
In non-orthogonal grids, the gradient direction that will yield an expression involving the values at the neighboring control volumes will have to be along the line joining the centroids of the two control volumes. If this direction has a unit vector denoted by <math>\vec e</math> then, by definition <br> | In non-orthogonal grids, the gradient direction that will yield an expression involving the values at the neighboring control volumes will have to be along the line joining the centroids of the two control volumes. If this direction has a unit vector denoted by <math>\vec e</math> then, by definition <br> | ||
| - | <math> | + | :<math> |
\vec e {\rm{ = }} \frac{{{\rm{\overrightarrow{d_{PN}}}}}} {\left| {\overrightarrow{d_{PN}}} \right|} | \vec e {\rm{ = }} \frac{{{\rm{\overrightarrow{d_{PN}}}}}} {\left| {\overrightarrow{d_{PN}}} \right|} | ||
</math><br> | </math><br> | ||
then the gradient in the direction of <math>\vec e</math> can be written as <br> | then the gradient in the direction of <math>\vec e</math> can be written as <br> | ||
| - | <math> \nabla \phi _f \cdot \vec e = \frac {\partial \phi_f} {\partial e} = \frac { \phi_N - \phi_P} {\left| {\overrightarrow{d_{PN}}} \right|} </math> <br> | + | :<math> \nabla \phi _f \cdot \vec e = \frac {\partial \phi_f} {\partial e} = \frac { \phi_N - \phi_P} {\left| {\overrightarrow{d_{PN}}} \right|} </math> <br> |
If the surface vector <math>\vec {S_f}</math> is written as the summation of two vectors <math>\vec {E}</math> and <math>\vec {T}</math> <br> | If the surface vector <math>\vec {S_f}</math> is written as the summation of two vectors <math>\vec {E}</math> and <math>\vec {T}</math> <br> | ||
| - | <math>\vec {S_f} = \vec {E} + \vec {T}</math> <br> | + | :<math>\vec {S_f} = \vec {E} + \vec {T}</math> <br> |
where <math>\vec {E}</math> is in the direction joining the centroids of the two control volumes, we will then be able to express the diffusive flux in terms of the neighboring control volumes plus an additional correction. This is done as follows <br> | where <math>\vec {E}</math> is in the direction joining the centroids of the two control volumes, we will then be able to express the diffusive flux in terms of the neighboring control volumes plus an additional correction. This is done as follows <br> | ||
| - | <math> \nabla \phi_f \cdot \vec {S_f} = \nabla \phi_f \cdot \vec {E} + \nabla \phi_f \cdot \vec {T} </math> <br> | + | :<math> \nabla \phi_f \cdot \vec {S_f} = \nabla \phi_f \cdot \vec {E} + \nabla \phi_f \cdot \vec {T} </math> <br> |
| - | <math> \nabla \phi_f \cdot \vec {S_f} = E \nabla \phi_f \cdot \vec {e} + \nabla \phi_f \cdot \vec {T} </math> .... (where E is the magnitude of <math> \vec E </math><br> | + | :<math> \nabla \phi_f \cdot \vec {S_f} = E \nabla \phi_f \cdot \vec {e} + \nabla \phi_f \cdot \vec {T} </math> .... (where E is the magnitude of <math> \vec E </math><br> |
At the outset, one obtains <br> | At the outset, one obtains <br> | ||
| - | <math> \nabla \phi_f \cdot \vec {S_f} = E \frac { \phi_N - \phi_P} {\left| {\overrightarrow{d_{PN}}} \right|} + \nabla \phi_f \cdot \vec {T} </math> <br> | + | :<math> \nabla \phi_f \cdot \vec {S_f} = E \frac { \phi_N - \phi_P} {\left| {\overrightarrow{d_{PN}}} \right|} + \nabla \phi_f \cdot \vec {T} </math> <br> |
<br> | <br> | ||
The first term in the above equation can be thought of as the orthogonal contribution to the diffusive flux, while the second term represents the non-orthogonal effects. At this point, the vector <math>\vec {T}</math> has not been defined yet. There are three main methods to define this vector. | The first term in the above equation can be thought of as the orthogonal contribution to the diffusive flux, while the second term represents the non-orthogonal effects. At this point, the vector <math>\vec {T}</math> has not been defined yet. There are three main methods to define this vector. | ||
| Line 65: | Line 66: | ||
==== Minimum correction ==== | ==== Minimum correction ==== | ||
In the minimum correction approach, the vectors are defined as <br> | In the minimum correction approach, the vectors are defined as <br> | ||
| - | <math> \vec E = (\vec e \cdot \vec S_f)\cdot \vec e = S_f \cos\theta \vec e </math> <br> | + | :<math> \vec E = (\vec e \cdot \vec S_f)\cdot \vec e = S_f \cos\theta \vec e </math> <br> |
| - | <math> \vec T = \vec S - \vec E= S_f (\vec n - \cos\theta \vec e) </math> <br> | + | :<math> \vec T = \vec S - \vec E= S_f (\vec n - \cos\theta \vec e) </math> <br> |
[[image:Non_orthogonal_CV_minimum_correction.jpg]] <br> | [[image:Non_orthogonal_CV_minimum_correction.jpg]] <br> | ||
'''Minimum Correction Approach''' | '''Minimum Correction Approach''' | ||
| Line 72: | Line 73: | ||
==== Orthogonal correction ==== | ==== Orthogonal correction ==== | ||
In the orthogonal correction approach, the vectors are defined as <br> | In the orthogonal correction approach, the vectors are defined as <br> | ||
| - | <math> \vec E = S_f \vec e </math> <br> | + | :<math> \vec E = S_f \vec e </math> <br> |
| - | <math> \vec T = \vec S - \vec E = S_f (\vec n - \vec e) </math> <br> | + | :<math> \vec T = \vec S - \vec E = S_f (\vec n - \vec e) </math> <br> |
[[image:Non_orthogonal_CV_orthogonal_correction.jpg]] <br> | [[image:Non_orthogonal_CV_orthogonal_correction.jpg]] <br> | ||
'''Orthogonal Correction Approach''' | '''Orthogonal Correction Approach''' | ||
| Line 79: | Line 80: | ||
==== Over relaxed correction ==== | ==== Over relaxed correction ==== | ||
Finally, in the over relaxed approach, we define <br> | Finally, in the over relaxed approach, we define <br> | ||
| - | <math> \vec E = \frac {\vec S_f \cdot \vec S_f}{\vec S_f \cdot \vec e} \vec e = \frac {S_f}{\cos \theta} \vec e </math> <br> | + | :<math> \vec E = \frac {\vec S_f \cdot \vec S_f}{\vec S_f \cdot \vec e} \vec e = \frac {S_f}{\cos \theta} \vec e </math> <br> |
| - | <math> \vec T = \vec S - \vec E = S_f (\vec n - \frac{1}{\cos \theta} \vec e) </math> <br> | + | :<math> \vec T = \vec S - \vec E = S_f (\vec n - \frac{1}{\cos \theta} \vec e) </math> <br> |
[[image:Non_orthogonal_CV_Over_relaxed_correction.jpg]] <br> | [[image:Non_orthogonal_CV_Over_relaxed_correction.jpg]] <br> | ||
'''Over Relaxed Correction Approach''' | '''Over Relaxed Correction Approach''' | ||
Latest revision as of 07:32, 22 January 2010
Contents |
Discretisation of the diffusion term
Description
For a general control volume (orthogonal, non-orthogonal), the discretization of the diffusion term can be written in the following form
where
- S denotes the surface area of the control volume
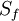 denotes the area of a face for the control volume
denotes the area of a face for the control volume
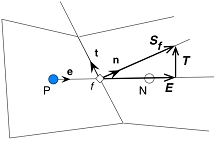
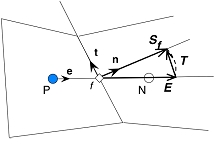
As usual, the subscript f refers to a given face. The figure below describes the terminology used in the framework of a general non-orthogonal control volume
A general non-orthogonal control volume
If  and
and  are position vector of centroids of cells P and N respectively. Then, we define
are position vector of centroids of cells P and N respectively. Then, we define
We wish to approaximate the diffusive flux 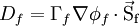 at the face.
at the face.
Approach 1
A first approach is to use a simple expression for estimating the gradient of a scalar normal to the face.
where 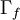 is a suitable face average.
is a suitable face average.
This approach is not very good when the non-orthogonality of the faces increases. If this is the case, it is advisable to use one of the following approaches.
Approach 2
We define the vector
giving us the expression:
where 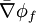 and
and 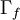 are suitable face averages.
are suitable face averages.
Orthogonal correction approaches
In non-orthogonal grids, the gradient direction that will yield an expression involving the values at the neighboring control volumes will have to be along the line joining the centroids of the two control volumes. If this direction has a unit vector denoted by 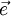 then, by definition
then, by definition
then the gradient in the direction of 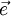 can be written as
can be written as
If the surface vector 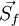 is written as the summation of two vectors
is written as the summation of two vectors 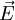 and
and 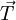
where 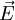 is in the direction joining the centroids of the two control volumes, we will then be able to express the diffusive flux in terms of the neighboring control volumes plus an additional correction. This is done as follows
is in the direction joining the centroids of the two control volumes, we will then be able to express the diffusive flux in terms of the neighboring control volumes plus an additional correction. This is done as follows
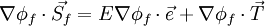 .... (where E is the magnitude of
.... (where E is the magnitude of 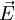
At the outset, one obtains
The first term in the above equation can be thought of as the orthogonal contribution to the diffusive flux, while the second term represents the non-orthogonal effects. At this point, the vector 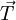 has not been defined yet. There are three main methods to define this vector.
has not been defined yet. There are three main methods to define this vector.
Minimum correction
In the minimum correction approach, the vectors are defined as
Orthogonal correction
In the orthogonal correction approach, the vectors are defined as
Orthogonal Correction Approach
Over relaxed correction
Finally, in the over relaxed approach, we define
Over Relaxed Correction Approach
References
- Ferziger, J.H. and Peric, M. (2001), Computational Methods for Fluid Dynamics, ISBN 3540420746, 3rd Rev. Ed., Springer-Verlag, Berlin..
- Hrvoje, Jasak (1996), "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows", PhD Thesis, Imperial College, University of London (download).
- Darwish, Marwan (2003), "CFD Course Notes", Notes, American University of Beirut.
- Saad, Tony (2005), "Implementation of a Finite Volume Unstructured CFD Solver Using Cluster Based Parallel Computing", Thesis, American University of Beirut.
Return to Numerical Methods

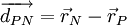
![D_f = \Gamma _f \nabla \phi _f \cdot \vec S_f = \Gamma _f \left[ {\left( {\phi _N - \phi _P } \right)\left| {{{\vec S_f} \over {\overrightarrow{d_{PN}}}}} \right|} \right]](/W/images/math/2/2/f/22f7fe72fd16546ff2d65bf48adf7a35.png)
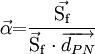
![D_f = \Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _N - \phi _P } \right)\vec \alpha \cdot {\rm{\vec S_f + }}\bar \nabla \phi_f \cdot {\rm{\vec S_f - }}\left( {\bar \nabla \phi_f \cdot {\overrightarrow{d_{PN}}}} \right)\vec \alpha \cdot {\rm{\vec S_f}}} \right]](/W/images/math/7/c/f/7cf1e0cce420c5d8f260ea5c7f3340ff.png)