Discretization of the transient term
From CFD-Wiki
| Line 9: | Line 9: | ||
<math> \frac {\partial (\rho \phi)} {\partial t} V= L(\phi)</math> <br> | <math> \frac {\partial (\rho \phi)} {\partial t} V= L(\phi)</math> <br> | ||
where L denotes the spatial discretization operator, and V denotes the volume. | where L denotes the spatial discretization operator, and V denotes the volume. | ||
| + | (to be continued) | ||
Revision as of 02:56, 8 December 2005
Introduction
To account for transient effects, the governing equations must be discretized in time. As it turns out, the temporal discretization is slightly easier to deal with than that for the spacial effects. Since the governing equation is hyperbolic/parabolic in time, the solution at time t depends upon its history and not on its future. Transient effects are usually dealt with by using a time stepping procedure, with an initial condition provided. The time dimension is divided into a set a discrete time steps, each of size 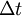 . The solution algorithm therefore marches forward in time, computing a solution at each time step. The spatial discretization for the time-dependent equations is identical to the steady-state case.
. The solution algorithm therefore marches forward in time, computing a solution at each time step. The spatial discretization for the time-dependent equations is identical to the steady-state case.
Temporal discretization involves the integration of every term in the differential equations over the time step 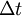 . The integration of transient effects takes several forms each yielding a different accuracy. For simplicity, we express the time dependent transport of a scalar
. The integration of transient effects takes several forms each yielding a different accuracy. For simplicity, we express the time dependent transport of a scalar 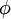 as
as
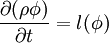
where the function 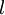 is an operator that incorporates all of the non-transient terms, namely, diffusion, convection, and source terms.
is an operator that incorporates all of the non-transient terms, namely, diffusion, convection, and source terms.
Integrating the above equation over a control volume yields
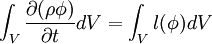
After the spatial dicretization has been performed using the techniques describes in the other sections, we obtain
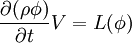
where L denotes the spatial discretization operator, and V denotes the volume.
(to be continued)
